
山东省临沂市沂南县2023-2024学年八年级上学期期末数学试题()
展开注意事项:
1.本试卷共120分.考试时间90分钟.答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、准考证号、座号填写在试卷和答题卡规定的位置.考试结束后,只将答题卡收回.
2.答题注意事项见答题卡,答在本试卷上不得分.
一、选择题(本大题共12小题,每小题3分,共36分)在每小题所给的四个选项中,只有一项是符合题目要求的.
1.使分式有意义的x的取值范围是( )
A.B.C.D.
2.剪纸文化是中国最古老的民间艺术之一,下列剪纸作品中,是轴对称图形的为( )
A.B.C.D.
3.下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cmB.7cm,4cm,2cm
C.10cm,10cm,2cmD.3cm,4cm,8cm
4.下列计算正确的是( )
A.B.C.D.
5.如图1是我国古建筑墙上采用的八角形空窗,其轮廓是一个正八边形,窗外之境如同镶嵌于一个画框之中,如图2是八角形空窗的示意图,它的一个外角∠1的度数为( )
A.45°B.60°C.110°D.135°
6.如果是完全平方式,则m的值为( )
A.-36B.-9C.9D.36
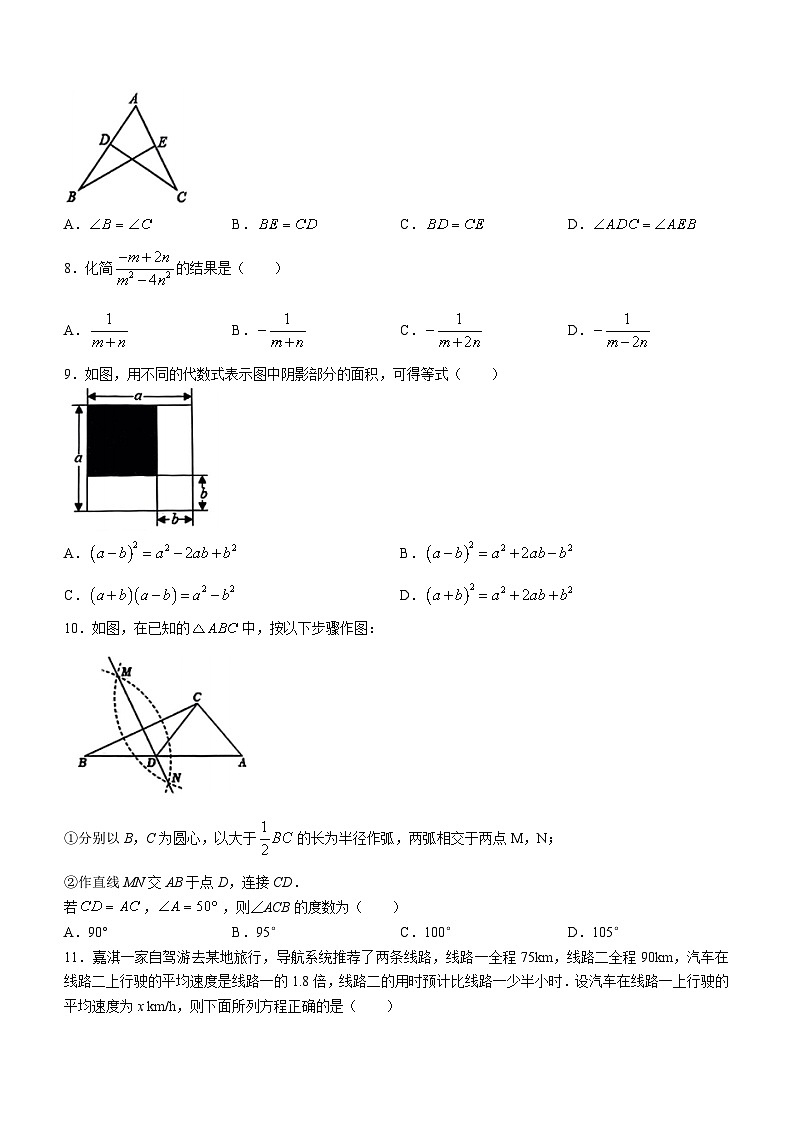
7.如图,,若要使,则添加的一个条件不能是( )
A.B.C.D.
8.化简的结果是( )
A.B.C.D.
9.如图,用不同的代数式表示图中阴影部分的面积,可得等式( )
A.B.
C.D.
10.如图,在已知的中,按以下步骤作图:
①分别以B,C为圆心,以大于的长为半径作弧,两弧相交于两点M,N;
②作直线MN交AB于点D,连接CD.
若,,则∠ACB的度数为( )
A.90°B.95°C.100°D.105°
11.嘉淇一家自驾游去某地旅行,导航系统推荐了两条线路,线路一全程75km,线路二全程90km,汽车在线路二上行驶的平均速度是线路一的1.8倍,线路二的用时预计比线路一少半小时.设汽车在线路一上行驶的平均速度为x km/h,则下面所列方程正确的是( )
A.B.C.D.
12.如图,在中,,,AD平分∠BAC,交AC的延长线于F,垂足为E.则E结论:①;②;③;④;⑤.其中正确结论的个数是( )
A.1B.2C.3D.4
二、填空题(每小题3分,共12分)请将正确的答案填在横线上.
13.在平面直角坐标系中,点关于y轴对称的点的坐标是______.
14.因式分解:______.
15.若分式值为0,则x的值是______.
16.如图,在中,,.垂足为D,BE是的角平分线分别交AD,AC于点P,E.则下列说法:①;②是等边三角形;③;④.其中正确的有______.(写出所有正确的序号)
三、解答题(本大题共7小题,共72分)
17.(本题满分12分)
计算:(1);(2)
18.(本题满分8分)
如图,在中,,,AD为的角平分线.以点A圆心,AD长为半径画弧,与AB,AC分别交于点E,F,连接DE,DF.求∠BDE的度数.
19.(本小题满分8分)
解方程:.
20.(本小题满分10分)
阅读与思考:
教科书中这样写道:“形如的式子称为完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值、最小值等问题.
例如:分解因式:.
解:原式
再如:求代数式的最小值.
解:,
∵,可知当时,有最小值,最小值是-10.
根据阅读材料,用配方法解决下列问题:
(1)分解因式:;
(2)当x为何值时,多项式有最小值?并求出这个最小值.
21.(本小题满分10分)
如图有一块长为米,宽为米的长方形地块,规划部门计划将阴影部分进行绿化,中间将修建一座雕像,左右两边修两条宽为a米的道路.
(1)试用含a,b的代数式表示绿化的面积是多少平方米?
(2)若,,请求出绿化面积.
22.(本小题满分12分)
春节将至,某超市计划购进A,B两类礼盒水果,已知用2000元购进A类礼盒水果的盒数与用1600元购进B类礼盒水果的盒数相同,B类礼盒水果的单价比A类礼盒水果的单价少20元.
(1)求A,B两类礼盒水果的单价各是多少元;
(2)超市计划购进A,B两类礼盒水果共50盒,且购买的总费用不超过4600元,求最多可以购进多少盒A类礼盒水果?
23.(本小题满分12分)
综合与探究:
(1)如图①,C为线段AB上一点,现有,,,,则可以推出,故当,时,AB长为______.
(2)如图②,在等腰直角三角形中,,P为BC边上一点,作分别交AC,AB于点M,N,且,求证:.
(3)如图③,在中,,D,A,E三点共线,且,以AC为边作等边三角形AFC,连接FB,试探究的形状,并说明理由.
山东省临沂市沂南县2023—-2024学年上学期七年级期末数学试题: 这是一份山东省临沂市沂南县2023—-2024学年上学期七年级期末数学试题,共6页。
山东省临沂市沂南县2023-2024学年九年级上学期期中数学试卷: 这是一份山东省临沂市沂南县2023-2024学年九年级上学期期中数学试卷,共25页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
2023年山东省临沂市沂南县中考一模数学试题(含答案解析): 这是一份2023年山东省临沂市沂南县中考一模数学试题(含答案解析),共23页。












