数学九年级下册第1章 二次函数1.4 二次函数与一元二次方程的联系优秀ppt课件

这是一份数学九年级下册第1章 二次函数1.4 二次函数与一元二次方程的联系优秀ppt课件，文件包含湘教版数学九年级下册14《二次函数与一元二次方程的联系》课件pptx、湘教版数学九年级下册14《二次函数与一元二次方程的联系》教案doc等2份课件配套教学资源，其中PPT共29页， 欢迎下载使用。
我们学习了一元一次方程kx+b=0（k≠0）和一次函数y=kx+b（k≠0）后，讨论了它们之间的关系如下：
一元二次方程ax2+bx+c=0（a≠0）和二次函数y=ax2+bx+c（a≠0），它们之间存在怎样的关系呢？
当一次函数中的函数值y=0时，一次函数y=kx+b就转化成了一元一次方程kx+b=0．一次函数kx+b=0（k≠0）的图象与x轴交点的横坐标即为一元一次方程kx+b=0的解．
画二次函数y=x2-2x-3的图象，回答下列问题：
问题1：如图，你能从图象中看出它与x轴的交点吗？
二次函数y=x2-2x-3的图象与x轴的交点坐标分别是（-1，0），（3，0）．
观察图象与x轴的交点坐标，当x=-1时，y=___，即________，也就是说x=-1是一元二次方程_________的一个根．同理，当x=3时，y=0，即x2-2x-3=0，也就是说______是一元二次方程__________的一个根．
问题2：二次函数y=x2-2x-3与一元二次方程x2-2x-3=0有怎样的关系呢？
结论：方程x2-2x-3=0的解就是抛物线y=x2-2x-3与x轴的两个交点的横坐标．因此，抛物线与一元二次方程之间是有密切联系的．即：若抛物线y=ax2+bx+c（a≠0）与x轴的两个不同交点，坐标分别是A(x1，0），B（x2，0），则一元二次方程ax2+bx+c=0（a≠0）有两个不相等的实数根分别是x=x1、x=x2．
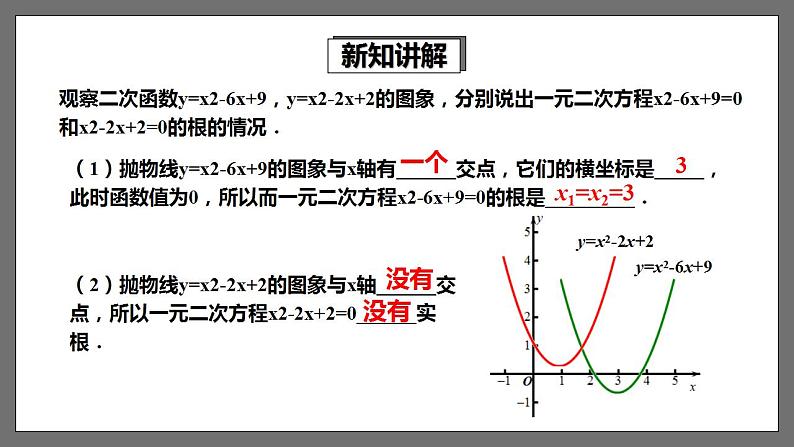
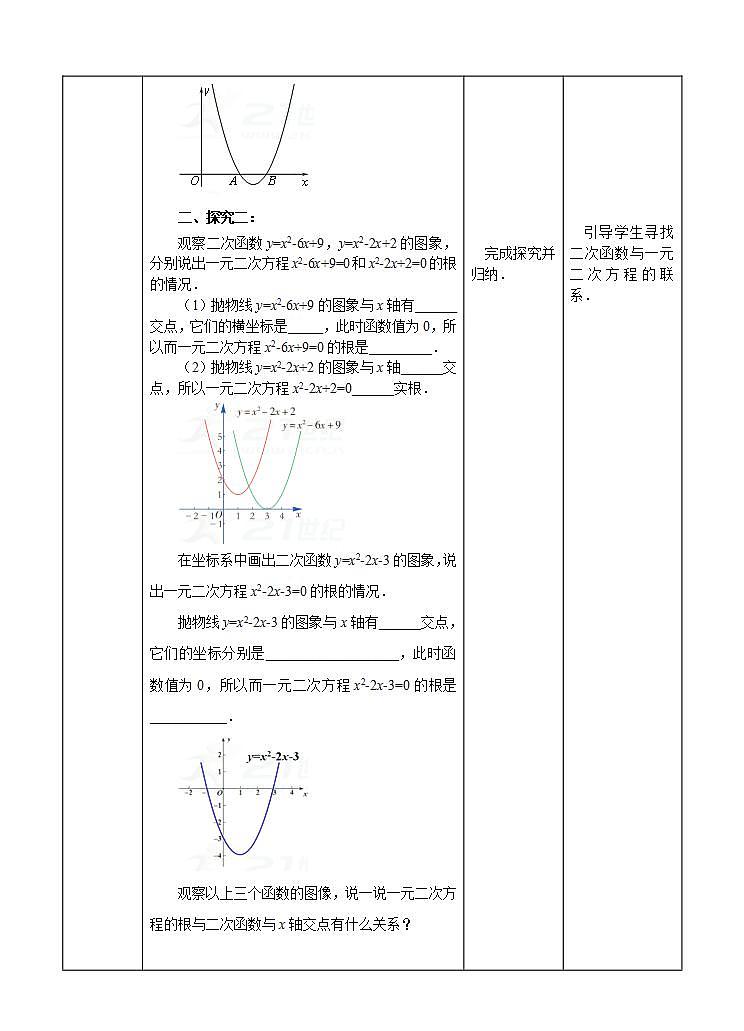
观察二次函数y=x2-6x+9，y=x2-2x+2的图象，分别说出一元二次方程x2-6x+9=0和x2-2x+2=0的根的情况．
（1）抛物线y=x2-6x+9的图象与x轴有______交点，它们的横坐标是_____，此时函数值为0，所以而一元二次方程x2-6x+9=0的根是_________．
（2）抛物线y=x2-2x+2的图象与x轴______交点，所以一元二次方程x2-2x+2=0______实根．
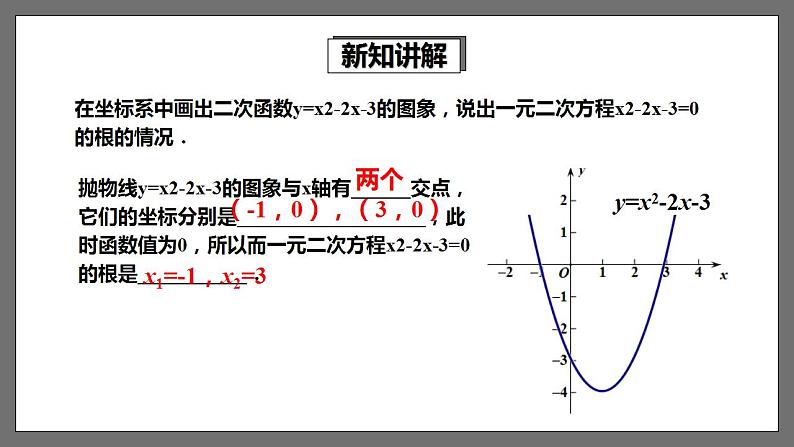
在坐标系中画出二次函数y=x2-2x-3的图象，说出一元二次方程x2-2x-3=0的根的情况．
抛物线y=x2-2x-3的图象与x轴有______交点，它们的坐标分别是___________________，此时函数值为0，所以而一元二次方程x2-2x-3=0的根是___________．
（-1，0），（3，0）
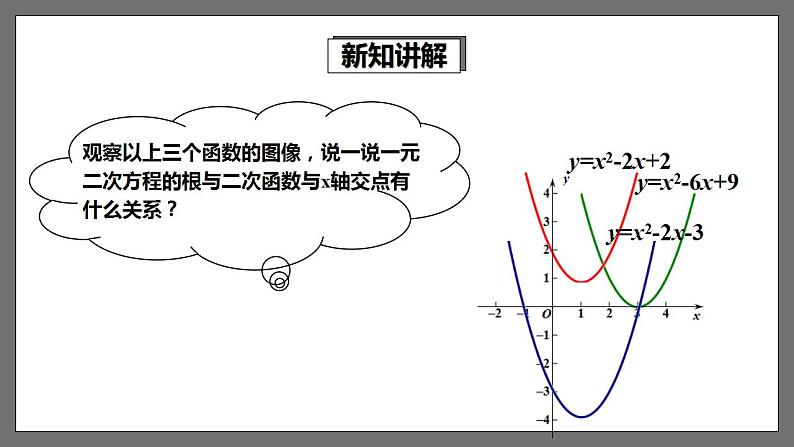
观察以上三个函数的图像，说一说一元二次方程的根与二次函数与x轴交点有什么关系？
一元二次方程的根与二次函数与x轴交点的关系：
求一元二次方程ax2+bx+c=0的根就是求二次函数y=ax2+bx+c在y=0时，自变量x的值，也就是二次函数与x轴交点的横坐标．因而我们可以利用二次函数的图象来求一元二次方程的根．由于作图或观察的误差，由图象求得的根，一般是近似的．
例1 求一元二次方程x2-2x-1=0的根的近似值（精确到0.1）．
解 设二次函数y=x2-2x-1．作出二次y=x2-2x-1的图象，如图．
可以发现抛物线与x轴的一个交点在-1和0之间，另一个交点在2和3之间．
通过观察或测量，可得抛物线与x轴的交点的横坐标约为-0.4或2.4，即一元二次方程x2-2x-1=0的实数根为x1≈-0.4，x2≈2.4．
借助计算器也可以来分析所求方程的实数根．其方法是将二次函数y=x2-2x-1在-1至0范围内的部分x值所对应的y值列表如下：
观察表格可以发现，当x=-0.5时，y=0.25>0；当x=-0.4时，y=-0.04