





湘教版2.4 过不共线三点作圆优秀课件ppt
展开一位考古学家在长沙马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
想一想:要确定一个圆必须满足几个条件?
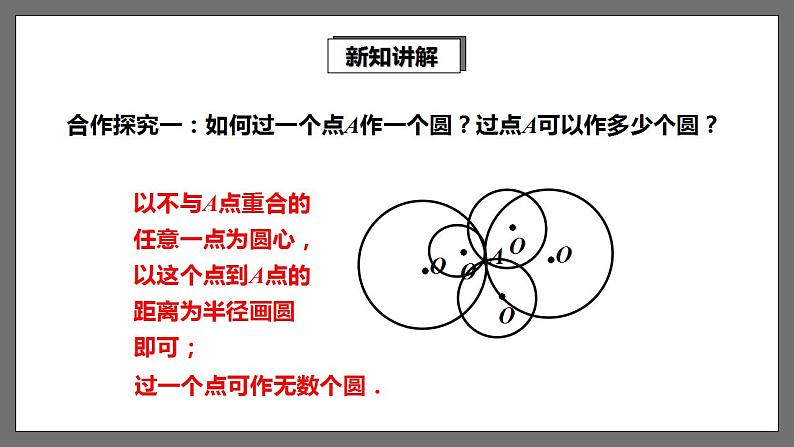
合作探究一:如何过一个点A作一个圆?过点A可以作多少个圆?
以不与A点重合的任意一点为圆心,以这个点到A点的距离为半径画圆即可;
过一个点可作无数个圆.
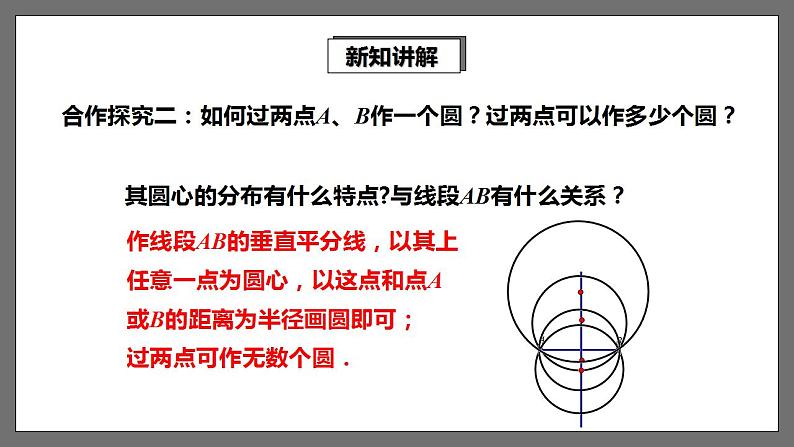
合作探究二:如何过两点A、B作一个圆?过两点可以作多少个圆?
作线段AB的垂直平分线,以其上任意一点为圆心,以这点和点A或B的距离为半径画圆即可;过两点可作无数个圆.
其圆心的分布有什么特点?与线段AB有什么关系?
合作探究三:如何过不在同一直线上的三个点作圆?可以作多少个圆?
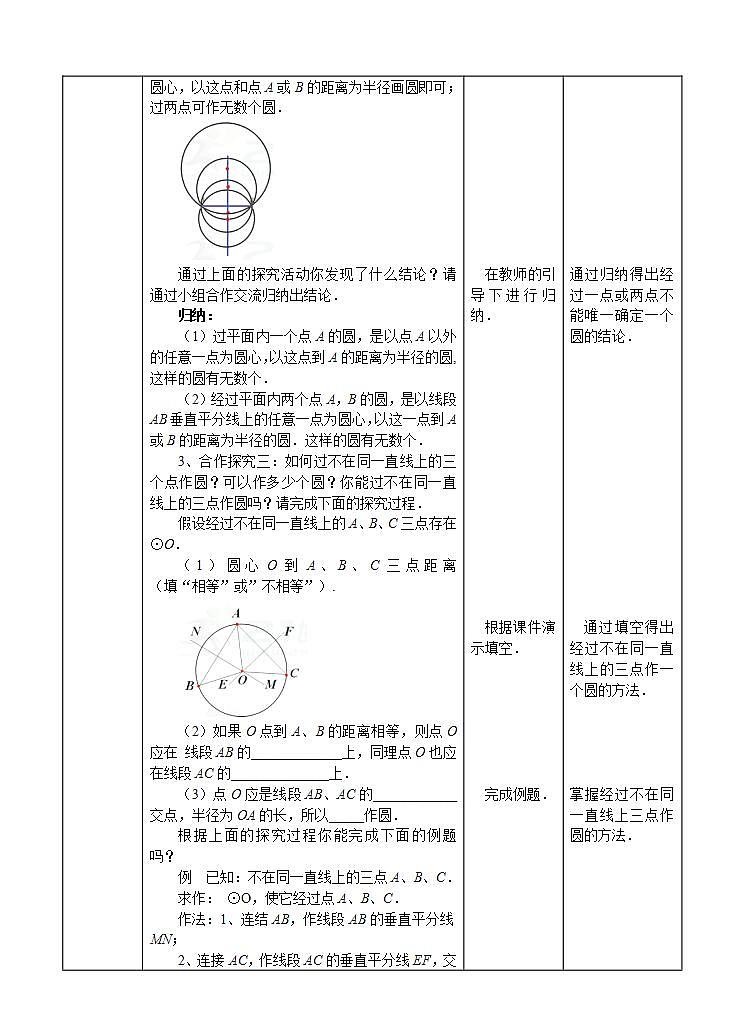
假设经过不在同一直线上的A、B、C三点存在⊙O.
(1)圆心O到A、B、C三点距离 (填“相等”或”不相等”).
(2)如果O点到A、B的距离相等,则点O应在 线段AB的_____________上,同理点O也应在线段AC的______________上.
(3)点O应是线段AB、AC的____________交点,半径为OA的长,所以_____作圆.
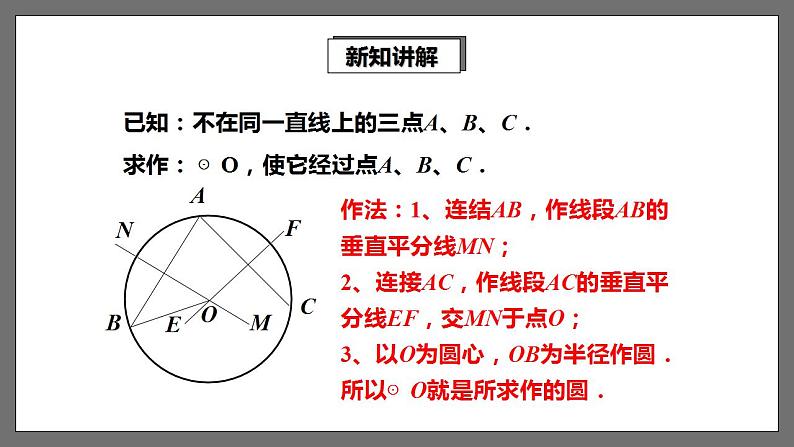
已知:不在同一直线上的三点A、B、C.求作: ⊙O,使它经过点A、B、C.
作法:1、连结AB,作线段AB的垂直平分线MN;2、连接AC,作线段AC的垂直平分线EF,交MN于点O;3、以O为圆心,OB为半径作圆.所以⊙O就是所求作的圆.
结论:经过不在同一直线上的三点可以作一个圆而且只能作一个圆.
过同一直线上的三点A、B、C能作一个圆吗?
经过△ABC的三个顶点可以作一个圆吗?
由于△ABC的三个顶点不在同一直线上,因此过三个顶点可以作唯一一个圆.
经过三角形各顶点的圆叫作这个三角形的外接圆.
☉O叫做△ABC的________, 这个三角形叫作这个圆的内接三角形,△ABC叫做☉O的____________.
定义:三角形外接圆的圆心叫做三角形的外心.
作图:三角形三条边的垂直平分线的交点.
性质:三角形的外心到三角形三个顶点的距离相等.
探究活动四:三角形与它的外心的位置关系.
分别画一个锐角三角形、直角三角形和钝角三角形,再画出它们的外接圆,观察并叙述各三角形与它的外心的位置关系.
锐角三角形的外心位于三角形内;直角三角形的外心位于直角三角形斜边的中点;钝角三角形的外心位于三角形外.
如何将圆形瓷器碎片还原?
方法:1、在圆弧上任取三点A、B、C;2、作线段AB、BC的垂直平分线,其交点O即为圆心;3、以点O为圆心,OC长为半径作圆.⊙O即为所求.
1、三角形的外心具有的性质是( )A.到三边的距离相等 B.到三个顶点的距离相等C.外心在三角形的外 D.外心在三角形内2、小明不慎把家里的圆形镜子打碎了,其中四块碎片如图所示,为了配到与原来大小一样的圆形镜子,小明带到商店去的一块碎片应该是( )A.第一块B.第二块C.第三块D.第四块
3、如图,点 A,B,C均在6×6的正方形网格格点上,过A,B,C三点的外接圆除经过A,B,C三点外还能经过的格点数为5_________.
4、如图所示,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.已知:AB=24 cm,CD=8 cm. (1)求作此残片所在的圆(不写作法,保留作图痕迹); (2)求(1)中所作圆的半径.
解:(1)作弦AC的垂直平分线与弦AB的垂直平分线交于O点,以O为圆心OA长为半径作圆O就是此残片所在的圆,如图.
(2)连接OA,设OA=x,AD=12 cm,OD=(x-8)cm, 则根据勾股定理列方程: x2=122+(x-8)2, 解得:x=13. 答:圆的半径为13 cm .
5、如图,△ABC内接于⊙O,∠B=30°,AC=2 cm,求⊙O的半径.
解:连接OA、OC,如图所示:
∵∠B=30°,∴∠AOC=60°,
∵OA=OC,∴△AOC是等边三角形,
6、如图所示,锐角△ABC,∠A=60°,其外接圆的半径为3,求BC.
解:如图,作直径CD,连接BD,
∵同弧所对的圆周角相等,∴∠BDC=∠BAC=60°.
又∵CD是直径,∴CD=6,∴∠DBC=90°,BD=3,
过两点可以作无数个圆.圆心在以已知两点为端点的线段的垂直平分线上.
过不在同一条直线上的三点确定一个圆.
外心、三角形外接圆、圆的内接三角形.
过在同一条直线上的三点不能作圆.
初中数学湘教版七年级上册2.4 整式优质课课件ppt: 这是一份初中数学湘教版七年级上册2.4 整式优质课课件ppt,共31页。PPT课件主要包含了学习目标,创设情境,探究新知,练一练,判断单项式的方法,方法总结,归纳总结,常数项,多项式的项,多项式的次数等内容,欢迎下载使用。
初中数学湘教版九年级下册2.4 过不共线三点作圆精品课件ppt: 这是一份初中数学湘教版九年级下册2.4 过不共线三点作圆精品课件ppt,文件包含24过不共线三点作圆课件ppt、24过不共线三点作圆教案doc等2份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
初中数学湘教版九年级下册2.4 过不共线三点作圆习题课件ppt: 这是一份初中数学湘教版九年级下册2.4 过不共线三点作圆习题课件ppt,共23页。













