北师大版七年级数学下册高频考点专题突破 期中押题测试卷（考试范围：第一-三章）-【高频考点】（原卷版+解析）

这是一份北师大版七年级数学下册高频考点专题突破 期中押题测试卷（考试范围：第一-三章）-【高频考点】（原卷版+解析），共26页。试卷主要包含了若，则____．，5倍，求、两站相距的路程；等内容，欢迎下载使用。
注意事项：
本试卷满分120分，考试时间90分钟，试题共26题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2021·广东东莞·七年级期末）如图所示，下列四个选项中不正确的是（ ）
A．与是同旁内角 B．与是内错角 C．与是对顶角 D．与是邻补角
2．（2021·深圳市高级中学初二月考）已知：如图，，则，，之间的关系是
A． B． C． D．
3．（2021·山西期末）如图，点，，分别在的边，，上，连接，，在下列给出的条件中，不能判定的是（ ）
A．° B． C． D．
4．（2021·沈阳市第一二七中学期中）若a≠0，化简下列各式，正确的个数有（ ）
（1）a0•a•a5＝a5；（2）（a2）3＝a6；（3）（﹣2a4）3＝﹣6a12；（4）a÷a﹣2＝a3；（5）a6＋a6＝2a12；（6）2﹣2÷25×28＝32；（7）a2•（﹣a）7•a11＝﹣a20
A．1个B．2个C．3个D．4个
5．（2021·广东高州·七年级期末）根据市卫生防疫部门的要求，游泳池必须定期换水后才能对外开放，在换水时需要经排水﹣清洗﹣注水的过程，某游泳馆从早上8：00开始对游泳池进行换水，已知该游泳池共蓄水2500m3，打开放水闸门匀速放水后，游泳池里的水量和放水时间的关系如表，下面说法不正确的是( )
A．每分钟放水20 m3B．游泳池中的水量是因变量，放水时间是自变量
C．放水10分钟时，游泳池中的水量为2300 m3D．游泳池中的水全部放完，需要124分钟
6．（2021·广西象州·七年级期中）利用平方差公式计算的结果是（ ）
A．B．C．D．
7．（2021·宜兴市北郊中学初二期中）如图a是长方形纸带，∠DEF=26°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（ ）
A．102°B．108°C．124°D．128°
8．（2021·天津南开·七年级期末）已知，那么的值为（ ）．
A．5B．1C．10D．2
9．（2021·郑州枫杨外国语学校七年级月考）已知（m﹣53）（m﹣47）＝25，则（m﹣53）2+（m﹣47）2的值为（ ）
A．136B．86C．36D．50
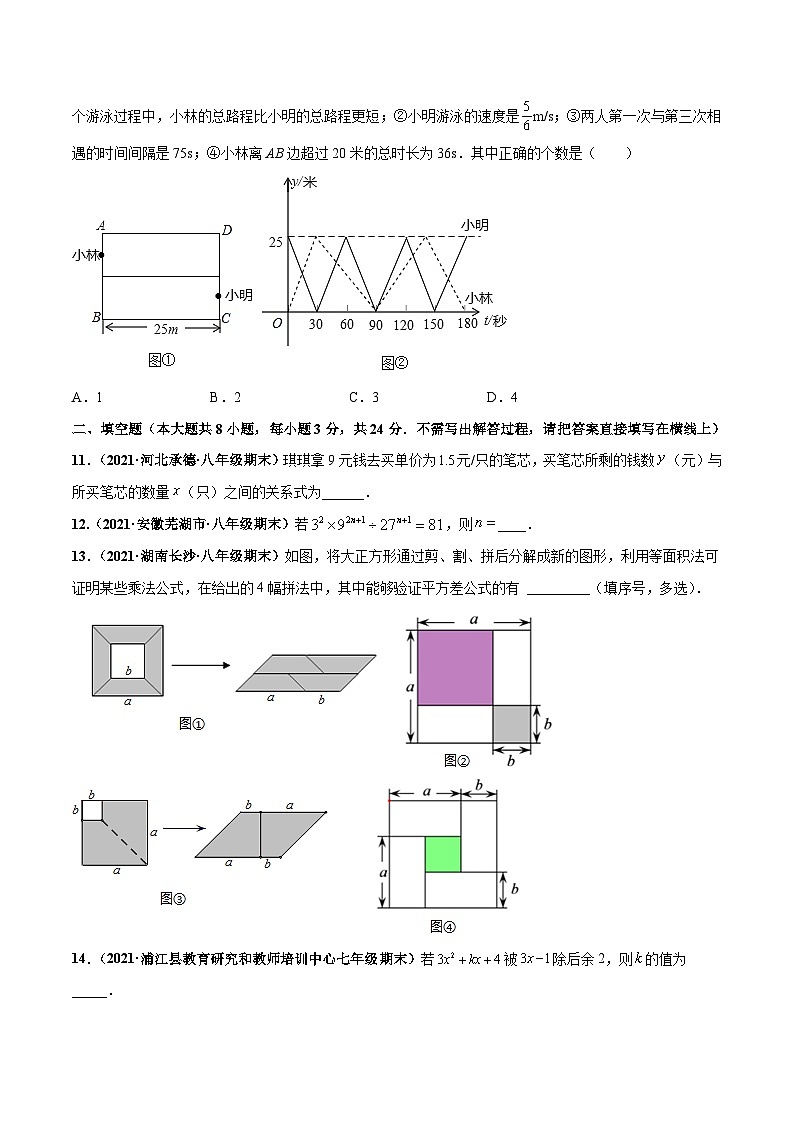
10．（2021·重庆实验外国语学校九年级月考）如图1，某游池长25米，小林和小明两个人分别在游泳池的AB和CD两边，同时朝着另一边以各自的速度匀速游泳，他们游泳的时间为t（s），其中0≤t≤180，到AB边距离为y（m），图2中的实线和虚线分别表示小林和小明在游泳过程中y与t的对应关系，以下推断：①在整个游泳过程中，小林的总路程比小明的总路程更短；②小明游泳的速度是m/s；③两人第一次与第三次相遇的时间间隔是75s；④小林离AB边超过20米的总时长为36s．其中正确的个数是（ ）
A．1B．2C．3D．4
二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在横线上）
11．（2021·河北承德·八年级期末）琪琪拿9元钱去买单价为元/只的笔芯，买笔芯所剩的钱数（元）与所买笔芯的数量（只）之间的关系式为______．
12.（2021·安徽芜湖市·八年级期末）若，则____．
13．（2021·湖南长沙·八年级期末）如图，将大正方形通过剪、割、拼后分解成新的图形，利用等面积法可证明某些乘法公式，在给出的4幅拼法中，其中能够验证平方差公式的有 _________（填序号，多选）．
14．（2021·浦江县教育研究和教师培训中心七年级期末）若被除后余2，则的值为_____．
15．（2021·广东佛山市七年级期中）如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠AED′=30°，则∠BFC′的度数为_________．
16．（2021·湖北武汉·八年级期末）若a＝x＋20，b＝x＋19，c＝x＋21，则a2＋b2＋c2－ab－bc－ac＝______．
17．（2021秋•徐汇区校级期末）某空军加油飞机接到命令，立即给另一架正在飞行的运输机进行空中加油．在加油过程中，设运输飞机的油箱余油量为Q1吨，加油飞机的加油箱余油量为Q2吨，加油时间为t（分），Q1、Q2与t之间的函数图象如图所示，结合图象回答下列问题：
（1）加油之前，加油飞机的加油油箱中装载了 吨油；运输飞机的油箱有余油量 吨油；
（2）这些油全部加给运输飞机需 分钟；（3）运输飞机的飞行油耗为每分钟 吨油；
（4）运输飞机加完油后，以原速继续飞行，如果每分钟油耗相同，最多能飞行 小时．
18．（2021·湖北洪山·七年级期中）如图，已知AB∥CD，P为直线AB，CD外一点，BF平分∠ABP，DE平分∠CDP，BF的反向延长线交DE于点E，若∠FED＝a，试用a表示∠P为______．
三、解答题（本大题共8小题，共66分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（2021·重庆实验外国语学校七年级期中）先化简，再求值：[（x+3y）2﹣（x﹣3y）2﹣（3y﹣x）（x+3y）﹣x2]÷（3y），其中x，y满足x2+4x+4+|y+1|＝0．
20．（2021·江苏南京钟英中学）若（且，m、n是正整数），则．利用上面结论解决下面的问题：（1）如果，求x的值；（2）如果，求x的值；
（3）若，，用含x的代数式表示y．
21．（2021·广西象州·七年级期中）阅读材料，解决问题．
材料一：比较和的大小．
解：因为，而，所以，即．
小结：在指数相同的情况下，可通过比较底数的大小，来确定两个幂的大小．
材料二：比较和的大小．
解：因为，而，所以，即．
小结：在底数相同的情况下，可以通过比较指数的大小，来确定两个幂的大小．
（1）比较，，的大小：（2）比较，，的大小．
22．（2021·福建省永春第一中学八年级月考）上数学课时，王老师在讲完乘法公式（a±b）2＝a2±2ab+b2的多种运用后，要求同学们运用所学知识解答：求代数式x2+4x+5的最小值？同学们经过交流、讨论，最后总结出如下解答方法：
解：x2+4x+5＝x2+4x+4+1＝（x+2）2+1
∵（x+2）2≥0，∴当x＝﹣2时，（x+2）2的值最小，最小值是0，
∴（x+2）2+1≥1∴当（x+2）2＝0时，（x+2）2+1的值最小，最小值是1，
∴x2+4x+5的最小值是1．
请你根据上述方法，解答下列各题
（1）知识再现：当x＝ 时，代数式x2﹣6x+12的最小值是 ；
（2）知识运用：若y＝﹣x2+2x﹣3，当x＝ 时，y有最 值（填“大”或“小”），这个值是 ；
（3）知识拓展：若﹣x2+3x+y+5＝0，求y+x的最小值．
23．（2021·无锡市天一实验学校七年级期中）（知识生成）通常情况下，用两种不同的方法计算同一图形的面积，可以得到一个恒等式．
（1）如图1，根据图中阴影部分（4个完全相同的小长方形）的面积可以得到的等式是： ．
（知识迁移）类似地，用两种不同的方法计算同一几何体的情况，也可以得到一个恒等式．如图2是边长为a+b的正方体，被如图所示的分割成8块．
（2）用不同的方法计算这个正方体的体积，就可以得到一个等式，这个等式可以为： ．
（3）已知a+b=3，ab=1，利用上面的规律求的值．
24．（2021·河南驻马店市·七年级期末）已知：△ABC和平面内一点D．
（1）如图1，点D在BC边上，过D点作DE//BA交AC于点E，作DF//CA交AB于点F，判断∠EDF与∠A的数量关系，并说明理由．（2）如图2，点D在BC的延长线上，DF//CA，∠EDF＝∠A，请你判断DE与BA的位置关系．并说明理由． （3）如图3，点D在△ABC的外部，若作DE//BA，DF//CA，请直接写出∠EDF与∠A数量关系．
25．（2021·浙江温岭·八年级期末）公交公司员工小明住在站点的员工宿舍，每天早上去站点上班，站到站唯一一条公交线路示意图如图1，、、、是四个公交站点，其中、两站相距的路程是1200米，为了健身，小明往往沿公交线路步行到站或站后再乘公交车上班．
（1）星期一，小明步行到站上车，记他距站的路程为米，离开站的时间为分，关于的函数图象如图2，求的解析式及公交车的速度；
（2）星期二，小明以与星期一相同出发时间和步行速度步行到站上车，已知公交车无论上行（→）还是下行（→）都每隔10分钟一班，每天始发时间和行车速度保持不变，乘客上下车时间忽略不计；
①通过计算判断小明步行到达站时是否恰好有上行公交车到达站；
②小明到达站所用时间是星期一的1.5倍，求、两站相距的路程；
③若小明步行至站时刚好遇见一辆下行班车，这一趟上班途中，直接写出他遇到下行班车的最短间隔时间．
26．（2021·湖北十堰·七年级期末）已知ABCD，点E、F分别在AB、CD上，点G为平面内一点，连接EG、FG． （1）如图1，当点G在AB、CD之间时，请直接写出∠AEG、∠CFG与∠G之间的数量关系 ；（2）如图2，当点G在AB上方时，且∠EGF＝90°，求证：∠BEG –∠DFG＝90°；
（3）如图3，在（2）的条件下，过点E作直线HK交直线CD于K，使∠HEG与∠GEB互补，∠EKD的平分交与直线GE交于点L，请你判断FG与KL的位置关系，并证明．
放水时间(分钟)
1
2
3
4
…
游泳池中的水量(m3)
2480
2460
2440
2420
…
期中押题测试卷（考试范围：第一-三章）
姓名：__________________ 班级：______________ 得分：_________________
注意事项：
本试卷满分120分，考试时间90分钟，试题共26题．答卷前，考生务必用0.5毫米黑色签字笔将自己的姓名、班级等信息填写在试卷规定的位置．
一、选择题（本大题共10小题，每小题3分，共30分）在每小题所给出的四个选项中，只有一项是符合题目要求的．
1．（2021·广东东莞·七年级期末）如图所示，下列四个选项中不正确的是（ ）
A．与是同旁内角 B．与是内错角 C．与是对顶角 D．与是邻补角
【答案】B
【分析】根据同旁内角，内错角，对顶角，邻补角的定义逐项分析．
【详解】A. 与是同旁内角，故该选项正确，不符合题意；
B. 与不是内错角，故该选项不正确，符合题意；
C. 与是对顶角，故该选项正确，不符合题意；
D. 与是邻补角，故该选项正确，不符合题意；故选B．
【点睛】本题考查了同旁内角，内错角，对顶角，邻补角的定义，理解定义是解题的关键．两条直线被第三条直线所截,如果两个角分别在两条直线的同侧,且在第三条直线的同旁,那么这两个角叫做同位角．两条直线被第三条直线所截,如果两个角分别在两条直线之间,且在第三条直线的两侧,那么这两个角叫做内错角．两条直线被第三条直线所截,如果两个角分别在两条直线之间,且在第三条直线的同旁,那么这两个角叫做同旁内角．两个角有一条公共边，它们的另一边互为反向延长线，具有这种关系的两个角，互为邻补角．
2．（2021·深圳市高级中学初二月考）已知：如图，，则，，之间的关系是
A． B． C． D．
【答案】C
【分析】分别过C、D作AB的平行线CM和DN，由平行线的性质可得到∠α+∠β=∠C+∠γ，可求得答案．
【解析】解：如图，分别过C、D作AB的平行线CM和DN，
，，，，，
，
又，，，即，故选C．
【点睛】本题主要考查平行线的性质，掌握平行线的判定和性质是解题的关键，即①两直线平行⇔同位角相等，②两直线平行⇔内错角相等，③两直线平行⇔同旁内角互补，④a//b，b//c⇒a//c．
3．（2021·山西期末）如图，点，，分别在的边，，上，连接，，在下列给出的条件中，不能判定的是（ ）
A．° B． C． D．
【答案】B
【分析】据平行线的判定方法结合图形逐选项分析，找出正确选项．
【解析】由，得∠A,∠2互补；由图得∠A,∠2是与AB、DF有关的同旁内角，据同旁内角互补，两直线平行得A选项能判定AB∥DF；
由，得∠A,∠1相等；由图得∠A、∠1是与AC、DE有关的同位角，据同位角相等补，两直线平行得B选项能判定AC∥DE，不能判断AB∥DF；
由，得∠1,∠4相等；由图得∠1、∠4是与AB、DF有关的内错角，据内角角相等，两直线平行得C选项能判定AB∥DF；
由，得∠A,∠3相等；由图得∠A,∠3是与AB、DF有关同位角，据同位角相等，两直线平行得C选项能判定AB∥DF．
综上分析，只有B选项不能判定AB∥DF．故选：B．
【点睛】本题考查平行线的判定．其关键是找准与要判定平行的直线有关的同位角、内错角、同旁内角，再判断它们相等或互补与否才能应用相关判定方法进行判定．
4．（2021·沈阳市第一二七中学期中）若a≠0，化简下列各式，正确的个数有（ ）
（1）a0•a•a5＝a5；（2）（a2）3＝a6；（3）（﹣2a4）3＝﹣6a12；（4）a÷a﹣2＝a3；（5）a6＋a6＝2a12；（6）2﹣2÷25×28＝32；（7）a2•（﹣a）7•a11＝﹣a20
A．1个B．2个C．3个D．4个
【答案】C
【分析】分别根据零整数指数幂的定义，同底数幂的乘除法法则，幂的乘方与积的乘方运算法则，合并同类项法则以及负整数指数幂的定义逐一判断即可．
【解析】解：a0•a•a5＝a6，故（1）错误；（a2）3＝a6，故（2）正确；（﹣2a4）3＝﹣8a12，故（3）错误；
a÷a﹣2＝a3，故（4）正确；a6＋a6＝2a6，故（5）错误；2﹣2÷25×28＝2，故（6）错误；
a2•（﹣a）7•a11＝﹣a20，故（7）正确，所以正确的个数为3个．故选：C．
【点睛】本题考查零整数指数幂的定义，同底数幂的乘除法法则，幂的乘方与积的乘方运算法则，合并同类项法则以及负整数指数幂等知识，熟练掌握法则是关键．
5．（2021·广东高州·七年级期末）根据市卫生防疫部门的要求，游泳池必须定期换水后才能对外开放，在换水时需要经排水﹣清洗﹣注水的过程，某游泳馆从早上8：00开始对游泳池进行换水，已知该游泳池共蓄水2500m3，打开放水闸门匀速放水后，游泳池里的水量和放水时间的关系如表，下面说法不正确的是( )
A．每分钟放水20 m3B．游泳池中的水量是因变量，放水时间是自变量
C．放水10分钟时，游泳池中的水量为2300 m3D．游泳池中的水全部放完，需要124分钟
【答案】D
【分析】据该游泳池共蓄水2500m3与每分钟后游泳池中的剩余水量可得，每分钟放水20m3，继而判断正误．
【详解】解：A．由表格可得每分钟放水20m3，正确．
B．游泳池中的水量随放水时间变化而变化，故放水时间是自变量，游泳池中的水量是因变量，正确．
C．放水十分钟后，剩余水量2500﹣20×10＝2300（m3），正确．
D．全部放完需要2500÷20＝125（分钟），错误．故选：D．
【点睛】本题主要考查变量的表示方法：表格法，另外还有图象法和解析式法，解题关键是从实际应用中构建变量模型求解．
6．（2021·广西象州·七年级期中）利用平方差公式计算的结果是（ ）
A．B．C．D．
【答案】C
【分析】把每个因式逆用平方差公式分解，然后根据乘法结合率和有理数的乘法计算即可．
【详解】解：
=
===故选C．
【点睛】本题考查了平方差公式的运用，熟练掌握平方差公式是解题的关键．
7．（2021·宜兴市北郊中学初二期中）如图a是长方形纸带，∠DEF=26°，将纸带沿EF折叠成图b，再沿BF折叠成图c，则图c中的∠CFE的度数是（ ）
A．102°B．108°C．124°D．128°
【答案】A
【分析】先由矩形的性质得出∠BFE=∠DEF=26°，再根据折叠的性质得出∠CFG=180°-2∠BFE，∠CFE=∠CFG-∠EFG即可．
【解析】∵四边形ABCD是矩形，∴AD∥BC，∴∠BFE=∠DEF=26°，
∴∠CFE=∠CFG-∠EFG=180°-2∠BFE-∠EFG=180°-3×26°=102°，故选：A．
【点睛】本题考查了翻折变换（折叠问题）、矩形的性质、平行线的性质；熟练掌握翻折变换和矩形的性质，弄清各个角之间的关系是解决问题的关键．
8．（2021·天津南开·七年级期末）已知，那么的值为（ ）．
A．5B．1C．10D．2
【答案】B
【分析】由题意易得，进而可得，然后问题可求解．
【详解】解：∵，∴，即，
∴，即，∴，∴；故答案为B．
【点睛】本题主要考查幂的乘方及积的乘方的逆用，熟练掌握幂的乘方及积的乘方是解题的关键．
9．（2021·郑州枫杨外国语学校七年级月考）已知（m﹣53）（m﹣47）＝25，则（m﹣53）2+（m﹣47）2的值为（ ）
A．136B．86C．36D．50
【答案】B
【分析】根据完全平方公式进行变形，可得出答案．
【详解】解：设a=m-53，b=m-47，则ab=25，a-b=-6，
∴a2+b2=（a-b）2+2ab=（-6）2+50=86，∴（m-53）2+（m-47）2=86，故选：B．
【点睛】本题考查了完全平方公式的应用，掌握完全平方公式的结构特征是正确应用的前提．
10．（2021·重庆实验外国语学校九年级月考）如图1，某游池长25米，小林和小明两个人分别在游泳池的AB和CD两边，同时朝着另一边以各自的速度匀速游泳，他们游泳的时间为t（s），其中0≤t≤180，到AB边距离为y（m），图2中的实线和虚线分别表示小林和小明在游泳过程中y与t的对应关系，以下推断：①在整个游泳过程中，小林的总路程比小明的总路程更短；②小明游泳的速度是m/s；③两人第一次与第三次相遇的时间间隔是75s；④小林离AB边超过20米的总时长为36s．其中正确的个数是（ ）
A．1B．2C．3D．4
【答案】D
【分析】由图象可知，在整个游泳过程中，小明游了3个来回，小林游了2个来回，再根据“路程，速度与时间”的关系逐一判断即可．
【详解】解：①正确．在整个游泳过程中，小明游了3个来回，小林游了2个来回，故小林的总路程比小明的总路程更短；②正确．小明游泳的速度是：；③正确，
小林游泳的速度是：；两人第一次相遇时间为：，
两人第一次与第三次相遇的时间间隔是：，小明游75米时小林游了50米；④正确．
小林远离地超过20米的总时长为：；故选：．
【点睛】本题考查函数图象的应用，解题的关键是读懂图象信息，灵活运用所学知识解决问题，属于中考常考题型．
二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在横线上）
11．（2021·河北承德·八年级期末）琪琪拿9元钱去买单价为元/只的笔芯，买笔芯所剩的钱数（元）与所买笔芯的数量（只）之间的关系式为______．
【答案】
【分析】根据总价等于单价乘以数量可以算出购买笔芯用掉的钱，再根据剩余的钱数等于总钱数减去用掉的钱数，即可得出关系式．
【详解】解：由题知：买笔芯用去的钱数为：
所以买笔芯所剩的钱数为：故答案为：．
【点睛】本题主要考查列关系式，准确理解掌握“单价、数量和总价”以及“剩余钱数、用去的钱数与总钱数”之间的关系，是解决本题的关键．
12.（2021·安徽芜湖市·八年级期末）若，则____．
【答案】3
【分析】根据幂的乘方把算式中的各底数变成同底数，然后按同底数幂运算法则，列方程即可．
【详解】解： ， ，
，，，．故答案为：3
【点睛】本题考查了同底数幂的乘除和幂的乘方，根据题意，把底数变成相同是解题关键．
13．（2021·湖南长沙·八年级期末）如图，将大正方形通过剪、割、拼后分解成新的图形，利用等面积法可证明某些乘法公式，在给出的4幅拼法中，其中能够验证平方差公式的有 _________（填序号，多选）．
【答案】①②③
【分析】分别在两个图形中表示出阴影部分的面积，或者用两种方法表示同一个图形的面积，继而可得出验证公式．
【详解】解：在图①中，左边的图形阴影部分的面积＝a2﹣b2，右边图形中阴影部分的面积＝（a+b）（a﹣b），故可得：a2﹣b2＝（a+b）（a﹣b），可以验证平方差公式；
在图②中，除右下角阴影部分的面积外，剩余部分的面积可以表示为a2﹣b2，也可以表示为（a﹣b）（a+b），故可得：a2﹣b2＝（a+b）（a﹣b），可以验证平方差公式；
在图③中，左边的图形阴影部分的面积＝a2﹣b2，右边图形中阴影部分的面积＝（a+b）（a﹣b），故可得：a2﹣b2＝（a+b）（a﹣b），可以验证平方差公式；
在图④中，阴影部分的面积可以表示为（a+b）2﹣4ab，也可以表示为（a﹣b）2，由此可得（a+b）2﹣4ab＝（a﹣b）2，没法验证平方差公式．故答案为：①②③．
【点睛】本题主要考查了平方差公式，运用不同方法表示阴影部分面积是解题的关键．本题主要利用面积公式来证明a2﹣b2＝（a+b）（a﹣b）．
14．（2021·浦江县教育研究和教师培训中心七年级期末）若被除后余2，则的值为_____．
【答案】
【分析】先根据被除后余2，判断出为的一个因式，再根据特殊值法求得k的值．
【详解】被除后余2，可被整除，
为的一个因式，当 = 0时，= 0，
将代入= 0，得：，解得: k =-7，故答案为：-7．
【点睛】本题主要考查了整式的除法，理解被除式、除式、商、余式之间的关系是解题的关键．
15．（2021·广东佛山市七年级期中）如图，把一个长方形纸片沿EF折叠后，点D，C分别落在D′，C′的位置．若∠AED′=30°，则∠BFC′的度数为_________．
【答案】30°．
【解析】解：∵∠AED′=30°，∴∠DED′=180°-∠AED′=180°-30°=150°，
由折叠知：∠DEF=∠D′EF，∴∠DEF=∠DED′=×150°=75°．
∵AD∥BC，∴∠DEF=∠EFB=75°，∠DEF+∠EFC=180°，∴∠EFC=105°，
由折叠知：∠EFC=∠EF C′=105°，∴∠BFC′=∠EF C′-∠EFB=105°-75°30°. 故答案为30°．
16．（2021·湖北武汉·八年级期末）若a＝x＋20，b＝x＋19，c＝x＋21，则a2＋b2＋c2－ab－bc－ac＝______．
【答案】3
【分析】由已知a，b，c求出a−b，a−c以及b−c的值，原式乘以2变形，利用完全平方公式化简，将各自的值代入计算即可求出值．
【详解】解：∵a＝x＋20，b＝x＋19，c＝x＋21，∴a−b＝1，a−c＝−1，b−c＝−2，
原式＝（2a2＋2b2＋2c2−2ab−2bc−2ac）＝ [（a−b）2＋（b−c）2＋（a−c）2]＝3,故答案为：3．
【点睛】此题考查了因式分解的应用，熟练掌握完全平方公式是解本题的关键．
17．（2021秋•徐汇区校级期末）某空军加油飞机接到命令，立即给另一架正在飞行的运输机进行空中加油．在加油过程中，设运输飞机的油箱余油量为Q1吨，加油飞机的加油箱余油量为Q2吨，加油时间为t（分），Q1、Q2与t之间的函数图象如图所示，结合图象回答下列问题：
（1）加油之前，加油飞机的加油油箱中装载了 吨油；运输飞机的油箱有余油量 吨油；
（2）这些油全部加给运输飞机需 分钟；（3）运输飞机的飞行油耗为每分钟 吨油；
（4）运输飞机加完油后，以原速继续飞行，如果每分钟油耗相同，最多能飞行 小时．
【分析】（1）通过观察线段Q1，Q2段图象，不难得到加油飞机的加油油箱中装载了30吨油，运输飞机的油箱有余油量为40吨油．（2）将这些油全部加给运输飞机中需10分钟．
（3）首先根据运输飞机在10分钟时间内，加油29吨，但加油飞机消耗了30吨，求出每小时耗油量．
（4）根据（3）中的耗油量，可直接得出最多飞行时间．
【解析】（1）由题意及图象得
加油飞机的加油油箱中装载了30吨油，运输飞机的油箱有余油量为40吨油．故答案为：30；40．
（2）将这些油全部加给运输飞机中需10分钟；故答案为：10；
（3）∵运输飞机在10分钟时间内，加油29吨，但加油飞机消耗了30吨，
所以说10分钟内运输飞机耗油量为1吨，∴运输飞机每分钟耗油量为0.1吨；故答案为：0.1；
（4）由（3）知运输飞机每小时耗油量为＝6（吨），∴69÷6＝11.5（小时），故答案为：11.5．
18．（2021·湖北洪山·七年级期中）如图，已知AB∥CD，P为直线AB，CD外一点，BF平分∠ABP，DE平分∠CDP，BF的反向延长线交DE于点E，若∠FED＝a，试用a表示∠P为______．
【答案】∠P＝360°﹣2a
【分析】根据角平分线的性质得出∠1＝∠2，∠3＝∠4，平行线的性质得出∠1＝∠5，∠6＝∠PDC＝2∠3，进而根据三角形内角和得出∠5、∠FED，再得到∠P和a的关系，然后即可用 a表示∠P．
【详解】解：延长AB交PD于点G，延长FE交CD于点H，
∵BF平分∠ABP，DE平分∠CDP，∴∠1＝∠2，∠3＝∠4，
∵AB∥CD，∴∠1＝∠5，∠6＝∠PDC＝2∠3，
∵∠PBG＝180°﹣2∠1，∴∠PBG＝180°﹣2∠5，∴∠5＝90°﹣∠PBG，
∵∠FED＝180°﹣∠HED，∠5＝180°﹣∠EHD，∠EHD＋∠HED＋∠3＝180°，
∴180°﹣∠5＋180°﹣∠FED＋∠3＝180°，∴∠FED＝180°﹣∠5＋∠3，
∴∠FED＝180°﹣（90°﹣∠PBG）＋∠6＝90°＋（∠PBG＋∠6）＝90°＋（180°﹣∠P）＝180°﹣∠P，∵∠FED＝a，∴a＝180°﹣∠P∴∠P＝360°﹣2a．故答案为：∠P＝360°﹣2a．
【点睛】此题考查了角平分线的性质和平行线的性质及三角形内角和，有一定的综合性，认真找出角的关系是关键．
三、解答题（本大题共8小题，共66分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（2021·重庆实验外国语学校七年级期中）先化简，再求值：[（x+3y）2﹣（x﹣3y）2﹣（3y﹣x）（x+3y）﹣x2]÷（3y），其中x，y满足x2+4x+4+|y+1|＝0．
【答案】4x-3y；-5．
【分析】原式中括号中利用完全平方公式，平方差公式计算，去括号合并后利用多项式除以单项式法则计算得到最简结果，把与的值代入计算即可求出值．
【详解】解：原式＝（x2+6xy+9y2﹣x2+6xy﹣9y2+x2-9y2﹣x2）÷（3y）＝（12xy-9y2）÷（3y）＝4x-3y，
由x2+4x+4+|y+1|＝0，得到（x+2）2+ |y+1|＝0，解得：x＝-2，y＝﹣1，
则原式＝4×（-2）﹣3×（-1）＝﹣8+3=-5．
【点睛】此题考查了整式的混合运算化简求值，熟练掌握运算法则是解本题的关键．
20．（2021·江苏南京钟英中学）若（且，m、n是正整数），则．利用上面结论解决下面的问题：（1）如果，求x的值；（2）如果，求x的值；
（3）若，，用含x的代数式表示y．
【答案】（1）；（2）；（3）
【分析】（1）先,将底数都化为2，再利用同底数幂的乘除法法则计算；（2）利用积的乘方逆运算解答；
（3）利用等式的性质及幂的乘方逆运算将式子变形为，，即可得到x与y的关系式，由此得到答案．
【详解】解：（1）∵，∴，∴，解得；
（2）∵，∴，，，；
（3）∵，，∴，，
∴，∴．
【点睛】此题考查整式的乘法公式：同底数幂相乘、同底数幂相除、积的乘方以及幂的乘方的计算法则，熟记法则及其逆运算是解题的关键．
21．（2021·广西象州·七年级期中）阅读材料，解决问题．
材料一：比较和的大小．
解：因为，而，所以，即．
小结：在指数相同的情况下，可通过比较底数的大小，来确定两个幂的大小．
材料二：比较和的大小．
解：因为，而，所以，即．
小结：在底数相同的情况下，可以通过比较指数的大小，来确定两个幂的大小．
（1）比较，，的大小：（2）比较，，的大小．
【答案】（1）344＞433＞522；（2）8131＞2741＞961
【分析】（1）根据幂的乘方法则的逆运算进行变形，再比较大小；
（2）根据幂的乘方法则的逆运算进行变形，再比较大小．
【详解】解：（1）∵344=（34）11=8111，433=（43）11=6411，522=（52）11=2511，
∵81＞64＞25，∴8111＞6411＞2511，即344＞433＞522；
（2）∵8131=（34）31=3124，2741=（33）41=3123，961=（32）61=3122，
∵124＞123＞122，∴3124＞3123＞3122，即8131＞2741＞961．
【点睛】本题考查幂的乘方与积的乘方、有理数大小比较，解答本题的关键是明确有理数大小的比较方法．
22．（2021·福建省永春第一中学八年级月考）上数学课时，王老师在讲完乘法公式（a±b）2＝a2±2ab+b2的多种运用后，要求同学们运用所学知识解答：求代数式x2+4x+5的最小值？同学们经过交流、讨论，最后总结出如下解答方法：
解：x2+4x+5＝x2+4x+4+1＝（x+2）2+1
∵（x+2）2≥0，
∴当x＝﹣2时，（x+2）2的值最小，最小值是0，
∴（x+2）2+1≥1
∴当（x+2）2＝0时，（x+2）2+1的值最小，最小值是1，
∴x2+4x+5的最小值是1．
请你根据上述方法，解答下列各题
（1）知识再现：当x＝ 时，代数式x2﹣6x+12的最小值是 ；
（2）知识运用：若y＝﹣x2+2x﹣3，当x＝ 时，y有最 值（填“大”或“小”），这个值是 ；
（3）知识拓展：若﹣x2+3x+y+5＝0，求y+x的最小值．
【答案】（1）3，3；（2）1，大，−2；（3）y＋x的最小值为−6
【分析】（1）配方后即可确定最小值；（2）将函数解析式配方后即可确定当x取何值时能取到最小值；
（3）首先得到有关x＋y的函数关系式，然后配方确定最小值即可．
【详解】解：（1）∵x2−6x＋12＝（x−3）2＋3，∴当x＝3时，有最小值3；故答案为：3，3；
（2）∵y＝−x2＋2x−3＝−（x−1）2−2，∴当x＝1时有最大值−2；故答案为：1，大，−2；
（3）∵−x2＋3x＋y＋5＝0，∴x＋y＝x2−2x−5＝（x−1）2−6，
∵（x−1）2≥0，∴（x−1）2−6≥−6，∴当x＝1时，y＋x的最小值为−6．
【点睛】考查了因式分解的应用及非负数的性质，解题的关键是能够对二次三项式进行配方，难度不大．
23．（2021·无锡市天一实验学校七年级期中）（知识生成）通常情况下，用两种不同的方法计算同一图形的面积，可以得到一个恒等式．
（1）如图1，根据图中阴影部分（4个完全相同的小长方形）的面积可以得到的等式是： ．
（知识迁移）类似地，用两种不同的方法计算同一几何体的情况，也可以得到一个恒等式．如图2是边长为a+b的正方体，被如图所示的分割成8块．
（2）用不同的方法计算这个正方体的体积，就可以得到一个等式，这个等式可以为： ．
（3）已知a+b=3，ab=1，利用上面的规律求的值．
【答案】（1）（a+b）2-（a-b）2=4ab；（2）（a+b）3=a3+3a2b+3ab2+b3；（3）18
【分析】（1）∵阴影部分的面积=大正方形的面积-中间小正方形的面积 即：（a+b）2-（a-b）2，又∵阴影部分的面积由4个长为a，宽为b的小正方形构成 即：4ab即可求得；（2）大正方体被切割成了8个小正方体或长方体故而求它们的体积和，再直接求大正方体的体积可解的恒等式；（3）由（2）的结论将已知代入即可求得值．
【详解】解：（1）∵阴影部分的面积=大正方形的面积-中间小正方形的面积 即：（a+b）2-（a-b）2
又∵阴影部分的面积由4个长为a，宽为b的小正方形构成 即：4ab ∴（a+b）2-（a-b）2=4ab；
（2）∵八个小正方体或长方体的体积之和是：a3+a2b+a2b+ab2+a2b+ab2+ab2+b3
∴（a+b）3=a3+a2b+a2b+ab2+a2b+ab2+ab2+b3∴（a+b）3=a3+3a2b+3ab2+b3；
（3）∵由（2）可知（a+b）3=a3+3a2b+3ab2+b3∴a3+b3=（a+b）3-3a2b-3ab2=（a+b）3-3ab（a+b）
将a+b=3，ab=1代入上式可得a3+b3=33-3×1×3=18故a3+b3的值为：18．
【点睛】本题主要考查了平方差，立方和公式的几何背景，用分割求解和整体计算可解得．
24．（2021·河南驻马店市·七年级期末）已知：△ABC和平面内一点D．
（1）如图1，点D在BC边上，过D点作DE//BA交AC于点E，作DF//CA交AB于点F，判断∠EDF与∠A的数量关系，并说明理由．（2）如图2，点D在BC的延长线上，DF//CA，∠EDF＝∠A，请你判断DE与BA的位置关系．并说明理由． （3）如图3，点D在△ABC的外部，若作DE//BA，DF//CA，请直接写出∠EDF与∠A数量关系．
【答案】（1）相等，理由见解析；（2）平行，理由见解析；（3）相等或互补
【分析】（1）根据平行线的性质，即可得到∠A=∠EDF；
（2）延长BA交DF于G．根据平行线的性质以及判定进行推导即可；
（3）分两种情况讨论，即可得到∠EDF与∠A的数量关系：∠EDF=∠A，∠EDF+∠A=180°．
【详解】解：（1）∠EDF=∠A．理由：∵DE∥BA，DF∥CA，
∴∠A=∠DEC，∠DEC=∠EDF，∴∠A=∠EDF；
（2）DE∥BA．证明：如图，延长BA交DF于G．
∵DF∥CA，∴∠2=∠3．又∵∠1=∠2，∴∠1=∠3．∴DE∥BA．
（3）∠EDF=∠A，∠EDF+∠A=180°．理由：①如图，∵DE∥BA，DF∥CA，
∴∠D+∠E=180°，∠E+∠EAF=180°，∴∠EDF=∠EAF=∠BAC；
②如图，∵DE∥BA，DF∥CA，∴∠D+∠F=180°，∠F=∠CAB，∴∠EDF+∠BAC=180°．
综上，∠EDF与∠A相等或互补
【点睛】本题主要考查了平行线的性质以及判定的运用，解题时注意：平行线的判定是由角的数量关系判断两直线的位置关系；平行线的性质是由平行关系来寻找角的数量关系．
25．（2021·浙江温岭·八年级期末）公交公司员工小明住在站点的员工宿舍，每天早上去站点上班，站到站唯一一条公交线路示意图如图1，、、、是四个公交站点，其中、两站相距的路程是1200米，为了健身，小明往往沿公交线路步行到站或站后再乘公交车上班．
（1）星期一，小明步行到站上车，记他距站的路程为米，离开站的时间为分，关于的函数图象如图2，求的解析式及公交车的速度；
（2）星期二，小明以与星期一相同出发时间和步行速度步行到站上车，已知公交车无论上行（→）还是下行（→）都每隔10分钟一班，每天始发时间和行车速度保持不变，乘客上下车时间忽略不计；
①通过计算判断小明步行到达站时是否恰好有上行公交车到达站；
②小明到达站所用时间是星期一的1.5倍，求、两站相距的路程；
③若小明步行至站时刚好遇见一辆下行班车，这一趟上班途中，直接写出他遇到下行班车的最短间隔时间．
【答案】（1） 公交车的速度为：米分；（2）①小明步行到达站时恰好有上行公交车到达站；②、两站相距的路程是6600米；③分钟
【分析】（1）由图象上点可得小明步行的速度，从而可得函数解析式；由点的含义可得公交车的速度；
（2）①先计算小明步行到达站需要分，再计算上行公交车到达站需要分，而，从而可得小明步行到达站时恰好有上行公交车到达站；②设小明星期一所用时间为，星期二到达站所用时间为，可得，，再利用列方程，再解方程即可得到答案；③由每隔10分钟一班，每辆公交车相距米，而步行的速度小于坐车时的速度，可得最短时间间隔发生在坐车时，从而可得答案.
【详解】解：（1）由图象可知，小明步行的速度为（米分），
的解析式为，公交车的速度为（米分）；
（2）①小明步行到达站需要（分，
上行公交车到达站需要（分，
，小明步行到达站时恰好有上行公交车到达站；
②设小明星期一所用时间为，星期二到达站所用时间为，由题可知，，
小明到达站所用时间是星期一的1.5倍，，解得，
、两站相距的路程是6600米；
③每隔10分钟一班，每辆公交车相距（米，
步行的速度小于坐车时的速度，最短时间间隔发生在坐车时，间隔时间为（分钟）．
【点睛】本题考查的是从函数图象中获取信息，列函数关系式，一元一次方程的应用，理解题意与理解函数图象上点的坐标含义是解题的关键.
26．（2021·湖北十堰·七年级期末）已知ABCD，点E、F分别在AB、CD上，点G为平面内一点，连接EG、FG． （1）如图1，当点G在AB、CD之间时，请直接写出∠AEG、∠CFG与∠G之间的数量关系 ；（2）如图2，当点G在AB上方时，且∠EGF＝90°，求证：∠BEG –∠DFG＝90°；
（3）如图3，在（2）的条件下，过点E作直线HK交直线CD于K，使∠HEG与∠GEB互补，∠EKD的平分交与直线GE交于点L，请你判断FG与KL的位置关系，并证明．
【答案】（1）∠G＝∠AEG＋∠CFG；（2）90°；（3）FGKL，见解析
【分析】（1）过点G作，GH∥AB，则由平行线的性质可得∠AEG=∠EGH，∠CFG=∠FGH，即可推出∠EGF＝∠AEG＋∠CFG；（2）过点E作MN∥GF交CD于N，则∠GFN＝∠MND，∠G＝∠GEM＝90º，再由AB∥CD，得到∠MND＝∠MEB，即可得到∠BEG－∠DFG＝∠BEG－∠MEB＝∠GEM＝90º；
（3）先证明∠AEG＝∠HEG，从而得到∠BEL＝∠KEL＝∠BEK，再由角平分线的定义和平行线的性质即可得到∠ELK＝90º，从而可以利用同旁内角互补，两直线平行得证．
【详解】解：（1）∠EGF＝∠AEG＋∠CFG，理由如下：
如图所示，过点G作，GH∥AB，∵AB∥CD，∴AB∥CD∥GH，
∴∠AEG=∠EGH，∠CFG=∠FGH，∴∠AEG+∠CFG=∠EGH+∠FGH=∠EGF，∴∠EGF＝∠AEG＋∠CFG；
（2）过点E作MN∥GF交CD于N，则∠GFN＝∠MND，∠G＝∠GEM＝90º，
∵AB∥CD，∴∠MND＝∠MEB，∴∠BEG－∠DFG＝∠BEG－∠MEB＝∠GEM＝90º；
（3） FG∥KL．理由如下：
∵∠HEG＋∠GEB＝180º ，∠AEG＋∠GEB＝180º，∴∠AEG＝∠HEG，
∵∠BEL＝∠AEG，∠HEG＝∠KEL，∴∠BEL＝∠KEL＝∠BEK，
∵KL平分∠EKD，∴∠EKL＝∠EKD，∵AB∥CD，∴∠BEK＋∠EKD＝180º，
∴∠KEL＋∠EKL＝(∠BEK＋∠EKD)＝90º，∴∠ELK＝90º，
∵∠G＝90º，∴FG∥KL．
【点睛】本题主要考查了平行线的性质与判定，对顶角的性质，角平分线的定义，解题的关键在于能够熟练掌握相关知识进行求解．
放水时间(分钟)
1
2
3
4
…
游泳池中的水量(m3)
2480
2460
2440
2420
…