资料中包含下列文件,点击文件名可预览资料内容


















还剩8页未读,
继续阅读
成套系列资料,整套一键下载
第16章《二次根式》复习与小结 课件+过关测试(含答案解析) -人教版数学八年级下册
展开
这是一份第16章《二次根式》复习与小结 课件+过关测试(含答案解析) -人教版数学八年级下册,文件包含第十六章《二次根式》复习与小结课件-人教版数学八年级下册pptx、第十六章二次根式过关测试培优卷原卷版docx、第十六章二次根式过关测试基础卷原卷版docx、第十六章二次根式过关测试培优卷解析版docx、第十六章二次根式过关测试基础卷解析版docx等5份课件配套教学资源,其中PPT共16页, 欢迎下载使用。
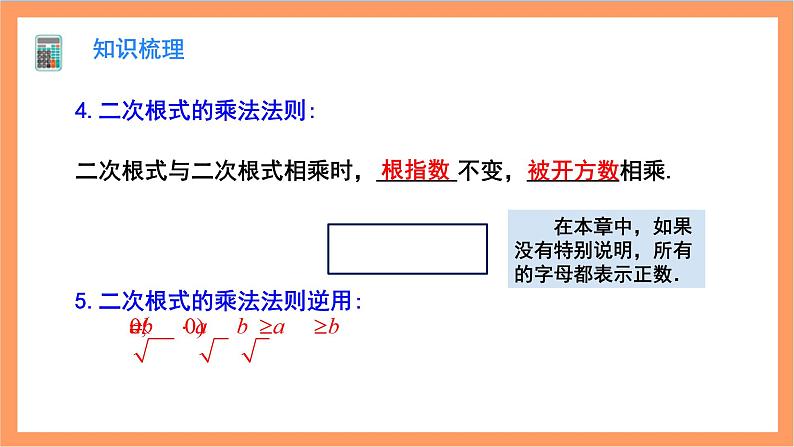
第16章《二次根式》复习与小结 人教版数学八年级下册知识梳理1.二次根式的概念:一般地,我们把形如 (a≥0)的式子叫做二次根式.2.如何确定二次根式中字母的取值范围?①被开方数不小于零;②分母中有字母时,要保证分母不为零.知识梳理3.二次根式的性质:a (a≥0)-a (a<0)知识梳理4.二次根式的乘法法则:根指数被开方数二次根式与二次根式相乘时, 不变, 相乘. 在本章中,如果没有特别说明,所有的字母都表示正数.5.二次根式的乘法法则逆用:知识梳理6.二次根式的除法法则:两个二次根式相除, 不变, 相除.根指数被开方数(a≥0,b>0) 二次根式的除法与乘法中b的取值范围不同,为什么?知识梳理7.二次根式除法法则的变形:8.最简二次根式:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.知识梳理化成最简二次根式后被开方数相同.9.同类二次根式: 一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.10.二次根式的加减法法则:步骤: “一化、二找、三合并”. 合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:知识梳理 1.二次根式混合运算顺序与实数中的运算顺序一样,先乘方,再乘除,最后算加减,有括号的先算括号里的(或者先去括号). 2.对于二次根式混合运算,实数中的运算律(分配律、结合律、交换律)运算法则及所有的乘法公式和分式的运算法则仍然适用. 3.二次根式的运算,可以类比整式的运算进行,在进行运算时,能用公式的尽量用公式.11.二次根式的混合运算:课堂练习1.二次根式 中,字母a的取值范围是 ( ) A. a> B. a< C. a≥ D. a≤D2.使 有意义的x的取值范围是 ( ) A.x≥3 B.x≥3且x≠4 C.x≤3 D.x<3B课堂练习3.下列式子中,属于最简二次根式的是 ( ) A. B. C. D. C4.如果最简二次根式 与 是同类二次根式,那么x的值是 ( ) A.-1 B. 0 C. 1 D. 2C课堂练习5.求使下列各式有意义的x的取值范围:解:-2≤x≤ .解:x≤0且x≠-1解:x≥0且x≠1.解:x≥ 且x≠2.6.计算:课堂练习课堂练习7.实数a,b满足 =0,求 的值. 解:由题意知,a2-6a+9=0,b-8=0, 即(a-3)2=0,b-8=0. 解得a=3,b=8. ∴课堂练习8.已知x=3 ,y=2 ,求下列各式的值:课堂练习课程结束人教版数学八年级下册
第16章《二次根式》复习与小结 人教版数学八年级下册知识梳理1.二次根式的概念:一般地,我们把形如 (a≥0)的式子叫做二次根式.2.如何确定二次根式中字母的取值范围?①被开方数不小于零;②分母中有字母时,要保证分母不为零.知识梳理3.二次根式的性质:a (a≥0)-a (a<0)知识梳理4.二次根式的乘法法则:根指数被开方数二次根式与二次根式相乘时, 不变, 相乘. 在本章中,如果没有特别说明,所有的字母都表示正数.5.二次根式的乘法法则逆用:知识梳理6.二次根式的除法法则:两个二次根式相除, 不变, 相除.根指数被开方数(a≥0,b>0) 二次根式的除法与乘法中b的取值范围不同,为什么?知识梳理7.二次根式除法法则的变形:8.最简二次根式:(1)被开方数不含分母;(2)被开方数中不含能开得尽方的因数或因式.知识梳理化成最简二次根式后被开方数相同.9.同类二次根式: 一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.10.二次根式的加减法法则:步骤: “一化、二找、三合并”. 合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:知识梳理 1.二次根式混合运算顺序与实数中的运算顺序一样,先乘方,再乘除,最后算加减,有括号的先算括号里的(或者先去括号). 2.对于二次根式混合运算,实数中的运算律(分配律、结合律、交换律)运算法则及所有的乘法公式和分式的运算法则仍然适用. 3.二次根式的运算,可以类比整式的运算进行,在进行运算时,能用公式的尽量用公式.11.二次根式的混合运算:课堂练习1.二次根式 中,字母a的取值范围是 ( ) A. a> B. a< C. a≥ D. a≤D2.使 有意义的x的取值范围是 ( ) A.x≥3 B.x≥3且x≠4 C.x≤3 D.x<3B课堂练习3.下列式子中,属于最简二次根式的是 ( ) A. B. C. D. C4.如果最简二次根式 与 是同类二次根式,那么x的值是 ( ) A.-1 B. 0 C. 1 D. 2C课堂练习5.求使下列各式有意义的x的取值范围:解:-2≤x≤ .解:x≤0且x≠-1解:x≥0且x≠1.解:x≥ 且x≠2.6.计算:课堂练习课堂练习7.实数a,b满足 =0,求 的值. 解:由题意知,a2-6a+9=0,b-8=0, 即(a-3)2=0,b-8=0. 解得a=3,b=8. ∴课堂练习8.已知x=3 ,y=2 ,求下列各式的值:课堂练习课程结束人教版数学八年级下册
相关资料
更多









