数学19.2.2 一次函数获奖ppt课件

这是一份数学19.2.2 一次函数获奖ppt课件，文件包含1922《一次函数》第3课时课件-人教版数学八年级下册pptx、1922一次函数重难点专项练习十大题型原卷版docx、1922一次函数重难点专项练习十大题型解析版docx等3份课件配套教学资源，其中PPT共21页， 欢迎下载使用。
1.理解待定系数法的意义.2.学会运用待定系数法和数形结合思想求一次函数解析式.
1.一般地，形如 的函数，叫做一次函数. 一次函数y=kx+b的性质：①当k>0时，y的值随着x值的 ；②当k2)
思考：你能由上面的函数解析式或函数图象解决以下问题吗？　（1）一次购买1.5kg种子，需付款多少元？（2）30元最多能购买多少种子？
解：（1）当x=1.5时，y=5x=7.5（元）； （2）在y=4x+2中，当y=30时，x=7.
1.一次函数y=kx+b(k≠0)的图象如图，则下列结论正确的是（ ） A．k=2　　　B．k=3　　　C．b=2　　D．b=3
2.如图，直线l是一次函数y=kx+b的图象，填空:　(1)b=______，k=______； (2)当x=30时，y=______； (3)当y=30时，x=______.
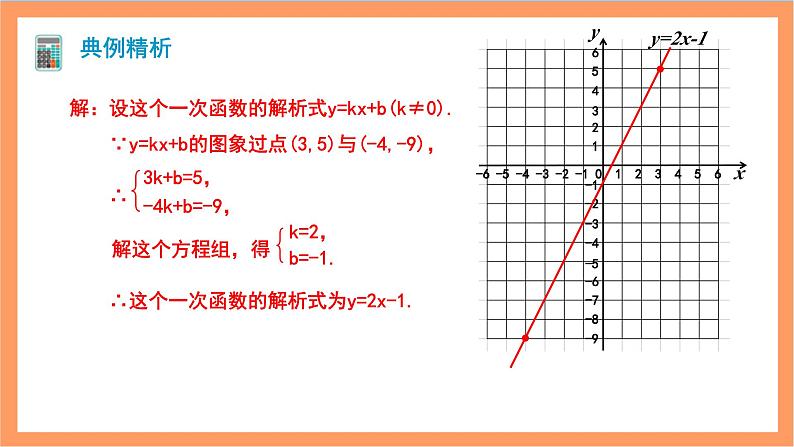
1.已知一次函数的图象过点（3，5）与（-3，-13），求这个一次函数的解析式．
解：设这个一次函数的解析式为y=kx+b.

解方程组得:
把点（3，5）与（-3，-13）分别代入，得：
2.正比例函数y=k1x与一次函数y=k2x+b的图象如图所示，它们的交点A的坐标为(3，4)，并且OB=5.(1)你能求出这两个函数的解析式吗？(2)△AOB的面积是多少呢？
解：（1）由题意可知，B点的坐标是（0，-5） ∵一次函数y=k2x+b的图象过点（0，-5），（3，4） ∴ ， 解得 ∴y=3x-5. ∵正比例函数y=k1x的图象过点（3，4）， ∴ ，即 .
（2）S△AOB=5×3÷2=7.5
1.若点A(-4，0)、B(0，5)、C(m，-5)在同一条直线上，则m的值是( ) A.8　 B.4 C.-6 D.-8 2.已知点P的横坐标与纵坐标之和为1，且这点在直线y=x+3上，则该点是( ) A.(-7，8) B.(-5，6) C.(-4，5) D.(-1，2)
3.若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行，求其解析式.
（1）设：设一次函数的一般形式 ；
（2）列：把图象上的点 ，代入一次函数的解析式，组成 方程组；
（3）解：解二元一次方程组得k,b；
（4）还原：把k,b的值代入一次函数的解析式.
求一次函数解析式的步骤：
y=kx+b(k≠0)
1.某品牌鞋子的长度y cm与鞋子的“码”数x之间满足一次函数关系．若22码鞋子的长度为16 cm，44码鞋子的长度为27 cm，求38码鞋子的长度？
2.某医药研究所开发了一种新药，在实际验药时发现，如果成人按规定剂量服用，那么每毫升血液中含药量y（毫克）随时间x（时）的变化情况如图所示，当成年人按规定剂量服药后.（1）服药后__时，血液中含药量最高，达到每毫升___毫克，接着逐步衰弱.（2）服药5时，血液中含药量为每毫升____毫克.（3）当x≤2时y与x之间的函数解析式是______.（4）当x≥2时y与x之间的函数解析式是________.（5）如果每毫升血液中含药量3毫克或3毫克以上时，治疗疾病最有效，那么这个有效时间是____时.