广西河池宜州区2023-2024学年九年级上学期期末考试数学试题

这是一份广西河池宜州区2023-2024学年九年级上学期期末考试数学试题，共9页。试卷主要包含了考试结束，上交答题卡等内容，欢迎下载使用。

注意：1．本试题卷满分120分，考试时间120分钟。
2．考生必须在答题卡上作答，在本试题卷上作答无效。
3．考试结束，上交答题卡。
一、选择题（每小题中只有一个选项符合要求，每小题3分，共36分。）
1．下列视力表的部分图案中，既是轴对称图形亦是中心对称图形的是（ ）
A．B．C．D．
2．下列事件是随机事件的是（ ）
A．瓮中捉鳖B．购买一张福利彩票，中奖
C．的绝对值等于2D．一个仅装着白球和黑球的袋中摸球，摸出红球
3．一元二次方程的根的情况是（ ）
A．没有实数根B．只有一个实数根
C．有两个相等的实数根D．有两个不相等的实数根
4．将二次函数的图象向左平移1个单位，再向下平移3个单位，所得函数图象的解析式是（ ）
A．B．
C．D．
5．假定鸟卵孵化后，雏鸟为雌鸟与雄鸟的概率相同．若3枚鸟卵全部成功孵化，则3只雏鸟中恰有2只雄鸟的概率是（ ）
A．B．C．D．
6．关于的方程是一元二次方程的条件是（ ）
A．且B．C．且D．
7．已知点在函数的图象上，则、、的大小关系为（ ）
A．B．C．D．
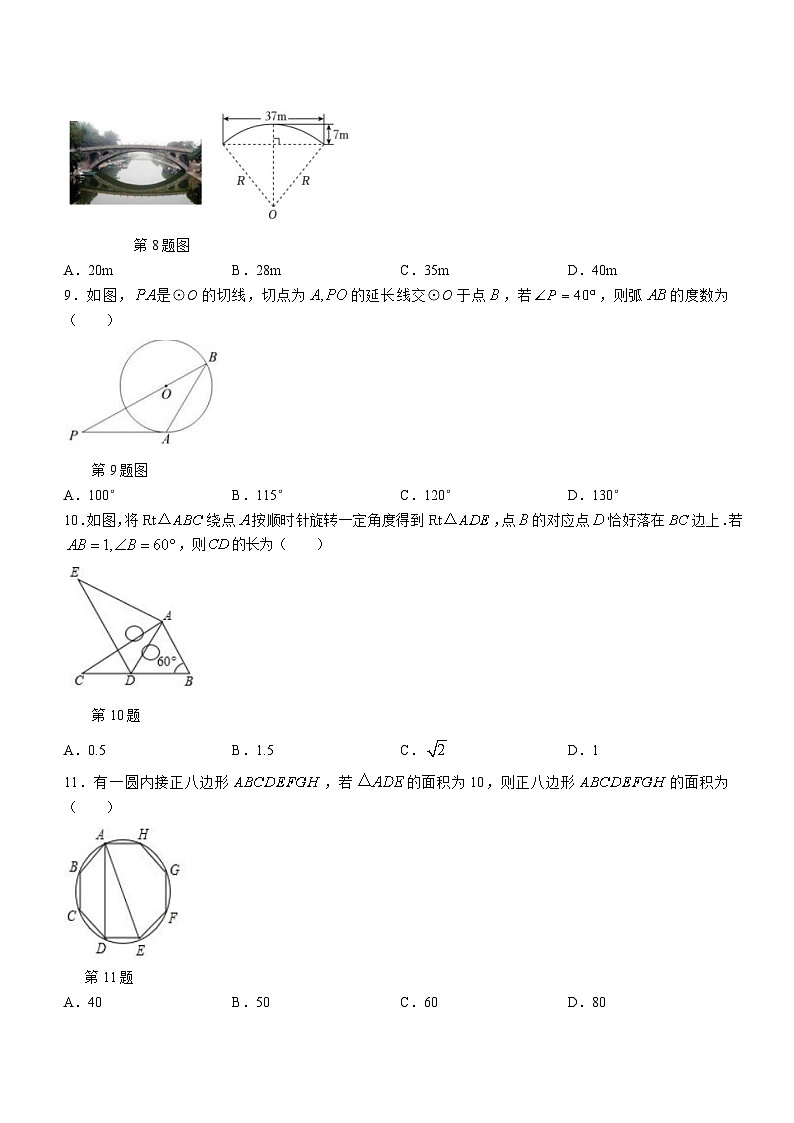
8．赵州桥是当今世界上建造最早，保存最完整的中国古代单孔敞肩石拱桥．如图，主桥拱呈圆弧形，跨度约为，拱高约为，则赵州桥主桥拱半径约为（ ）
第8题图
A．20mB．28mC．35mD．40m
9．如图，是⊙O的切线，切点为的延长线交⊙O于点，若，则弧的度数为（ ）
第9题图
A．100°B．115°C．120°D．130°
10．如图，将绕点按顺时针旋转一定角度得到，点的对应点恰好落在边上．若，则的长为（ ）
第10题
A．0.5B．1.5C．D．1
11．有一圆内接正八边形，若的面积为10，则正八边形的面积为（ ）
第11题
A．40B．50C．60D．80
12．对于二次函数当时的函数值总是非负数，则实数的取值范围为（ ）
A．B．C．D．或
二、填空题（本大题共6小题，每小题2分，共12分）
13．在平面直角坐标系中，点关于原点对称的点的坐标是______．
14．若关于的方程有一根为0，则______．
15．在二次函数中，函数与自变量的部分对应值如下表：
则______．
16．在一个不透明的口袋中装有4个红球和若干个白球，它们除颜色外其他完全相同，通过多次摸球试验后发现，摸到红球的频率稳定在25%附近，则口袋中白球可能有______个．
17．已知圆锥的高是12，底面圆的半径为5，则这个圆锥的侧面展开图的周长为______（结果保留）．
18．如图，是⊙O的一条弦，点是⊙O上一动点，且，点分别是的中点，直线与⊙O交于两点，若⊙O的半径为8，则的最大值为______．
第18题图
三、解答题：（本大题共8小题，共72分）
19．（6分）用合适的方法解下列方程
（1）（2）
20．（8分）如图，在平面直角坐标系中，的顶点坐标分别是，．
第20题图
（1）将平移得到，且的坐标是，画出；
（2）将绕点逆时针旋转90°得到，画出；
（3）小娟发现绕点旋转也可以得到，请直接写出点的坐标．
21．（8分）如图，在中，．
第21题图
（1）作的内切⊙O；分别与切于点（保留作图痕迹，不写作法）
（2）求（1）中⊙O的半径．
22．（10分）一个不透明的袋中装有2个红球、1个白球，这些球除颜色外，没有任何其他区别．有如下两个活动：
活动1：从袋中随机摸出一个球，记录颜色，然后从袋中剩余的球中再随机摸出一个球，摸出的两个球都是红球的概率记为；
活动2：从袋中随机摸出一个球，记录颜色，然后把这个球放回袋中并摇匀，重新从袋中随机摸出一个球，两次摸出的球都是红球的概率记为．
请你猜想，的大小关系，并用画树状图或列表的方法列出所有可能的结果，验证你的猜想．
23．（10分）解决问题：宜州区公安交警部门提醒市民，骑车出行必须严格遵守“一盔一带”的规定．某头盔经销商统计了某品牌头盔7月份到9月份的销量，该品牌头盔7月份销售500个，9月份销售720个，且从7月份到9月份销售量的月增长率相同．
（1）求该品牌头盔销售量的月增长率；
（2）若此种头盔的进价为30元/个，经市场预测，当售价为40元/个时，月销售量为600个，若在此基础上售价每上涨1元/个，则月销售量将减少10个，为使月销售利润达到10000元，而且尽可能让顾客得到实惠，该品牌头盔的实际售价应定为多少元？
24．（10分）如图，在中，，动点从点开始沿边向点以的速度移动（不与点重合），动点从点开始沿边向点以的速度移动（不与点重合）。如果两点分别从两点同时出发；
第24题图
（1）求出的面积随出发时间的函数解析式；
（2）求经过多少秒，四边形的面积最小？最小值是多少？
25．（10分）如图，在中，，点在上，以为半径的半圆交于点，交于点，点在上，且．
第25题图
（1）求证：是半圆的切线；
（2）若，求半圆的半径长．
26．（10分）如图，网格（每个小正方形的边长为1）中，有九个格点．
（1）抛物线的解析式为：．
①若经过点和，则______，______；
②若经过点和，该函数的解析式为：______；
（2）若抛物线经过这九个格点中的三个，求出所有满足这样的抛物线的解析式．
2023年秋期末考试九年级数学
参考答案
一、选择题（每小题3分，共36分）
二、填空题（每小题2分，共12分）
13． 14．0 15． 16．12 17． 18．12
三、解答
19．（1）解：
（2）解： ．
20．解：（1）如图
（2）如图
（3）
21．解：（1）作图略（画完整一个角平分线给一分）
第21题图
（2）连接
∵
∴四边形是矩形
∵ ∴四边形是正方形
设半径，则
根据切线长定理得：
∵，
即：解 得
22．解：猜想，理由如下：
活动1，画树状图如下：
共有6种等可能的结果，其中摸出的两个球都是红球的结果有2种，
；
活动2，画树状图如下：
共有9种等可能的结果，两次摸出的球都是红球的结果有4种，
，
∵，．
23．解：（1）设该品牌头盔销售量的月增长率为，
依题意，得：，
解得：（不合题意，舍去）．
答：该品牌头盔销售量的月增长率为．
（2）设该品牌头盔的实际售价为元，
依题意，得：，
整理，得：，
解得：（不合题意，舍去），，
答：该品牌头盔的实际售价应定为50元．
24．解：（1）由题意得：，，
（2）
∵ ∴当时，四边形面积最小，最小值是108
25．（1）证明（1）连接，如图1，
图1
∵，
∵，
∵，
，，是半圆的切线；
（2）连接，如图2，
图2
设圆的半径为，则，
∵，，
∵，，
．故圆的半径为．
26．（1）
（2）
【顶点是O，经过点和的解析式设是则把代入得：，则函数的解析式是：
【把向上平移一个单位长度即可得到顶点是，经过点和的解析式是：
【顶点是O，经过点和的解析式设是把代入得：，则函数的解析式是：
【顶点是且经过点和的解析式设是，把代入得：，则函数的解析式是：
【顶点是且经过点和的函数解析式设是把代入得则函数的解析式是：
【顶点是且经过点和的解析式是把代入得则函数的解析式是：
综上所述，满足这样的抛物线有6条（每对一个解析式给一分）0
1
2
3
4
7
2
2
7
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
B
A
A
C
C
A
B
D
D
A
A