数学八年级下册16.1 二次根式精品ppt课件

这是一份数学八年级下册16.1 二次根式精品ppt课件，文件包含1632《二次根式的混合运算》课件pptx、1632《二次根式的混合运算》教案docx、1632《二次根式的混合运算》分层作业原卷版docx、1632《二次根式的混合运算》分层作业解析版docx等4份课件配套教学资源，其中PPT共15页， 欢迎下载使用。

能根据运算律和相关法则进行二次根式的四则运算；
会说出二次根式四则运算的依据并用这些依据评估运算的正确性．
2.怎样合并同类根式？
几个二次根式化成最简二次根式后，如果被开方数相同，这几个二次根式就叫做同类二次根式.
（1）化为最简二次根式（2）系数相加减 （3）二次根式不变
3.二次根式的加减运算的步骤？
一化（最简二次根式）；二找（同类二次根式）；三合（同类二次根式）.
分析：把二次根式看成“项”,就可类比整式的运算进行.(1)、（2）类似于整式与整式乘法的“多项式乘以单项式”、“多项式除以单项式”.然后按照二次根式相应的运算法则进行.
　　思考：先计算什么？后计算什么，最后的目标是什么？
与有理数、实数运算一样，在混合运算中先乘除，后加减；对于（1）：先算乘，再化简，若有相同的二次根式进行合并，最后的目标是二次根式是最简二次根式；对于（2）：先算除，再化简，若有相同的二次根式进行合并，把所有的二次根式化成最简二次根式．
　　思考：每一步的依据是什么？　　　　　
第一步的依据是：分配律或多项式乘单项式；
　第二步的依据是：二次根式乘法法则；
第三步的依据是：二次根式化简．
　第二步的依据是：二次根式除法法则．
第一步的依据是：多项式除以单项式法则；
二次根式的加、减、乘、除混合运算与整式运算一样，体现在：运算律、运算顺序、乘法法则仍然适用.
平方差公式：（a+b)(a-b)=a2-b2;
分析：把二次根式看成“项”,就可类比整式的运算进行.类似于整式与整式乘法的“多项式乘以多项式”，然后按照二次根式相应的运算法则进行.
此处应用了(x+a)(x+b)=x2+(a+b)x+ab.
此处应用了（a+b)(a-b)=a2-b2.
教材14页练习1 计算：
教材14页练习2 计算：
化简已知条件和所求代数式
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2-(a+b)x+ab
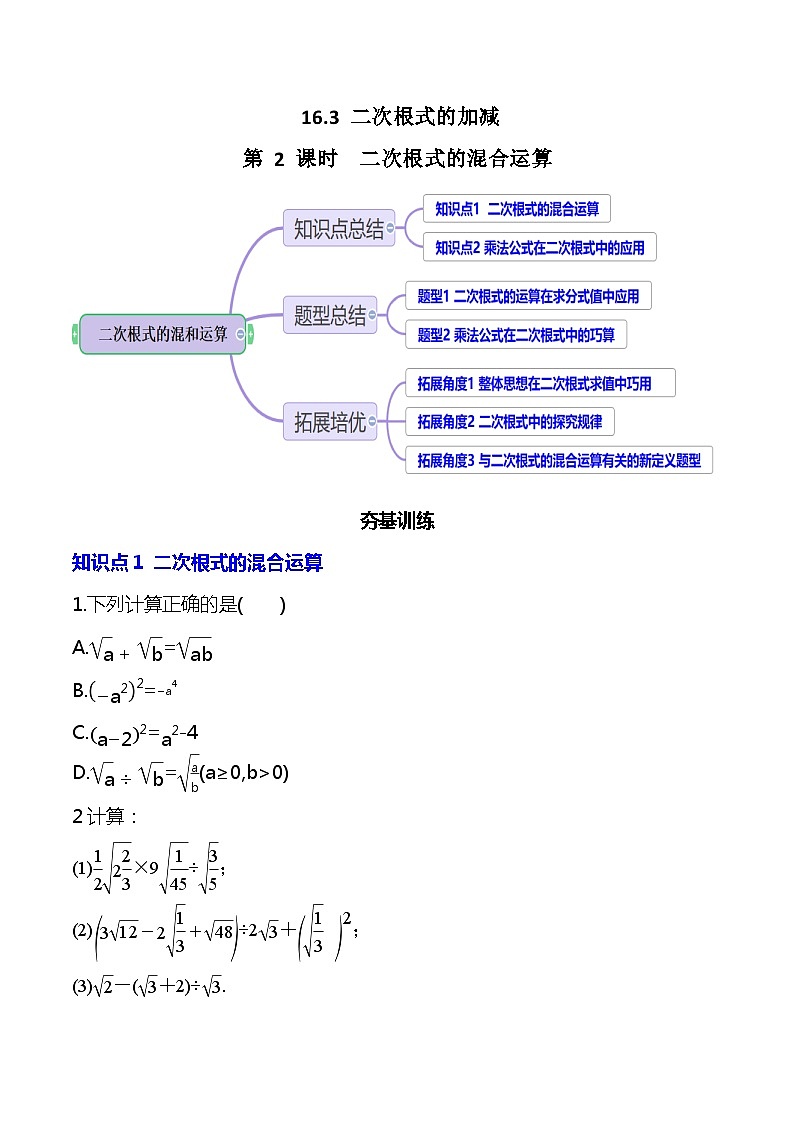
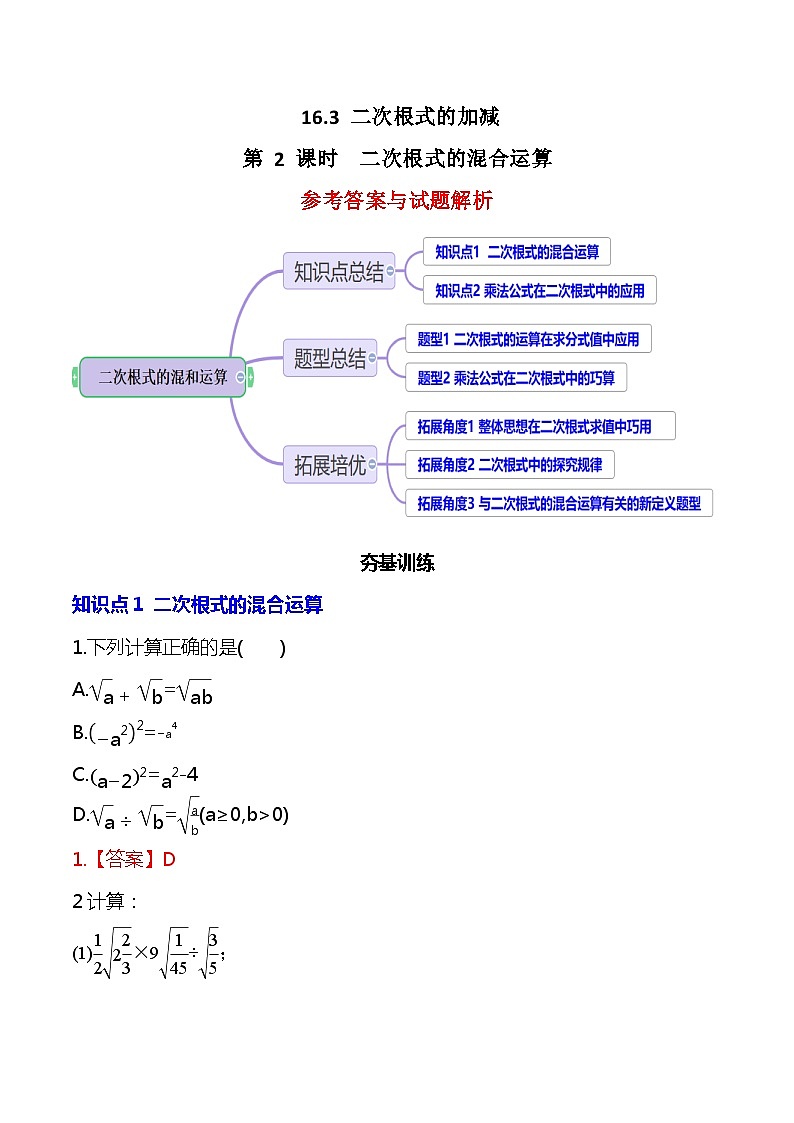
1.下列计算正确的是（ ）
A. 2 B. 4 C. 5 D.7
必做题：教科书第15页第4，6，7题；选做题：教科书第15页第8，9题