初中数学人教版八年级下册17.1 勾股定理精品课件ppt

这是一份初中数学人教版八年级下册17.1 勾股定理精品课件ppt，文件包含1711《勾股定理》课件pptx、1711《勾股定理》教案docx、1711《勾股定理》分层作业原卷版docx、1711《勾股定理》分层作业解析版docx等4份课件配套教学资源，其中PPT共19页， 欢迎下载使用。

了解勾股定理的发现过程，掌握勾股定理的内容，会用面积法证明勾股定理。
培养在实际生活中发现问题总结规律的意识和能力。
介绍我国古代在勾股定理研究方面所取得的成就，激发学生的爱国热情，促其勤奋学习。
相传2500年前，毕达哥拉斯有一次在朋友家里做客时，发现朋友家用砖铺成的地面中反映了A、B、C面积之间的数量关系进而发现直角三角形三边的某种数量关系．
数学家毕达哥拉斯的小故事
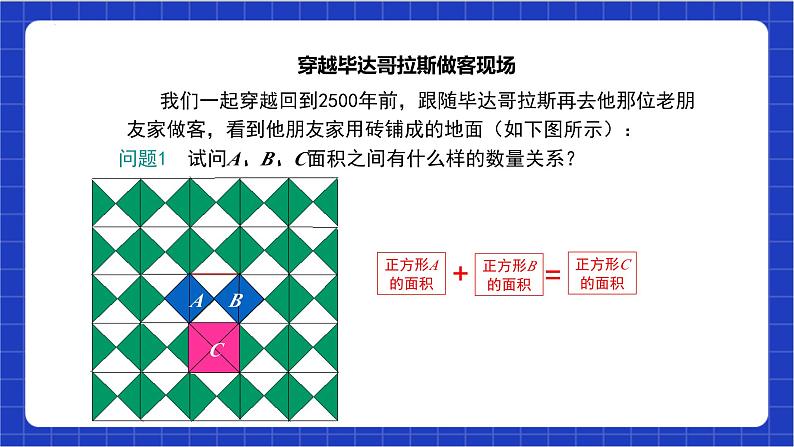
我们一起穿越回到2500年前，跟随毕达哥拉斯再去他那位老朋友家做客，看到他朋友家用砖铺成的地面（如下图所示）：
穿越毕达哥拉斯做客现场
问题1 试问A、B、C面积之间有什么样的数量关系？
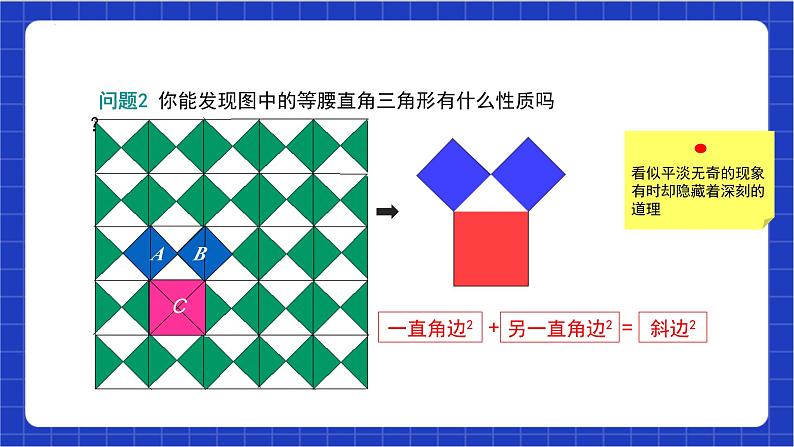
问题2 你能发现图中的等腰直角三角形有什么性质吗？
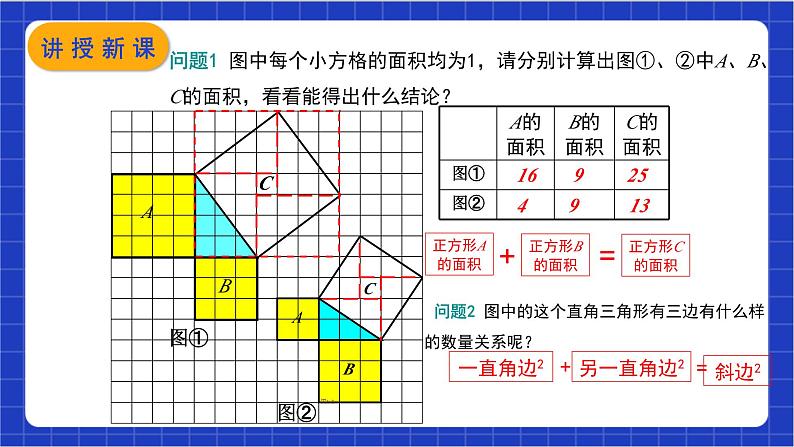
问题1 图中每个小方格的面积均为1，请分别计算出图①、②中A、B、C的面积，看看能得出什么结论？
问题2 图中的这个直角三角形有三边有什么样的数量关系呢？
命题1 如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
由上面的几个例子，我们猜想：
证明命题1的方法有很多，下面介绍我国古人赵爽的证法。 如图，这个图案是公元3世纪我国汉代的赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”．赵爽根据此图指出：四个全等的直角三角形（红色）可以如图围成一个大正方形，中间的部分是一个小正方形（黄色）．
这种用拼图的验证勾股定理的方法叫做弦图法
S小正方形＝（b-a）2
S大正方形＝4·S三角形＋S小正方形
这样我们就证实了命题1的正确性，命题1与直角三角形的边有关，我国把它称为勾股定理(Pythagras therem)“赵爽弦图”通过对图形的切割、拼接，巧妙地利用面积关系证明了勾股定理，它表现了我国古人对数学的钻研精神和聪明才智，是我国古代数学的骄傲。因此，这个图案被选为2002年在北京召开的国际数学家大会的会徽.
在我国又称商高定理，在外国则叫毕达哥拉斯定理，或百牛定理.
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
例1 如图，在Rt△ABC中， ∠C=90°.
（1）若a=b=5,求c;
（2）若a=1,c=2,求b.
1、设直角三角形的两条直角边长分别为a和b，斜边长为c.（1）已知a=6，c=10，求b；（2）已知a=5，b=12，求c； （3）已知c=25，b=15，求a.
解：由勾股定理得52+122=c2 , c=13;
解：由勾股定理得62+b2=102, b=8;
解：由勾股定理得a2+152=252 , a=20.
2.如图，图中所有的三角形都是直角三角形，四边形都是正方形，已知正方形A，B，C，D的边长分别是12，16，9，12，求最大正方形E的面积。
在Rt△ABC中， ∠C=90°,a,b为直角边，c为斜边，则有a2+b2=c2.
已知两边没有指明是直角边还是斜边时一定要分类讨论
1. 若一个直角三角形的两直角边长分别为9和12，则斜边的长为（ ） A.13 B.17 C. 15 D.18
2.若一个直角三角形的斜边长为17，一条直角边长为15，则另一直角边长为（ ） A.8 B.40 C.50 D.36
3.在Rt△ABC中，∠C=90°，若a︰b=3︰4，c=100，则a= _____，b = ______.
必做题：整理课堂中所提到的勾股定理的证明方法；选做题：通过上网等查找有关勾股定理的有关史料、趣事及其他证明方法