【核心素养】第17章《勾股定理》课件+教案+单元测试卷+专项训练卷（含答案解析）

这是一份【核心素养】人教版八年级下册数学第17章《勾股定理》课件+教案+单元测试卷+专项训练卷（含答案解析），文件包含第17章《勾股定理》小结与复习课件pptx、第17章《二次根式》小结与复习教案docx、第17章《勾股定理》专项训练卷原卷版docx、第17章《勾股定理》测试卷原卷版docx、第17章《勾股定理》测试卷解析版docx、第17章《勾股定理》专项训练卷解析版docx等6份课件配套教学资源，其中PPT共20页， 欢迎下载使用。

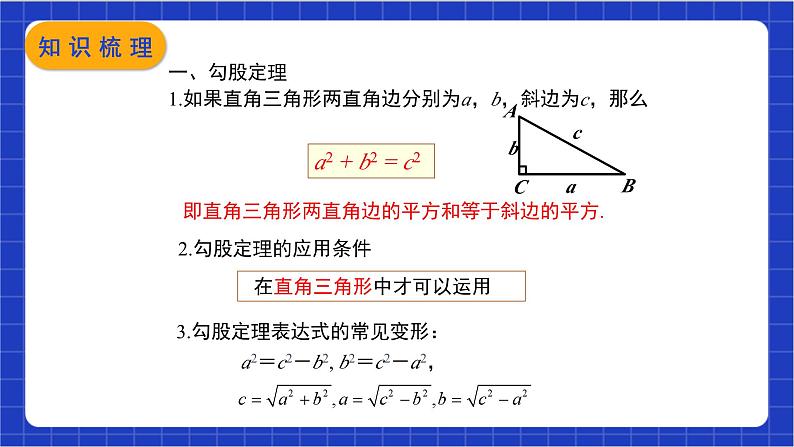
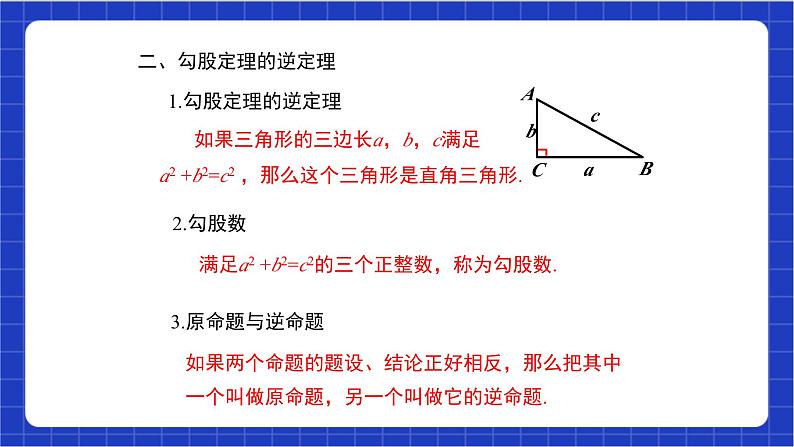
第17章《勾股定理》小结与复习人教版数学八年级下册回顾本章知识，在回顾过程中主动构建起本章知识结构；思考勾股定理及其逆定理的发现证明和应用过程， 体会出入相补思想、数形结合思想、转化思想在解决数学问题中的作用.素养目标 直角三角形是特殊的三角形，它的三边之间有特殊的数量关系.本章我们通过对面积关系的探究，发现并证明了勾股定理。勾股定理是数学中最重要的定理之一，它反映了直角三角形三边之间的数量关系，不仅在解决与直角三角形相关的问题时很有用，而且在解决其他许多数学问题时也很有用，借助于图形的面积研究相关的数量关系，是我国古代数学研究中经常采用的重要方法，它充分显示了古人的卓越智慧. 得到一个数学结论后，经常要研究其逆命题是否成立，一般地，原命题成立，逆命题未必成立，而勾股定理的逆命题是一个定理。勾股定理的逆定理提供了直角三角形的一种判定方法。勾股定理及其逆定理，从相反的路径对直角三角形进行了刻画.回顾思考1.直角三角形三边的长有什么特殊的关系?2.赵爽证明勾股定理运用了什么思想方法?3.已知一个三角形的三边长，怎样判断它是不是直角三角形?你作判断的依据是什么?4.证明勾股定理的逆定理运用了什么方法?5.一个命题成立，它的逆命题未必成立。请举例说明.请你带着下面的问题，复习一下全章的内容吧。1.如果直角三角形两直角边分别为a，b，斜边为c，那么a2 + b2 = c2即直角三角形两直角边的平方和等于斜边的平方. 在直角三角形中才可以运用2.勾股定理的应用条件一、勾股定理 3.勾股定理表达式的常见变形： a2＝c2－b2, b2＝c2－a2， 知识梳理二、勾股定理的逆定理1.勾股定理的逆定理 如果三角形的三边长a，b，c满足a2 +b2=c2 ，那么这个三角形是直角三角形. 满足a2 +b2=c2的三个正整数，称为勾股数.2.勾股数3.原命题与逆命题如果两个命题的题设、结论正好相反，那么把其中一个叫做原命题，另一个叫做它的逆命题.[题型一]：勾股定理的实际应用 10min后他们相距361m。 考题分类[题型一]：勾股定理的实际应用教材38页复习题17 3.如图，车床齿轮箱党要钻两个圆孔，两孔中心的距离是 134 m，两孔中心的水平距离是77mm.计算两孔中心的垂直距离(结果保留小数点后一位). 两孔中心的垂直距离约为109.7mm[题型一]：勾股定理的实际应用教材38页复习题17 4.如图，要修一个育苗棚，棚的横截面是直角三角形，棚宽a=3m，高b=1.5m,长d=10m求覆盖在顶上的塑料薄膜需多少平方米(结果保留小数点后一位).  [题型二]：勾股定理的直接应用   [题型三]：勾股定理的逆定理应用 是直角三角形。 (2)∠BCD是直角。[题型四]：互逆命题教材38页复习题176.下列各命题都成立，写出它们的逆命题。这些逆命题成立吗? (1)两条直线平行，同位角相等; (2)如果两个实数都是正数，那么它们的积是正数; (3)等边三角形是锐角三角形; (4)线段垂直平分线上的点到这条线段两个端点的距离相等 逆命题：同位角相等，两条直线平行;成立。逆命题：如果两个实数的积是正数，那么这两个实数都是正数;不成立。逆命题：锐角三角形是等边三角形;不成立。逆命题：到一条线段的两个端点距离相等的点在这条线段的垂直平分线上;成立。一、分类讨论思想 1.已知:直角三角形的三边长分别是3,4,X,则X2= 2.三角形ABC中,AB=10,AC=17,BC边上的高线AD=8,求BC25或71017817108 直角三角形中，已知两边长是直角边、斜边不知道时，应分类讨论。 当已知条件中没有给出图形时，应认真读句画图，避免遗漏另一种情况。思想方法二、方程思想直角三角形中，当无法已知两边求第三边时，应采用间接求法：灵活地寻找题中的等量关系，利用勾股定理列方程。如图，一块直角三角形的纸片，两直角边AC=6㎝，BC=8㎝。现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求CD的长． ACDBE第8题图Ｄx6x8-x46三、展开思想 几何体的表面路径最短的问题，一般展开表面成平面。 利用两点之间线段最短，及勾股定理求解如图是一个三级台阶，它的每一级的长宽和高分别为20dm、3dm、2dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是多少？２０２32323ＡＢＣ 如图，长方体的长为15 cm，宽为 10 cm，高为20 cm，点B离点C 5 cm,一只蚂蚁如果要沿着长方体的表面从点 A爬到点B，需要爬行的最短距离是多少？三、展开思想1020FEAECB2015105课堂小结必做题：教科书第39页复习题17第10，11题；选做题：教科书第39页复习题17第12，13，14题。课后作业课程结束人教版数学八年级下册