数学18.1.2 平行四边形的判定一等奖ppt课件

这是一份数学18.1.2 平行四边形的判定一等奖ppt课件，文件包含1812第1课时《平行四边形的判定1》课件pptx、1812第1课时《平行四边形的判定1》教案docx、1812第1课时《平行四边形的判定1》分层作业原卷版docx、1812第1课时《平行四边形的判定1》分层作业解析版docx等4份课件配套教学资源，其中PPT共21页， 欢迎下载使用。

在探索平行四边形的判别条件中，理解并掌握用边、对角线来判定平行四边形的方法．
会综合运用平行四边形的判定方法和性质来解决问题．
培养用类比、逆向联想及运动的思维方法来研究问题．
学习了平行四边形之后，小明回家用细木棒钉制了一个平行四边形.第二天，小明拿着自己动手做的平行四边形向同学们展示. 小辉却问：你凭什么确定这四边形就是平行四边形呢? 大家都困惑了……
两组对边分别平行的四边形叫平行四边形.
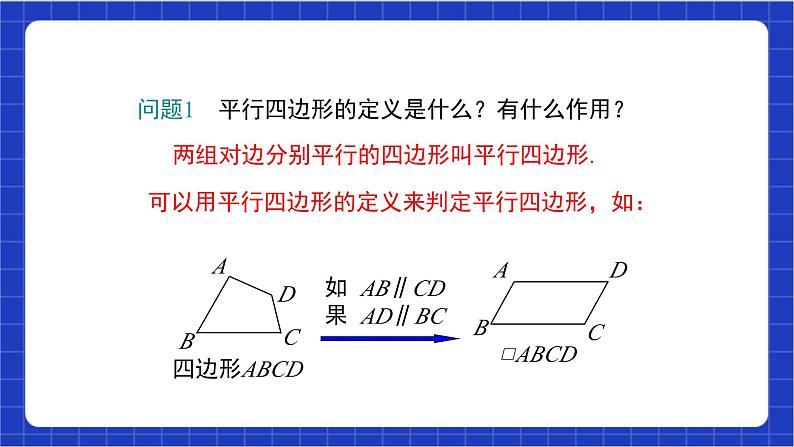
问题1 平行四边形的定义是什么？有什么作用？
可以用平行四边形的定义来判定平行四边形，如：
问题2 除了两组对边分别平行，平行四边形还有哪些性质？
平行四边形的对边相等.
平行四边形的对角相等.
平行四边形的对角线互相平分.
思考 我们得到的这些逆命题是否都成立？这节课我们一起探讨一下吧.
问题3 平行四边形上面的三条性质的逆命题各是什么？
两组对角分别相等的四边形是平行四边形；
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形；
你能根据平行四边形的定义证明它们吗？
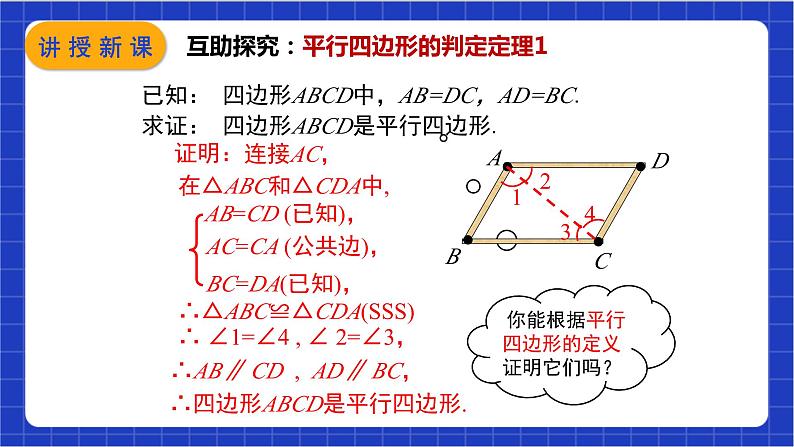
已知： 四边形ABCD中，AB=DC，AD=BC.求证： 四边形ABCD是平行四边形.
在△ABC和△CDA中,
AB=CD (已知)，
AC=CA (公共边)，
∴△ABC≌△CDA(SSS)
∴ ∠1=∠4 , ∠ 2=∠3，
∴AB∥ CD , AD∥ BC，
∴四边形ABCD是平行四边形.
互助探究：平行四边形的判定定理1
平行四边形的判定定理：两组对边分别相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵AB=CD,AD=BC,∴四边形ABCD是平行四边形.
例1 如图, AD⊥AC,BC⊥AC,且AB=CD,求证：四边形ABCD是平行四边形.
证明：在Rt△ABC和Rt△ACD中，∵AC=CA,AB=CD,∴Rt△ABC≌Rt△CDA(HL),∴BC=DA.又∵AB=CD,∴四边形ABCD是平行四边形．
教材47页练习1如图，AB=DC=EF,AD=BC,DE=CF.图中有哪些互相平行的线段？
解：∵AB=DC,AD=BC,∴四边形ABCD是平行四边形.∵DE=CF,DC=EF,∴四边形DCEF是平行四边形.∴AB//CD//EF,DE//C,AD//BC
已知：四边形ABCD中，∠A=∠C，∠B=∠D，求证：四边形ABCD是平行四边形.
又∵∠A=∠C，∠B=∠D，
∵∠A+∠C+∠B+∠D=360°，
∴2∠A+2∠B=360°，
即∠A+∠B=180°，
同理得 AB∥ CD，
互助探究：平行四边形的判定定理2
平行四边形的判定定理：两组对角分别相等的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵∠A=∠C，∠B=∠D,∴四边形ABCD是平行四边形.
例2 如图，四边形ABCD中，AB∥DC，∠B＝55°，∠1＝85°，∠2＝40°.(1)求∠D的度数；(2)求证：四边形ABCD是平行四边形．
(1)解：∵∠D＋∠2＋∠1＝180°，∴∠D＝180－∠2－∠1＝55°；(2)证明：∵AB∥DC，∴∠2＝∠CAB，∴∠DAB＝∠1＋∠2＝125°.∵∠DCB＋∠DAB＋∠D＋∠B＝360°，∴∠DCB＝∠DAB＝125°.又∵∠D＝∠B＝55°，∴四边形ABCD是平行四边形．
已知：四边形ABCD中，OA=OC，OB=OD.求证：四边 形ABCD是平行四边形.
在△AOB和△COD中,
OA=OC (已知)，
OB=OD (已知)，
∠AOB=∠COD (对顶角相等)，
∴△AOB≌△COD(SAS)，
∴ ∠BAO=∠OCD , ∠ABO=∠CDO,
∴AB∥ CD , AD∥ BC
互助探究：平行四边形的判定定理3
平行四边形的判定定理：对角线互相平分的四边形是平行四边形.
几何语言描述：在四边形ABCD中，∵AO=CO,DO=BO,∴四边形ABCD是平行四边形.
例3 如图， □ABCD 的对角线AC,BD相交于点O,E,F是AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形.
证明：∵四边形ABCD是平行四边形，
∴ AO=CO,BO=DO.
∴ AO-AE=CO-CF,即EO=OF.
∴四边形BFDE是平行四边形.
教材47页练习2如图， □ABCD 的对角线AC,BD相交于点O,E,F分别是OA，OC的中点。求证BE=DF.
平行四边形的判定（１）
①已知一组对边平行，可以证另一组对边平行，即定义法.
②已知一组对边相等，可以证另一组对边相等，构成判定定理1.
③已知一组对角相等，再证另一组对角相等，构成判定定理2.
④已知有一条对角线被平分，再证另一条对角线被平分，构成判定定理3.
1. 根据下列条件，不能判定一个四边形为平行四边形的是（ ）
A. 两组对边分别相等
B . 两条对角线互相平分
C . 两条对角线相等
D . 两组对边分别平行
2.能判定四边形ABCD是平行四边形的条件：∠A:∠B:∠C:∠D的值为（　　）
A. 1:2:3:4
B. 1:4:2:3
C. 1:2:2:1
D. 3:2:3:2
3. 如图所示，△ABC是等边三角形，P是其内任意一点，PD//AB,PE//BC,PF//AC,若△ABC的周长为24，则PD+PE+PF= .
必做题：教材第50页第5、6题； 选做题：教材第51页第13题．