人教版七年级下册5.3.1 平行线的性质精品教学ppt课件

这是一份人教版七年级下册5.3.1 平行线的性质精品教学ppt课件，文件包含人教版数学七年级下册531《平行线的性质》课件pptx、人教版数学七年级下册531《平行线的性质》教学设计docx、人教版数学七年级下册531《平行线的性质》导学案docx等3份课件配套教学资源，其中PPT共28页， 欢迎下载使用。
1. 掌握平行线的性质，会运用两条直线是平行关系判断角相等或互补；
2. 能够根据平行线的性质进行简单的推理.
根据右图，填空：①如果∠1＝∠C，　那么____∥____（ 　　　　　 　 ）② 如果∠1＝∠B 那么____∥____（ 　　 　　 　 ）③ 如果∠2＋∠B＝180°，　那么____∥____（ 　　 ）
同位角相等，两直线平行
内错角相等，两直线平行
同旁内角互补,两直线平行
问题：通过上题可知平行线的判定方法是什么？
思考：反过来,如果两条直线平行,同位角、内错角、同旁内角各有什么关系呢?
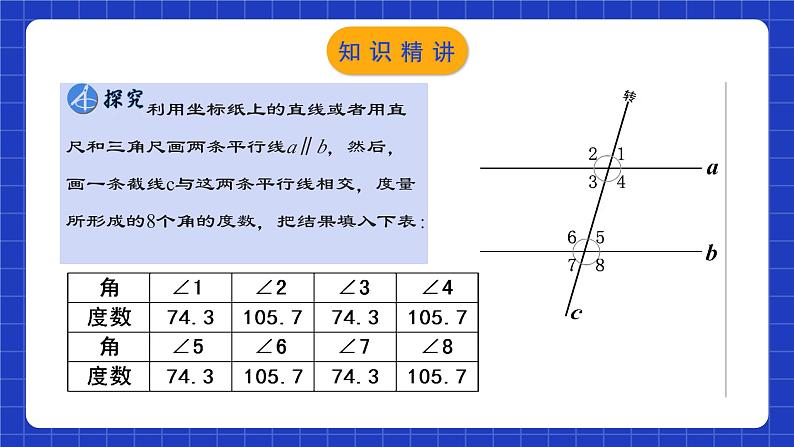
利用坐标纸上的直线或者用直尺和三角尺画两条平行线a∥b，然后，画一条截线c与这两条平行线相交，度量所形成的8个角的度数，把结果填入下表：
两条平行线被第三条直线所截，同位角______，内错角______，同旁内角______.
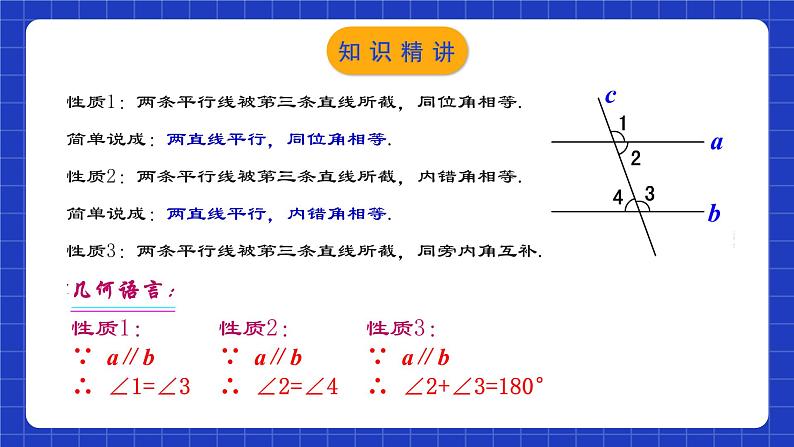
性质1：两条平行线被第三条直线所截，同位角相等.  简单说成：两直线平行，同位角相等.  性质2：两条平行线被第三条直线所截，内错角相等.  简单说成：两直线平行，内错角相等.  性质3：两条平行线被第三条直线所截，同旁内角互补.  简单说成：两直线平行，同旁内角互补.
在上一节中，我们利用“同位角相等，两直线平行线”推出了“内错角相等，两直线平行线”，类似地，已知两直线平行，同位角相等， 能否得到内错角之间的数量关系？
如图，你能根据性质1，说出性质2成立的道理吗？
∵ a∥b (已知)∴ ∠1=∠2 (_______________________)又∵ ∠1=____ (对顶角相等)∴ ∠2=∠3 (_________)
两直线平行，同位角相等
如图，你能根据性质1，说出性质3成立的道理吗？
∵ a∥b (已知)∴ ∠1=∠2 (两直线平行，同位角相等) 又∵ ∠1+∠3=180°(邻补角定义)∴ ∠2+∠3=180°(等量代换)
例1.如图是一块梯形铁片的残余部分，量得∠A=100°，∠B=115°，梯形的另外两个角分别是多少度？
解：如图，因为梯形上、下两底AB与CD互相平行，根据“两直线平行，同旁内角互补”，可得∠A与∠D互补，∠B与∠C互补. 于是 ∠D=180°-∠A=180°-100°=80° ∠C=180°-∠B=180°-115°=65° 所以梯形的另外两个角分别是80°、65°.
小明在纸上画了一个∠A，准备用量角器测量它的度数时，因不小心将纸片撕破，只剩下如图的一部分，如果不能延长DC、FE的话，你能帮他设计出多少种方法测出∠A的度数？
平行线三个性质的条件是什么？结论是什么？它与判定有什么区别？
例2.如图，直线AB//CD,∠EMB=100°,MF平分∠AME交CD于F,求∠EFM的大小.
解:∵∠EMB=100°，∠EMB+∠AME=180°，∴∠AME=80°.又∵MF平分∠AME，∴∠AMF=40°.又∵AB//CD，∴∠EFM=∠AMF=40°.
如图,直线AB//CD,∠1=65°，∠2=50°,试说明BC平分∠ABD.
解: ∵AB //CD ,∴∠ABC=∠1=65°,∠DBE=∠2=50°.∴∠CBD=180°-∠ABC-∠DBE=65°.∴∠ABC=∠CBD,即BC平分∠ABD.
例3.如图,AB // DE //GF,∠1:∠D:∠B=2:3:4,求∠1的度数.
解:∵∠1 :∠D:∠B=2:3:4,∴设∠1=2x°,∠D=3x°，∠B=4x°.∵AB//GF，∴∠GCB=(180-4x)°.∵DE//GF，∴∠FCD=(180-3x)°.∴∠1+∠GCB+∠FCD=180°，∴2x+180-4x+180-3x=180.解得x=36.∴∠1=72°.
例4.如图，EF//AD,EF//BC,CE平分∠BCF，∠DAC=120°.(1)求∠ACB的度数; (2)若∠ACF=20°,求∠FEC的度数.
解:(1)∵EF//AD,EF//BC，∴AD//BC.∴∠ACB+∠DAC=180°.∵∠DAC=120°，∴∠ACB=60°.
(2)∵∠ACF=20°，∴∠FCB=∠ACB-∠ACF=40°∵CE平分∠BCF，∴∠BCE=20°.∵EF//BC，∴∠FEC=∠ECB=20°.
如图,AB//CD,∠ABD的平分线与∠BDC的平分线交于点E,求∠1+∠2的度数.
1.如图，己知直线a，b被直线c所截，a//b， ∠1=60°则∠2的度数为( )A.30° B.60° C.120 D.150°2.如图，AB//CD,如果∠B=25°那么∠C为( )A.35° B.25° C. 55° D.65°
3.如图,已知直线a，b被直线c所截，以下结论正确的有( )①∠l=∠2; ②∠1=∠3; ③∠2=∠3; ④∠3+∠4=180°.A.1个 B.2个 C.3个 D.4个4.如图，AD//BC， 则一定有( )A.∠1=∠2 B.∠3=∠4 C.∠1=∠2,∠3=∠4 D.∠2=∠3
5.如图，下面推理不正确的是( )A.∵∠1=∠2 (已知)，∴CE//AB(内错角相等,两直线平行)B.∵∠2=∠4(已知)，∴DC//BF(同位角相等，两直线平行)C.∵BF//CD (已知)，∴∠3+∠4=180°(两直线平行，同旁内角互补)D.∵∠1=∠2， ∠2+∠3=180°(已知)∴∠1+∠3=180°，∴DC//BF(同旁内角互补，两直线平行)
6.如图(1)，AB//DE，∠BAF=115°，则∠ECF=______.7.如图(2)，直线a, b被直线c所截，若a//b，∠1=40°，∠2=70°，则∠3=_____.
8.如图(3)，已知AB// CD，直线EF分别交AB、CD于点E、F，EG平分∠BEF，若∠1=50°，则∠2=______.9.如图(4)，有一块含有60°角的直角三角板的两个顶点放在长方形的对边上，如果∠1=10°，则∠2=______.
10.如图(1)，已知AD，BC相交于点O.∵∠B=∠C (已知)∴_____//_____(内错角相等,两直线平行)∴∠A=_____(两直线平行，内错角相等)11.如图(2)，∵AB//EF (已知)∴∠A+________=180° (两直线平行，同旁内角互补)∵ED//CB (已知)∴∠DEF=________(两直线平行，内错角相等)
12.如图，AB//CD, AD//BC，问∠A与∠C有怎样的大小关系?为什么?
解:∠A=∠C, 理由如下:∵AD//BC (已知)∴∠A+∠B=180°(两直线平行， 同旁内角互补)又∵AB//CD (已知)∴∠C+∠B=180°(两直线平行,同旁内角互补)∴∠A=∠C (同角的补角相等)
13.如图，已知DE//BC，∠D:∠DBC=2:1，∠1=∠2，求∠DEB的度数.
解:∵DE//BC (已知)∴∠D+∠DBC=180°(两直线平行，同旁内角互补)∵∠D:∠DBC=2:1 (已知)∴∠DBC=60°(等式的性质)∵∠DBC=∠1+∠2且∠1=∠2 (已知)∴∠2=30°(等式的性质)∵DE//BC (已知)∴∠DEB=∠2=30°(两直线平行，内错角相等)