






数学第五章 相交线与平行线5.1 相交线5.1.1 相交线优质ppt课件
展开定义:如果两个角的和等于90°(直角),就说这两个角互为余角.
性质:同角(等角)的余角相等.
定义:如果两个角的和等于180°(平角),就说这两个角互为补角.
性质:同角(等角)的补角相等
1.理解邻补角与对顶角的有关概念,懂得邻补角与对顶角的区别与联系.
2.掌握邻补角与对顶角的性质,并能运用它们的性质进行角的计算及解决简单实际问题.
3.感知逻辑推理方法和过程.
观察剪刀剪东西的过程中有关角的变化.可以发现,握紧剪刀的把手时,随着两个把手之间的角逐渐变小,剪刀刃之间的角也相应变小.如果把剪刀的构造看作两条相交的直线,这就关系到两条相交直线所成的角的问题.
知识点1:邻补角与对顶角的概念
在剪刀剪东西的过程中,你能说说∠AOC 与∠AOD的位置保持怎样的关系吗?
∠AOC 和∠AOD有一条公共边OA,且∠AOC 的另一边是∠AOD 另一边的反向延长线.
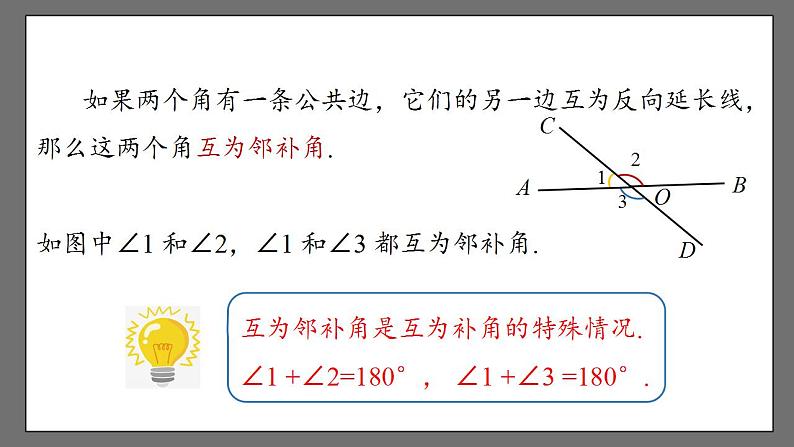
如果两个角有一条公共边,它们的另一边互为反向延长线,那么这两个角互为邻补角.如图中∠1 和∠2,∠1 和∠3 都互为邻补角.
互为邻补角是互为补角的特殊情况. ∠1 +∠2=180°, ∠1 +∠3 =180°.
注意:(1)邻补角是成对出现的,单独的一个角或两个以上的角不能称为邻补角.(2)邻补角不一定都是两条直线相交形成的,一条直线与射线(端点在直线上)相交,也可以得到一对邻补角.(3)互为邻补角的两个角一定互补,但互补的两个角不一定是邻补角.
1. [2022重庆荣昌区期末]下列各图中,∠1与∠2是邻补角的是 ( )
邻补角的识别方法互为邻补角的两个角必须满足以下条件:①有一条公共边;②另一条边互为反向延长线. 二者缺一不可.
剪刀剪东西的过程中,你能说说∠AOC 与∠BOD的位置保持怎样的关系吗?
∠AOC 和∠BOD 有公共顶点O,且∠AOC 的两边分别是∠BOD 两边的反向延长线.
如果两个角有一个公共顶点,并且其中一个角的两边是另一个角的两边的反向延长线,那么这两个角互为对顶角.如图中∠1 与∠3 互为对顶角,∠2 与∠4 互为对顶角.
注意:对顶角是成对出现的,指两个角之间的关系,一个角的对顶角只有一个..
2.下列各图中,∠1与∠2是对顶角的是( )
对顶角的识别方法两个角互为对顶角必须满足两个条件:①两个角有一个公共顶点;②一个角的两边分别是另一个角的两边的反向延长线.二者缺一不可.
知识点2: 邻补角与对顶角的性质
在上学期我们已经知道互为补角的两个角的和180°,因而互为邻补角的两个角的和为180°.
则有:∠1+∠2=180° ∠1+∠4=180° ∠2+∠3=180° ∠3+∠4=180°
问题:∠1 与∠3在数量上又有什么关系呢?
思考:你能利用有关知识来验证∠1 与∠3的数量关系吗?
已知:直线 AB 与 CD 相交于 O 点.求证:∠1=∠3.
证明:∵直线 AB 与 CD 相交于 O 点, ∴∠1+∠2=180°, ∠2+∠3=180°, ∴∠1=∠3. 同理可得∠2=∠4.
几何语言:∵直线 AB 与 CD 相交于 O 点, ∴∠1=∠3,∠2=∠4.
注意:两个角互为对顶角,它们一定相等,但相等的两个角不一定互为对顶角.
对顶角的性质:对顶角相等.
图中是对顶角量角器,你能说出用它测量角的度数的原理吗?
例1 如图,直线 a,b 相交,∠1=40°,求 ∠2,∠3,∠4 的度数.
解:由邻补角的定义,得 ∠2= 180°-∠1=180°-40°=140°. 由对顶角相等,得 ∠3=∠1=40°, ∠4=∠2=140°.
1. 【教材P35T2变式】如图,直线AB,CD相交所成的四个角中,∠1的邻补角为 ,若∠1∶∠2=1∶3,则∠1的度数为 .
2. 【2022苏州中考】如图,直线AB与CD相交于点O,∠AOC=75°,∠1=25°,则∠2的度数是 ( )A.25°B.30°C.40°D.50°
分析:∵∠AOC和∠BOD互为对顶角,∴∠AOC=∠BOD=75°,∴∠1+∠2=75°,∴∠2=75°-25°=50°.
3. 王麻子剪刀是北京市的传统工艺品,其锻制技艺被国务院列入第二批国家级非物质文化遗产名录,如图1是王麻子剪刀,把它抽象为图2所示,如果∠1+∠2=60°,那么∠3的度数是 ( )A.150°B.120°C.60°D.30°
分析: 根据对顶角的性质,可得∠1=∠2.∵∠1+∠2=60°,∴∠1=∠2=30°,∴∠3=180°-30°=150°.
4.(2021•益阳中考)如图,AB 与 CD 相交于点 O,OE 是 ∠AOC 的平分线,且 OC 恰好平分 ∠EOB,则∠AOD = 度.
分析: ∵OE 是 ∠AOC 的平分线,OC 平分 ∠EOB∴∠AOE=∠COE,∠COE=∠BOC∴∠AOE=∠COE=∠BOC=60°.∵∠AOD和∠BOC互为对顶角∴∠AOD=∠BOC=60°
5.如图,三条直线 l1 ,l2,l3 相交于一点,则∠1+∠2+∠3 等于( )A.90° B.120° C.180°D.360°
分析: ∵l1 ,l3 相交于一点,∴∠2=∠4,∵∠1+∠4+∠3=180°,∴∠1+∠2+∠3=180°.
6. 如图,直线AB,CD,EF相交于点O.(1)写出∠COE的邻补角;(2)分别写出∠COE和∠BOE的对顶角;(3)如果∠BOD=60°,∠BOF=90°,求∠AOF和∠FOC的度数.
6. 解:(1)∠COE的邻补角为∠COF和∠EOD.(2)∠COE和∠BOE的对顶角分别为∠DOF和∠AOF.(3)∵∠BOF=90°,∴∠AOF=180°-∠BOF=90°.∵∠BOD=60°,∴∠AOC=∠BOD=60°,∴∠FOC=∠AOF+∠AOC=90°+60°=150°.
1.如图,下列各组角中,互为对顶角的是( )A. ∠1和∠2 B. ∠1和∠3C. ∠2和∠4 D. ∠2和∠5
2.以下四个叙述中,正确的有( ) ①相等的角是对顶角;②互补的角是邻补角;③两条直线相交,可构成2对对顶角;④对顶角、邻补角都有一个共同特点:两个角有公共的顶点.A.4个 B.3个 C.2个 D.1个
3.如图所示:直线AB与CD相交于O,已知∠1=30°,OE是∠BOC的平分线,则∠2= °,∠3= °.
4.如图,直线AB,CD,EF相交于点O. (1)写出∠AOC, ∠BOE的邻补角; (2)写出∠DOA, ∠EOC的对顶角; (3)如果∠AOC =50°,求∠BOD ,∠COB的度数.
解:(1)∠AOC的邻补角是∠AOD和∠COB;∠BOE的邻补角是∠EOA和∠BOF.
(2)∠DOA的对顶角是∠COB;∠EOC的对顶角是∠DOF.
(3)∠BOD=∠AOC= 50°; ∠COB=180°-∠AOC=130°.
5.如图,两条直线 a,b 相交. (1) 如果 ∠1=50°,求 ∠2,∠3 的度数;
解:(1)∵∠1=50°,∠1+∠2=180°, ∴∠2=180°-50°=130°, 又∵∠3与∠1是对顶角, ∴∠3=∠1=50°.
(2) 如果 ∠2=3∠1,求 ∠3,∠4 的度数.
(2)∵∠2=3∠1,∠1+∠2=180°,∴∠1+3∠1=180°,∴4∠1=180°,∴∠1=45°,∴∠3=∠1=45°,又∵∠1+∠4=180°,∴∠4=180°-∠1=180°-45°=135°.
6.观察下列各图,寻找对顶角(不含平角) .
⑴ 如图a,图中共有 对对顶角;⑵ 如图b,图中共有 对对顶角;⑶ 如图c,图中共有 对对顶角;⑷ 研究⑴~⑶小题中直线条数与对顶角的对数之间的关系,猜测:若有n条直线相交于一点,则可形成 对对顶角;⑸ 若有10条直线相交于一点,则可形成 对对顶角.
人教版七年级下册第五章 相交线与平行线5.1 相交线5.1.1 相交线图片课件ppt: 这是一份人教版七年级下册第五章 相交线与平行线5.1 相交线5.1.1 相交线图片课件ppt,共10页。PPT课件主要包含了学习目标,重难点,情景导入,教学过程,探究新知,为什么呢,例题精讲等内容,欢迎下载使用。
初中人教版第五章 相交线与平行线5.1 相交线5.1.1 相交线课文配套课件ppt: 这是一份初中人教版第五章 相交线与平行线5.1 相交线5.1.1 相交线课文配套课件ppt,共14页。PPT课件主要包含了邻补角,对顶角,邻补角互补,对顶角相等,应用新知,练习小结,角的名称,位置关系,相同点,不同点等内容,欢迎下载使用。
初中数学人教版七年级下册5.1.1 相交线评课课件ppt: 这是一份初中数学人教版七年级下册5.1.1 相交线评课课件ppt,共17页。PPT课件主要包含了学习目标,课时讲解,课时流程,邻补角对顶角,知识点,邻补角,感悟新知,对顶角等内容,欢迎下载使用。













