浙江省温岭中学2021-2022学年高一下学期3月月考数学试卷(含答案)

这是一份浙江省温岭中学2021-2022学年高一下学期3月月考数学试卷(含答案)，共15页。试卷主要包含了选择题，多项选择题，填空题，解答题等内容，欢迎下载使用。

一、选择题
1．下列命题中真命题为( )
A.若且,则B.
C.D.为非零向量,若,则
2．在锐角中,已知,则的取值范围为( ).
A.B.C.D.
3．已知,,与夹角为,则在上的投影向量为( )
A.B.C.D.
4．在中,点D在边AB上,CD平分,若,,,,则等于( )
A.B.C.D.
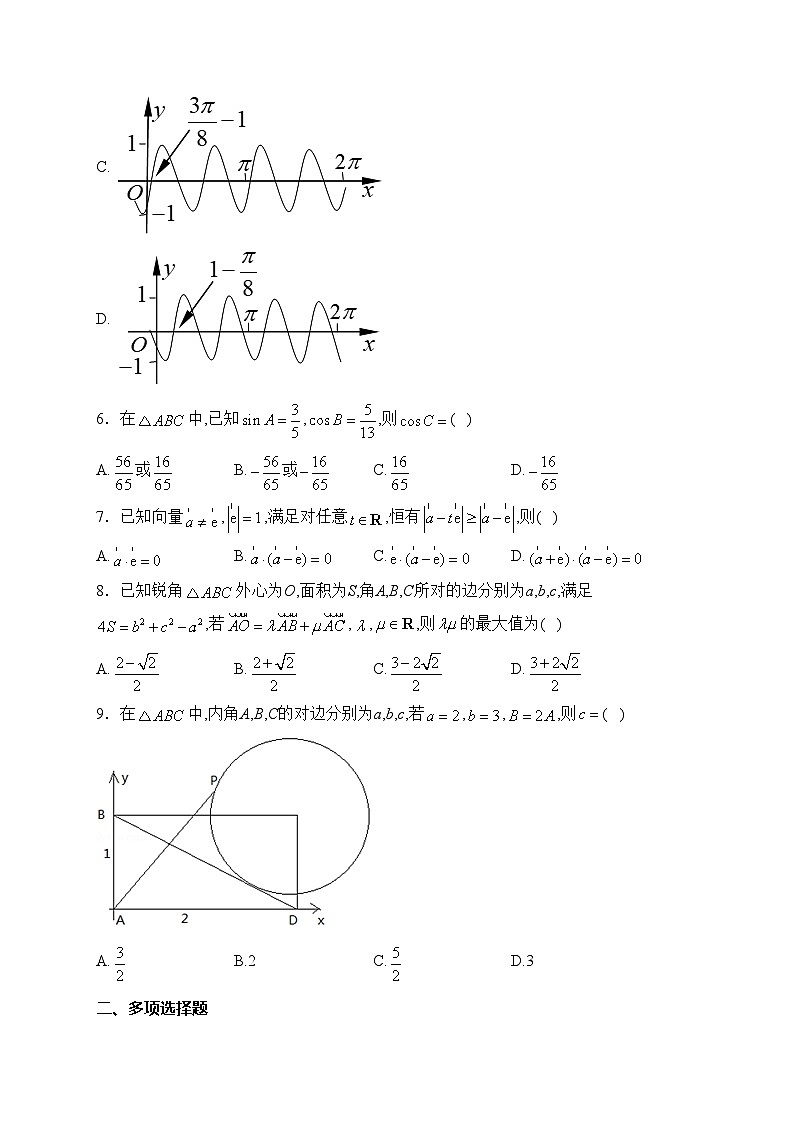
5．把函数的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下移1个单位长度,得到的图像为( ).
A.
B.
C.
D.
6．在中,已知,,则( )
A.或B.或C.D.
7．已知向量,,满足对任意,恒有,则( )
A.B.C.D.
8．已知锐角外心为O,面积为S,角A,B,C所对的边分别为a,b,c,满足,若,,,则的最大值为( )
A.B.C.D.
9．在中,内角A,B,C的对边分别为a,b,c,若,,,则( )
A.B.2C.D.3
二、多项选择题
10．已知O为坐标原点,点,,,,则( )
A.B.
C.D.
11．在矩形ABCD中,,,动点P在以点C为圆心且与BD相切的圆上.若,则可能的整数值为( )
A.3B.1C.0D.
12．设点P是边长为2的正方形ABCD内部及边界上的动点,则的取值可能为( )
A.B.2C.D.
三、填空题
13．若向量,满足,,,则_______.
14．在中,内角A,B,C的对边分别为a,b,c,且,若,则的面积是________.
15．在中,内角A,B,C的对边分别为a,b,c,若,且,则_________.
16．如图,中,,,AC的垂直平分线DE与AB,AC分别交于D,E两点,且,则__________.
四、解答题
17．已知两个向量,.
（1）求与垂直的单位向量;
（2）当实数k取何值时,向量与方向相反?
18．已知菱形ABCD的边长为1,,点E为边BC的中点,F为边CD上动点,
（1）求;
（2）当点F使得时,求的值.
19．在中,已知.
（1）求的值;
（2）若,M为AC中点,,求的值.
20．海岸上建有相距海里的雷达站C,D,某一时刻接到海上B船因动力故障发出的求救信号后,调配附近的A船紧急前往救援,雷达站测得角度数据为,,.
（1）救援出发时,A船距离雷达站C距离为多少?
（2）若A船以30海里每小时的速度前往B处,能否在3小时内赶到救援?
21．在锐角中,内角A,B,C的对边分别为a,b,c,面积为S,且满足.
（1）求B;
（2）求的取值范围.
22．在中,设,,若,,AD与BC交于点M,
（1）用,表示;
（2）在线段AC,BD上分别取E,F,使EF过M点,设,,求的最小值.
参考答案
1．答案：B
解析:对于选项A,若且,当时,则,当时,与关系无法确定,即选项A错误;
对于选项B,若,中至少有一个零向量,则命题显然成立,当,中都为非零向量时,若,则,则,,则,若,当或,显然,当或时,,若与不共线,则,即假设不成立,即,即选项B正确;
对于选项C,取,,不共线,则,,,即选项C错误;
对于选项D,,则,则或,即选项D错误;
故选:B.
2．答案：A
解析:在锐角三角形ABC中,,,
,,
又,
,
本题选择A选项.
3．答案：D
解析:在上的投影为,
在上的投影向量为.
故选:D.
4．答案：B
解析:因为CD平分,由角平分线定理得,
所以D为AB的三等分点,且,
所以,
故选:B.
5．答案：A
解析:
6．答案：C
解析:
7．答案：C
解析:
8．答案：C
解析:由,得,即,
因为A为三角形内角,所以,
因为锐角外心O在三角形内部,
,,,
设M,N分别为AB,AC的中点,
,
又,
所以①
同理,得②
①②联立得,
化简得,当且仅当时取等号,
解得或,
由①②得,,
所以,所以,即.
故选:C.
9．答案：C
解析:由正弦定理知,,
所以,所以,
由余弦定理知,,所以,化简得,,解得或2,当时,为等腰三角形,由,,知,即为等腰直角三角形,
所以,与题意不符,舍去,
综上,.
故选:C.
10．答案：ABD
解析:对A选项,,,
,故选项A正确;
对B选项,,
,故选项B正确;
对C选项,,,
,故选项C错误;
对D选项,,,
,故选项D正确.
故选:ABD.
11．答案：AB
解析:以A点为坐标原点,建立直角坐标系,
则,,
所以,,
圆C的半径为,
所以圆,
所以圆上点
所以,
因为,
所以,
所以,
所以,其中,,
所以,
所以,
即,
所以可能的整数值为:1,2,3,
故答案为:AB.
12．答案：BCD
解析:以A为坐标原点,AB所在直线为x轴,AD所在直线为y轴建立平面直角坐标系,
则,,,
设,则,,
则,,,
则
故当,时,取得最小值,
当或2,且时,取得最大值2,故的取值范围是
故选:BCD.
13．答案：
解析:,
所以,
解得,
所以.
故答案为:.
14．答案：24
解析:,,结合正弦定理得,
,即,
,B是三角形的内角
或,可得或,
,得a,b的长度不相等,
不成立,只有,可得,
因此,是直角三角形设,,可得,
,于是且,
由此可得的面积是,
故答案为:24
15．答案：
解析:由正弦定理及,知,
所以,
因为,所以,
因为,所以,
所以,
又,所以,
所以,
若,则,而,不存在此三角形;
若,则,即,
又,所以.
故答案为:.
16．答案：
解析:设,则,,.在中,,
在中,由正弦定理知,即,化简得,
所以,所以,,,.设,
在中,由余弦定理得,所以,所以,
在中,由余弦定理知,化简得.
17．答案：（1）见解析
（2）
解析:（1）,与之垂直的单位向量为或
（2）与不共线,当时,时同向舍去,
18．答案：（1）
（2）
解析:设,,
（1）原式
（2）设,则,,
又,,
19．答案：（1）
（2）或
解析:
（1）原式
（2）,设,
在中,,
当时,,
,
当时,,
,
或
20．答案：（1）120
（2）见解析
解析:（1）
（2）
,及时赶到.
21．答案：（1）见解析
（2）见解析
解析:（1）
（2）原式
锐角,且,,
,
原式
22．答案：（1）见解析
（2）见解析
解析:（1）设,
,M,D三点共线,,
,M,C三点共线,
联立解得:,
（2）,
,E,F三点共线,,
,
当即,时取到最小值.