





鲁教版 (五四制)六年级下册2 幂的乘方与积的乘方课堂教学课件ppt
展开会用数学的眼光观察现实世界:经历探索幂的乘方的运算法则的过程,进一步体会幂运算的意义。发展好奇心、想象力和创新意识。
会用数学的语言表示现实世界:经历用数学语言表示计算的过程,感悟数学与现实世界的交流方式,逐步养成用数学语言表达与交流的习惯。
会用数学的思维思考现实世界:理解幂的乘方法则的推理过程并会运用法则进行计算。培养讲道理、有条理的思维品质。
1.同底数幂的乘法法则:
6.2幂的乘方与积的乘方(第1课时:幂的乘方)
根据乘方的意义, 是 的3次方,表示 个 相乘,即 .
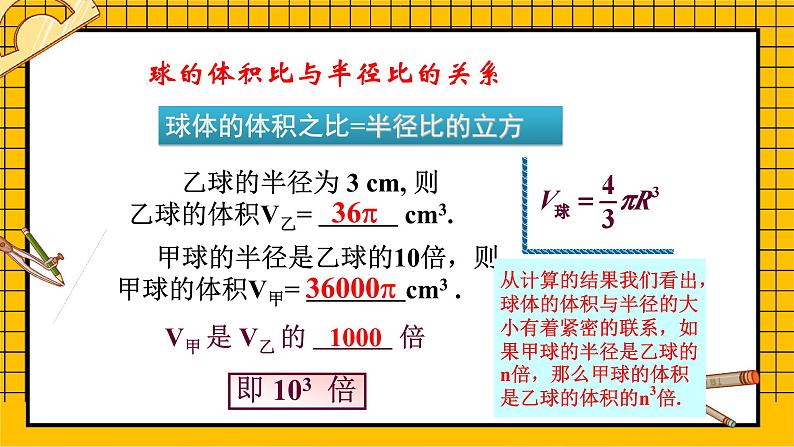
乙球的半径为 3 cm, 则乙球的体积V乙= cm3.
V甲 是 V乙 的 倍
即 103 倍
球的体积比与半径比的关系
甲球的半径是乙球的10倍,则甲球的体积V甲= cm3 .
从计算的结果我们看出,球体的体积与半径的大小有着紧密的联系,如果甲球的半径是乙球的n倍,那么甲球的体积是乙球的体积的n3倍.
球体的体积之比=半径比的立方
体积扩大的倍数比半径扩大的倍数大得多.
地球、木星、太阳可以近似地看作球体 。木星、太阳的半径分别约是地球的10倍和102倍,它们的体积分别约是地球的 倍和 倍.
=102×102×102
(根据 ).
(根据 ).
(102)3=106,为什么?
计算下列各式,并说明理由 .(1) (62)4 ; (2) (a2)3 ; (3) (am)2 ;
解:(1) (62)4
(2) (a2)3
= 62·62· 62·62
(am)n=amn (m,n都是正整数).
底数 ,指数 .
(同底数幂的乘法性质)
其中m , n都是正整数
想一想 (am)n 与 (an)m 相等吗?为什么?
请比较“同底数幂相乘的法则”与“幂的乘方法则”异同:
【例1】计算:(1) (102)3 ; (2) (b5)5 ; (3) (an)3; (4) -(x2)m ; (5) (y2)3 · y ; (6) 2(a2)6 - (a3)4 .
(6) 2(a2)6 - (a3)4
(1) (102)3
(5) (y2)3 · y
=2a2×6 - a3×4
1、计算:(1) (103)3 ; (2) -(a2)5 ; (3) (x3)4 · x2 ;(4) [(-x)2 ]3 ; (5) (-a)2(a2)2; (6) x·x4 – x2 · x3 .
2. 判断下面计算是否正确?如果有错误请改正:(1) (x3)3 = x6 ; (2)a6 · a4 = a24 .
1.计算:⑴ (x2)3· (x2)2 ⑵ (y3)4· (y4)3⑶ -(xn)2· (x3)2m
⑾ [(x+y)3]4
⑼ [(-1)3]5
⑿ [(a+1)3]n
解:255 = (25)11= 3211 344 = (34)11= 8111 433 = (43)11= 6411 522 = (52)11= 2511数值最大的一个是 344
5、在255,344,433,522这四个幂中,数值最大的一个是———。
公 式 的 反 向 使 用
(am)n=amn amn = (am)n
1、若 am = 2, 则a3m =_____.2、若 mx = 2, my = 3 , 则 mx+y =____, m3x+2y =______.
3、(1)已知2x+5y-3=0,求 4x · 32y的值 (2)已知 2x =a, 2y =b,求 22x+3y 的值 (3)已知 22n+1 + 4n =48, 求 n 的值 (5)比较375,2100的大小 (6)若(9n)2 = 38 ,则n为 .
2. 幂的乘方法则逆用:
习题6.2 第1、2题.
鲁教版五四制六年级下册数学
1、2×2 ×2=2( )
2、a·a·a·a·a = a( )
②乘方的结果叫做什么?
说出an的乘法意义,并将下列各式写成乘法形式:
=10×10×10×10×10×10×10×10
=(-2)×(-2)×(-2)×(-2)
(3) an = a × a × a ×… a n个a
3×105×3.15×107×4.22=39.879×(105×107)
105×107
=(10×10×10×10×10)×(10×10×10×10×10×10×10)
1、计算下列各式:(1)102×103(2)105×108(3)10m×10n(m,n都是正整数).
=(10×10)×(10×10×10)
=10×10×10×10×10
(根据 )
(根据 )
(根据 )
(根据 )
根据( )
根据( )
(根据 )
2. 2m×2n等于什么?
3. 和(-3)m×(-3)n呢?(m,n都是正整数)
猜想: am · an=? (当m、n都是正整数) 分组讨论,并尝试证明你的猜想是否正确。
am · an =
am · an = am+n (当m、n都是正整数)
am · an = am+n (当m、n都是正整数)
请你尝试用文字概括这个结论。
我们可以直接利用它进行计算.
幂的底数必须相同,相乘时指数才能相加.
(1)(-3)7×(-3)6 (2)
(3)-x3 · x5 (4)b2m· b2m+1
am · an · ap 等于什么?
方法1 am·an·ap
=(am·an)·ap
=am ·(an·ap )
方法2 am·an·ap
例2 光在真空中的速度约为3×105 km/s,太阳光照射到地球大约需要5×102s. 地球距离太阳大约有多远?
解:3×105×5×102 =15×107 =1.5×108(km)地球距离太阳大约有1.5×108 km.
(2) a7 ·a8
(3) x5 ·x3
(4) b5 · b
2. 计算:(1)x10 · x (2)10×102×104 (3)x5 ·x ·x3 (4)y4·y3·y2·y
(1)x10 ·x = x10+1= x11 (2)10×102×104 =101+2+4 =107(3)x5 ·x ·x3 = x5+1+3 = x9(4)y4 ·y3 ·y2 ·y= y4+3+2+1= y10
下面的计算对不对?如果不对,怎样改正?(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )(3)x5 ·x2 = x10 ( ) (4)y5 +2 y5 =3y10 ( )(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
m + m3 = m + m3
b5 · b5= b10
b5 + b5 = 2b5
x5 · x2 = x7
y5 + 2 y5 =3y5
c · c3 = c4
(1) x n · xn+1
(2) (x+y)3 · (x+y)4
x n · xn+1 =
(x+y)3 · (x+y)4 =
am · an = am+n
公式中的a可代表一个数、字母、式子等。
(x+y)3+4 =(x+y)7
2.填空:(1) 8 = 2x,则 x = ;(2) 8× 4 = 2x,则 x = ;(3) 3×27×9 = 3x,则 x = 。
3 .计算(-2)3×(-2)5 (2) (-2)2×(-2)7 (3) (-2)3×25 (4) (-2)2×27 (5)(x)2(-x)3(-x)(6)32×3×9 - 3×34
已知:am=2,an=3.求am+n =?
初中数学鲁教版 (五四制)六年级下册4 用尺规作角备课课件ppt: 这是一份初中数学鲁教版 (五四制)六年级下册<a href="/sx/tb_c26892_t3/?tag_id=26" target="_blank">4 用尺规作角备课课件ppt</a>,共19页。PPT课件主要包含了核心素养目标,圆规的功能是,复习回顾,情境导入,新知探究,交OA于点C,随堂练习,议一议,已知∠AOB,画图如图①②③④所示等内容,欢迎下载使用。
初中数学鲁教版 (五四制)六年级下册第五章 基本平面图形3 角评课ppt课件: 这是一份初中数学鲁教版 (五四制)六年级下册<a href="/sx/tb_c93702_t3/?tag_id=26" target="_blank">第五章 基本平面图形3 角评课ppt课件</a>,共22页。PPT课件主要包含了核心素养目标,旧知回顾,数学语言,新知探究,自学提示1,自学提示2,课堂练习,课堂小结,作业布置等内容,欢迎下载使用。
鲁教版 (五四制)六年级下册2 幂的乘方与积的乘方课前预习ppt课件: 这是一份鲁教版 (五四制)六年级下册<a href="/sx/tb_c26882_t3/?tag_id=26" target="_blank">2 幂的乘方与积的乘方课前预习ppt课件</a>,共21页。PPT课件主要包含了幂的乘方法则,旧知回顾,根据乘方的意义填空,探究新知,ab3,ab·ab·ab,a3·b3,anbn,幂的意义,abn等内容,欢迎下载使用。













