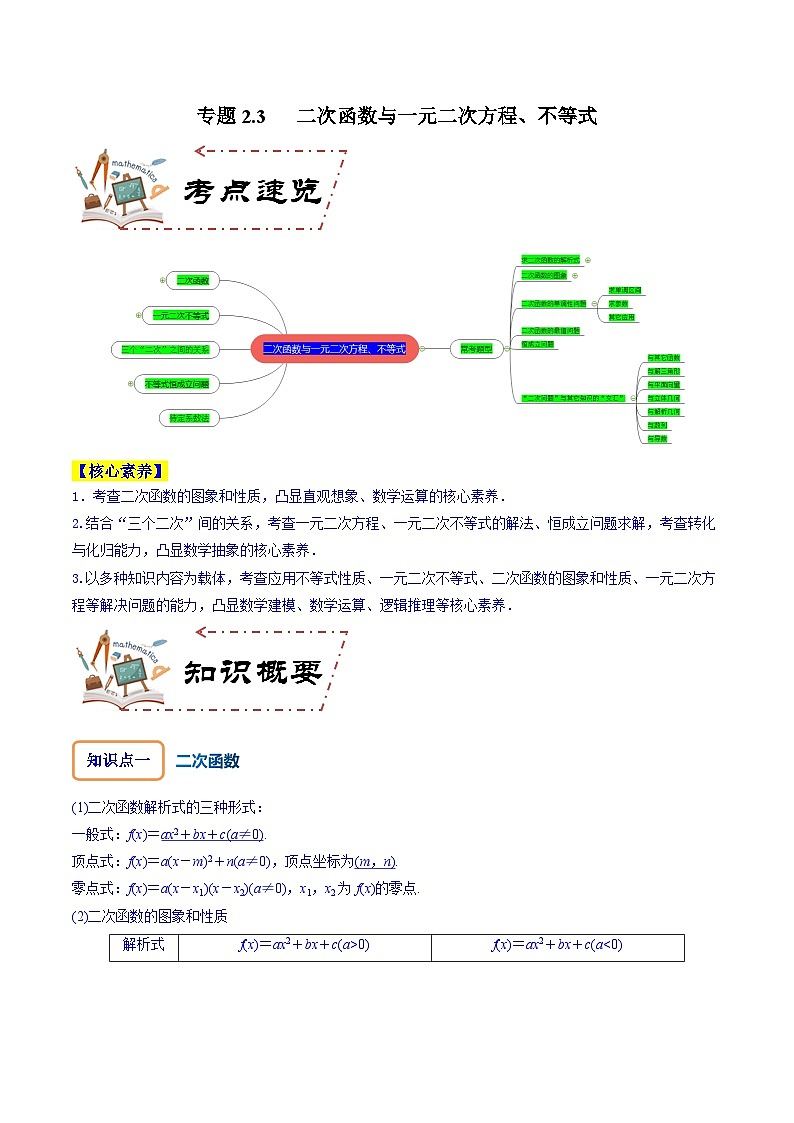

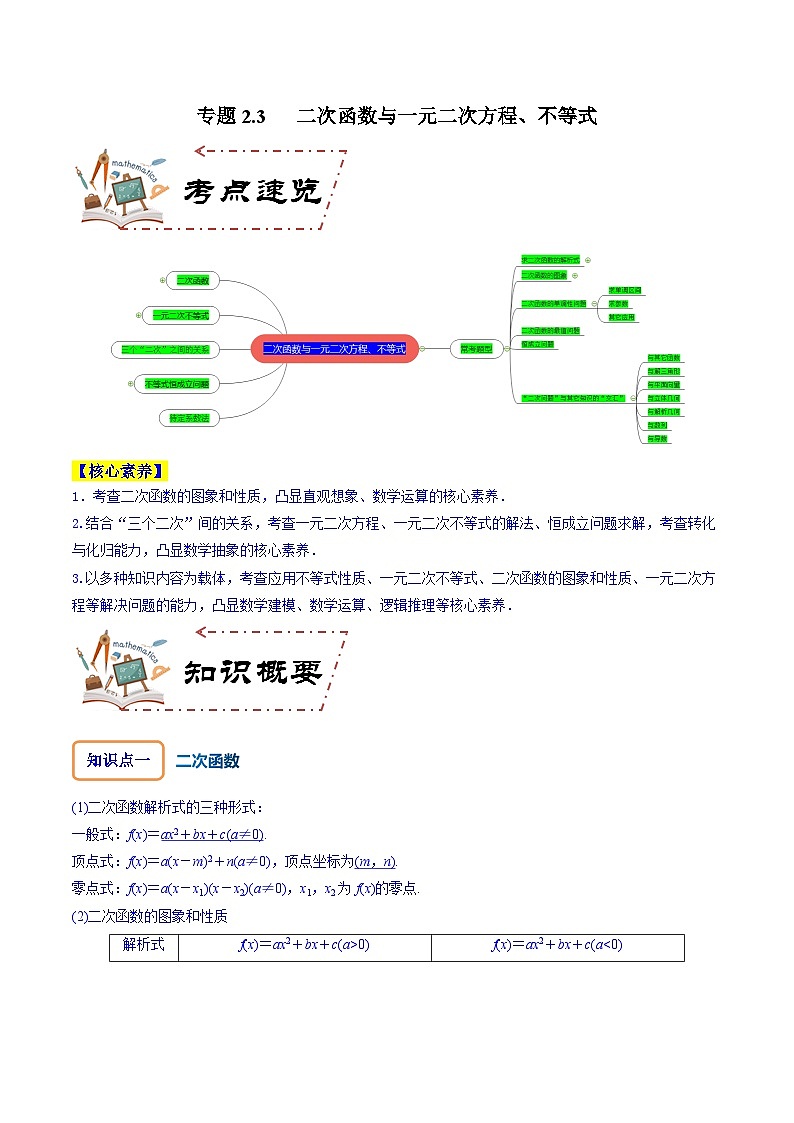

专题2.3 二次函数与一元二次方程、不等式-2024年高考数学大一轮复习核心考点精讲精练(新高考专用)
展开【核心素养】
1.考查二次函数的图象和性质,凸显直观想象、数学运算的核心素养.
2.结合“三个二次”间的关系,考查一元二次方程、一元二次不等式的解法、恒成立问题求解,考查转化与化归能力,凸显数学抽象的核心素养.
3.以多种知识内容为载体,考查应用不等式性质、一元二次不等式、二次函数的图象和性质、一元二次方程等解决问题的能力,凸显数学建模、数学运算、逻辑推理等核心素养.
知识点一
二次函数
(1)二次函数解析式的三种形式:
一般式:f(x)=ax2+bx+c(a≠0).
顶点式:f(x)=a(x-m)2+n(a≠0),顶点坐标为(m,n).
零点式:f(x)=a(x-x1)(x-x2)(a≠0),x1,x2为f(x)的零点.
(2)二次函数的图象和性质
知识点二
一元二次不等式
1.概念:我们把只含有一个未知数,并且知数的最高次数是2的不等式,称为一元二次不等式.
2.形式:
①ax2+bx+c>0(a≠0);
②ax2+bx+c≥0(a≠0);
③ax2+bx+c<0(a≠0);
④ax2+bx+c≤0(a≠0).
3.一元二次不等式的解集的概念:
一般地,使某个一元二次不等式成立的x的值叫做这个不等式的解,一元二次不等式的所有解组成的集合叫做这个一元二次不等式的解集.
知识点三
三个“二次”之间的关系
1.关于x的一元二次不等式ax2+bx+c>0(a≠0)或ax2+bx+c<0(a≠0)的解集;
若二次函数为f(x)=ax2+bx+c(a≠0),则一元二次不等式f(x)>0或f(x)<0的解集,就是分别使二次函数f(x)的函数值为正值或负值时自变量x的取值的集合.
2.三个“二次”之间的关系:
知识点四
不等式恒成立问题
1.一元二次不等式恒成立问题
(1)ax2+bx+c>0(a≠0)恒成立(或解集为R)时,满足eq \b\lc\{\rc\ (\a\vs4\al\c1(a>0,Δ<0));
(2)ax2+bx+c≥0(a≠0)恒成立(或解集为R)时,满足eq \b\lc\{\rc\ (\a\vs4\al\c1(a>0,Δ≤0));
(3)ax2+bx+c<0(a≠0)恒成立(或解集为R)时,满足eq \b\lc\{\rc\ (\a\vs4\al\c1(a<0,Δ<0));
(4)ax2+bx+c≤0(a≠0)恒成立(或解集为R)时,满足eq \b\lc\{\rc\ (\a\vs4\al\c1(a<0,Δ≤0)).
2.含参数的一元二次不等式恒成立.若能够分离参数成k
设f(x)的最大值为M,最小值为m.
(1)k
知识点五
待定系数法的应用
1.待定系数法解题的基本步骤是:
第一步,确定所求问题含有待定系数的解析式;
第二步,根据恒等的条件,列出一组含待定系数的方程;
第三步,解方程组或者消去待定系数,从而使问题得到解决.
2.如何列出一组含待定系数的方程,主要从以下几方面着手分析:
①利用对应系数相等列方程;
②由恒等的概念用数值代入法列方程;
③利用定义本身的属性列方程;
④利用几何条件列方程.
常考题型剖析
题型一:求二次函数的解析式
【典例分析】
例1-1.(2023·山东枣庄·统考模拟预测)已知二次函数,,且.
(1)求函数的解析式;
(2)求函数在区间上的值域.
【规律方法】
根据已知条件确定二次函数解析式,一般用待定系数法,选择规律如下:
【变式训练】
变式1-1. 已知二次函数f(x)满足f(2)=-1,f(-1)=-1,且f(x)的最大值是8,试确定该二次函数的解析式.
题型二:二次函数的图象
例2-1.(2022秋·安徽合肥·高一中国科技大学附属中学校考阶段练习)已知函数的部分图象如图所示,则( )
A.B.6C.D.3
例2-2.(2022秋·广西柳州·高一柳铁一中校联考阶段练习)已知函数的图像如图所示,则的图像可能是( )
A.B.
C.D.
例2-3.(2023·北京·高三专题练习)已知二次函数,对任意的,有,则的图象可能是( )
A.B.
C.D.
【规律方法】
识别二次函数图象应学会“三看”
【变式训练】
变式2-1.(2021秋·高一课时练习)已知函数(其中)的图象如图所示,则函数的图象是( )
A.B.
C.D.
变式2-2. (2023春·上海杨浦·高二上海市控江中学校考阶段练习)设均为非零实数,则直线和在同一坐标系下的图形可能是( ).
A.B.
C.D.
变式2-3. 【多选题】(2022秋·江西·高一统考阶段练习)设,则函数的图象可能是( )
A.B.
C.D.
题型三:二次函数的单调性问题
【典例分析】
例3-1.(2022秋·广东肇庆·高一德庆县香山中学校考开学考试)已知二次函数在区间内是单调函数,则实数的取值范围是( )
A.或B.
C.或D.
例3-2.(2023春·贵州黔东南·高一校考阶段练习)已知二次函数对任意的x都有,且的图象与x轴的两个交点间的距离为6.
(1)求的解析式;
(2)设,若在上是减函数,求的最小值.
【规律方法】
1.主要有三类问题:确定函数的单调区间、根据单调性求参数和应用单调性解题(如解不等式或求最值);
2. 研究二次函数单调性的思路
(1)二次函数的单调性在其图象对称轴的两侧不同,因此研究二次函数的单调性时要依据其图象的对称轴进行分类讨论.
(2)若已知f(x)=ax2+bx+c(a>0)在区间A上单调递减(单调递增),则A⊆eq \b\lc\(\rc\](\a\vs4\al\c1(-∞,-\f(b,2a)))eq \b\lc\(\rc\)(\a\vs4\al\c1(A⊆\b\lc\[\rc\)(\a\vs4\al\c1(-\f(b,2a),+∞)))),即区间A一定在函数对称轴的左侧(右侧).
【变式训练】
变式3-1.(2021·浙江高三专题练习)若函数在内不单调,则实数a的取值范围是__________.
变式3-2.(2022秋·高一单元测试)已知函数与在区间上都是减函数,那么__________.
题型四:二次函数的最值问题
【典例分析】
例4-1. (2023·四川·四川省金堂中学校校联考三模)已知函数是定义在上的奇函数,且当时,,则的最小值是( )
A.B.C.1D.2
例4-2.(2023·全国·高三专题练习)函数在区间上的最大值为.求的解析式;
【规律方法】
二次函数最值问题的类型及求解策略
(1)类型:①对称轴、区间都是给定的;②对称轴动、区间固定;③对称轴定、区间变动.
(2)解决这类问题的思路:抓住“三点一轴”数形结合,三点是指区间两个端点和中点,一轴指的是对称轴,结合配方法,根据函数的单调性及分类讨论的思想即可完成.
【变式训练】
变式4-1.(2021·长春市第二实验中学高二月考(文))函数在上的最大值和最小值依次是( )
A.,B.,C.,D.,
变式4-2.(2023·重庆·统考二模)已知,,则的最小值为___________.
题型五:恒成立问题
【典例分析】
例5-1.(江西高考真题)若不等式对于一切恒成立,则的最小值是( )
A.0B.C.D.
例5-2. (2023·云南昆明·高三昆明一中校考阶段练习)若关于的不等式在上恒成立,则实数的取值范围是____________.
例5-3.(2023·全国·高一专题练习)已知二次函数满足条件:①的解集为;②的最大值为4.
(1)求a,b,c的值;
(2)在区间上,二次函数的图象恒在一次函数图象的下方(无公共点),求实数m的取值范围.
【规律方法】
由不等式恒成立求参数的取值范围的思路及关键
1.一般有两个解题思路:一是分离参数(如例5-1);二是不分离参数.
2.两种思路都是将问题归结为求函数的最值,至于用哪种方法,关键是看参数是否已分离.这两个思路的依据是: (1)a≥f(x)恒成立⇔a≥f(x)max;(2)a≤f(x)恒成立⇔a≤f(x)min..
3.有关二次函数的问题,数形结合,密切联系图象是探求解题思路的有效方法.一般从:①开口方向;②对称轴位置;③判别式;④端点函数值符号四个方面分析.
4. “二次”问题恒成立问题的解题思路
(1)ax2+bx+c>0(a≠0)恒成立的充要条件是eq \b\lc\{\rc\ (\a\vs4\al\c1(a>0,,b2-4ac<0;))
(2)ax2+bx+c<0(a≠0)恒成立的充要条件是eq \b\lc\{\rc\ (\a\vs4\al\c1(a<0,,b2-4ac<0;))
(3)a≥f(x)恒成立⇔a≥f(x)max,a≤f(x)恒成立⇔a≤f(x)min.
【变式训练】
变式5-1.(2023·广西玉林·统考二模)若不等式对恒成立,则a的取值范围是____________.
变式5-2.(2021·全国高三专题练习)设函数.若对于,恒成立,求m的取值范围.
变式5-3.(2020秋·福建泉州·高一晋江市第一中学校考阶段练习)已知关于的不等式的解集是.
(1)求,的值;
(2)若对于任意,不等式恒成立,求实数的取值范围.
题型六:“二次问题”与其它知识的“交汇”
【典例分析】
例6-1.(2023·四川宜宾·统考三模)在中,角A,B,C所对边分别记为a,b,c,若,,则面积的最大值是( )
A.B.2C.D.
例6-2.(2023·全国·高三专题练习)函数的值域是____________.
例6-3.(2023·广西柳州·柳州高级中学校联考模拟预测)双曲线的离心率的取值范围是___.
例6-4.(2023·全国·高三专题练习)设函数,其中为实数.
(1)已知函数在处取得极值,求的值;
(2)已知不等式对都成立,求实数的取值范围.
【规律方法】
1.“三个二次”作为基础知识,应用非常广泛,它与数学的其它知识交汇也很普遍,从近几年高考命题看,命题交汇有:与其它函数函数交汇、与解三角形交汇、与平面向量交汇、与立体几何交汇、与平面解析几何交汇、与导数交汇等.
2.解决“交汇”问题的策略是:先根据所交汇的知识进行变形,通过“换元”转化为用“二次问题”求解,这是难点;
【变式训练】
变式6-1.(2023·宁夏中卫·统考二模)已知点在直线上,若关于的不等式恒成立,则实数的取值范围为( )
A.B.
C.D.
变式6-2.(2023·全国·模拟预测)设,均为正实数,若直线被圆截得的弦长为2,则的取值范围是( )
A.B.
C.D.
变式6-3.(2023·全国·高三专题练习)函数的最小值为________.
变式6-4.(2023·广西柳州·高三柳州高级中学校联考阶段练习)已知函数,若函数在上有极值,则实数a的取值范围为___.
一、单选题
1.(2022秋·福建福州·高一校联考期中)不等式的解集为,则函数的图象为( )
A.B.
C.D.
2.(2023春·黑龙江哈尔滨·高三哈尔滨市第十三中学)对任意的,不等式都成立,则实数a的取值范围是( )
A.B.C.D.
二、多选题
3.(2022秋·安徽合肥·高三合肥一中校考阶段练习)不等式对任意的恒成立,则( )
A.B.C.D.
三、填空题
4.(2023秋·甘肃天水·高一统考期末)若函数在区间上单调递减,则实数a的取值范围是________.
5.(2022秋·四川成都·高三成都七中校考阶段练习)已知函数,方程有两个相等的实数根,若关于的不等式的解集为,则实数的值为________.
6.(2023·贵州黔东南·凯里一中校考三模)正数满足,若不等式恒成立,则实数的取值范围__________.
7.(2023·陕西榆林·统考三模)若不等式对恒成立,则a的取值范围是__________,的最小值为__________.
8.(2023·全国·高三专题练习)已知为正的常数,若不等式对一切非负实数恒成立,则的最大值为________.
9.(2021春·陕西渭南·高一校考阶段练习)如图是二次函数图象的一部分,图象过点,对称轴为.给出下面四个结论:①;②;③;④.其中正确结论的序号是__________.
四、解答题
10.(2023·全国·高三专题练习)已知在区间 上的值域为.
(1)求实数的值;
(2)若不等式 当上恒成立,求实数k的取值范围.
11.(2022秋·山东枣庄·高一统考期末)已知函数,.
(1)若在上单调递减,求实数m的取值范围;
(2)解关于x的不等式.
12.(浙江高考真题)设,若,求证:
(1)方程有实根;
(2);
(3)设是方程的两个实根,则.
解析式
f(x)=ax2+bx+c(a>0)
f(x)=ax2+bx+c(a<0)
图象
定义域
(-∞,+∞)
(-∞,+∞)
值域
eq \b\lc\[\rc\)(\a\vs4\al\c1(\f(4ac-b2,4a),+∞))
eq \b\lc\(\rc\](\a\vs4\al\c1(-∞,\f(4ac-b2,4a)))
单调性
在eq \b\lc\(\rc\](\a\vs4\al\c1(-∞,-\f(b,2a)))上单调递减;
在eq \b\lc\[\rc\)(\a\vs4\al\c1(-\f(b,2a),+∞))上单调递增
在eq \b\lc\(\rc\](\a\vs4\al\c1(-∞,-\f(b,2a)))上单调递增;
在eq \b\lc\[\rc\)(\a\vs4\al\c1(-\f(b,2a),+∞))上单调递减
对称性
函数的图象关于x=-eq \f(b,2a)对称
设f(x)=ax2+bx+c(a>0),方程ax2+bx+c=0的判别式Δ=b2-4ac
判别式Δ
=b2-4ac
Δ>0
Δ=0
Δ<0
解不等式
f(x)>0
或f(x)<0
的步骤
求方程f(x)=0的解
有两个不等的实数解x1,x2
有两个相等的实数解x1=x2
没有实数解
画函数y=f(x)的示意图
不等式
的解集
f(x)>0
{x|x
{x|x≠-eq \f(b,2a)}
R
f(x)<0
{x|x1
∅
专题4.4 导数与不等式-2024年高考数学大一轮复习核心考点精讲精练(新高考专用): 这是一份专题4.4 导数与不等式-2024年高考数学大一轮复习核心考点精讲精练(新高考专用),文件包含专题44导数与不等式原卷版docx、专题44导数与不等式解析版docx等2份试卷配套教学资源,其中试卷共51页, 欢迎下载使用。
专题3.9 函数的实际应用-2024年高考数学大一轮复习核心考点精讲精练(新高考专用): 这是一份专题3.9 函数的实际应用-2024年高考数学大一轮复习核心考点精讲精练(新高考专用),文件包含专题39函数的实际应用原卷版docx、专题39函数的实际应用解析版docx等2份试卷配套教学资源,其中试卷共50页, 欢迎下载使用。
专题3.8 函数与方程-2024年高考数学大一轮复习核心考点精讲精练(新高考专用): 这是一份专题3.8 函数与方程-2024年高考数学大一轮复习核心考点精讲精练(新高考专用),文件包含专题38函数与方程原卷版docx、专题38函数与方程解析版docx等2份试卷配套教学资源,其中试卷共43页, 欢迎下载使用。