2023-2024学年山东省青岛市李沧区九年级（上）期末数学试卷（含解析）

这是一份2023-2024学年山东省青岛市李沧区九年级（上）期末数学试卷（含解析），共23页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.2024年1月4日，第22届瓦萨国际滑雪节开幕式在长春净月潭国家森林公园启幕.如图，一名滑雪运动员沿着倾斜角为α的斜坡，从点A滑行到点B.若AB=500m，则这名滑雪运动员下降的高度为( )
A. 500sinαm
B. 500csαm
C. 500tanαm
D. 500tanαm
2.如图是一把做工精湛的紫砂壶，其俯视图的大致形状是( )
A.
B.
C.
D.
3.小明拿一个等边三角形木框在阳光下玩，等边三角形木框在地上的投影不可能是( )
A. 线段B. 一个点C. 等边三角形D. 等腰三角形
4.如图是一把直角三角尺，∠C=90°，∠B=30°，AC=7cm，DF=5cm，且△ABC∽△DFE，则这把三角尺中△ABC与△DFE的周长比为( )
A. 7：5
B. 49：25
C. 14：5
D. 196：25
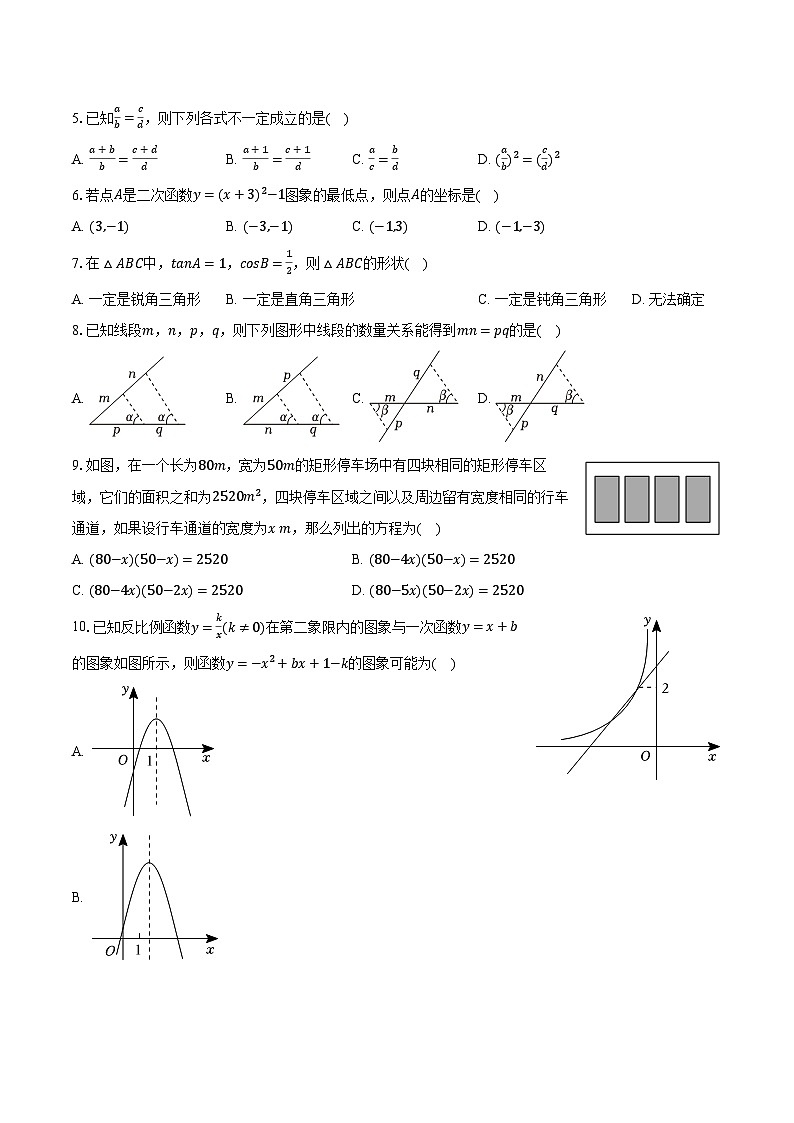
5.已知ab=cd，则下列各式不一定成立的是( )
A. a+bb=c+ddB. a+1b=c+1dC. ac=bdD. (ab)2=(cd)2
6.若点A是二次函数y=(x+3)2−1图象的最低点，则点A的坐标是( )
A. (3,−1)B. (−3,−1)C. (−1,3)D. (−1,−3)
7.在△ABC中，tanA=1，csB=12，则△ABC的形状( )
A. 一定是锐角三角形B. 一定是直角三角形C. 一定是钝角三角形D. 无法确定
8.已知线段m，n，p，q，则下列图形中线段的数量关系能得到mn=pq的是( )
A. B. C. D.
9.如图，在一个长为80m，宽为50m的矩形停车场中有四块相同的矩形停车区域，它们的面积之和为2520m2，四块停车区域之间以及周边留有宽度相同的行车通道，如果设行车通道的宽度为x m，那么列出的方程为( )
A. (80−x)(50−x)=2520B. (80−4x)(50−x)=2520
C. (80−4x)(50−2x)=2520D. (80−5x)(50−2x)=2520
10.已知反比例函数y=kx(k≠0)在第二象限内的图象与一次函数y=x+b的图象如图所示，则函数y=−x2+bx+1−k的图象可能为( )
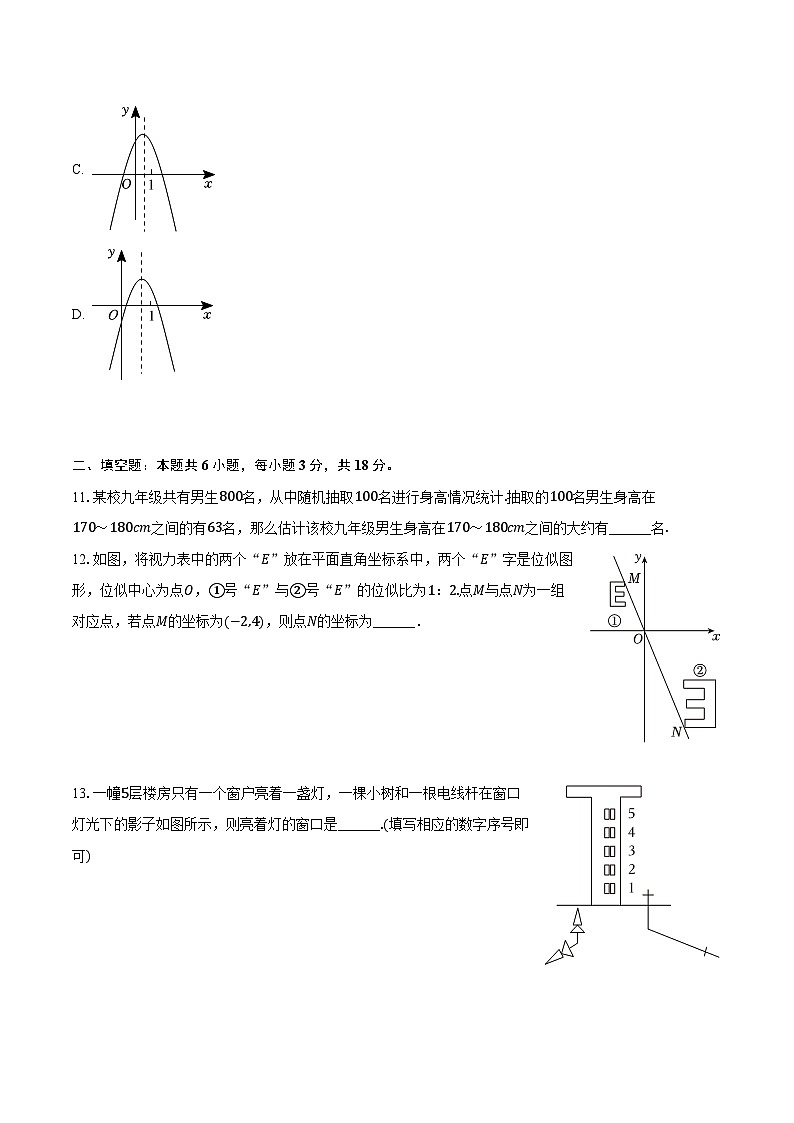
A.
B.
C.
D.
二、填空题：本题共6小题，每小题3分，共18分。
11.某校九年级共有男生800名，从中随机抽取100名进行身高情况统计.抽取的100名男生身高在170～180cm之间的有63名，那么估计该校九年级男生身高在170～180cm之间的大约有______名.
12.如图，将视力表中的两个“E”放在平面直角坐标系中，两个“E”字是位似图形，位似中心为点O，①号“E”与②号“E”的位似比为1：2.点M与点N为一组对应点，若点M的坐标为(−2,4)，则点N的坐标为______．
13.一幢5层楼房只有一个窗户亮着一盏灯，一棵小树和一根电线杆在窗口灯光下的影子如图所示，则亮着灯的窗口是______.(填写相应的数字序号即可)
14.如图，在菱形ABCD中，点E为对角线AC上一点，且AE=AD，连接DE，若AB=10，AC=16，则DE的长为______．
15.已知关于x的方程2x2+kx−10=0的一个根为x=5，则另一个根为______．
16.如图，在正方形ABCD中，点E为边BC的中点，AE交BD于点F，过点D作DG⊥AE于点G，则S△DAG：S△DFG= ______．
三、解答题：本题共9小题，共72分。解答应写出文字说明，证明过程或演算步骤。
17.(本小题4分)
已知：线段a．
求作：矩形ABCD，使得AB=a，AC=2a．
18.(本小题8分)
(1)解方程：x2−10x−7=0．
(2)已知关于x的一元二次方程(m−2)x2−3x+2=0有实数根，求m的取值范围．
19.(本小题6分)
杭州亚运会吉祥物是一组承载深厚底蕴和充满时代活力的机器人，组合名为“江南忆”，出自唐朝诗人白居易的名句“江南忆，最忆是杭州”，它融合了杭州的历史人文、自然生态和创新基因.现有三张不透明的卡片，其正面图案分别为杭州亚运会吉祥物“宸宸”、“琮琮”、“莲莲”图案(卡片依次记为A，B，C)，卡片除正面图案不同外，其余均相同.现将这三张卡片背面向上洗匀，从中随机抽取一张，记录图案后放回，重新洗匀后再从中随机抽取一张.请用画树状图(或列表)的方法，求两次抽出的卡片上的图案都是“宸宸”的概率．
20.(本小题8分)
如图，某小区有南北两个门，北门A在南门B的正北方向，小红自小区北门A处出发，沿南偏西53°方向前往小区居民活动中心C处；小强自南门B处出发，沿正西方向行走300m到达D处，再沿北偏西30°方向前往小区居民活动中心C处与小红汇合，两人所走的路程相同，求该小区北门A与南门B之间的距离.(结果保留整数，参考数据：sin53°≈0.8，cs53°≈0.6，tan53°≈1.3 3≈1.73)
21.(本小题8分)
如图，一次函数y=kx+b的图象与反比例函数y=−6mx的图象相交于点A(m+2,6)和点B(−3,m−1)，与x轴交于点C，与y轴交于点D．
(1)求反比例函数与一次函数的关系式；
(2)根据图象直接写出−6mx0，反比例函数y=的图象经过第二、四象限，则k0，1−k>0，从而排除A、D，在B、C两个选项中选择，又由题意，反比例函数y=与一次函数y=x+b的图象有两个交点，其中一个交点纵坐标为2，k2+b=2，进而可得2−b=k21，故可得解．
本题主要考查的是一次函数、反比例函数和二次函数的图象，应该熟记一次函数、反比例函数和二次函数在不同情况下所在的象限．
11.【答案】504
【解析】解：∵抽取的100名男生身高在170～180cm之间的有63名．
∴九年级男生身高在170～180cm之间的大约有800×63100=504(名)．
故答案为：504．
用九年级男生总数乘以身高在170～180cm之间的男生所占的百分比即可得出答案．
本题考查了用样本估计总体，掌握用样本估计总体的方法是解题的关键．
12.【答案】(4,−8)
【解析】解：∵点M与点N为一组对应点，若点M的坐标为(−2,4)，相似比为1：2，
∴N(4,−8)．
故答案为：(4,−8)．
利用位似变换的性质求解即可．
本题考查位似变换，坐标确定位置等知识，解题的关键是掌握位似变换的性质．
13.【答案】3
【解析】解：如图，点O即为所求，投影中心在3号窗口．
故答案为：3．
根据中心投影的定义，画出图形即可．
本题考查中心投影，解题的关键是正确作出投影中心的位置，属于中考常考题型．
14.【答案】2 10
【解析】解：连接DB，交AC于点F，
∵四边形ABCD是菱形，
∴AC⊥BD，AF=CF，
∵AB=10，
∴AD=AE=AB=10，
∵AC=16，
∴AF=CF=8，
在Rt△ADF中，AD=10，AF=8，
根据勾股定理得：DF=6，
∵AE=10，AF=8，
∴EF=AE−AF=10−8=2，
在Rt△DEF中，DF=6，EF=2，
根据勾股定理得：DE= DF2+EF2=2 10，
故答案为：2 10，
连接DB，根据菱形的性质得出AD=AE=AB=10，AF=CF=8，根据线段的和差关系求出EF的值，再利用勾股定理解答即可．
本题主要考查了菱形的性质和勾股定理，熟练掌握相关性质是解答本题的关键．
15.【答案】x=−1
【解析】解：设此方程的另一根为m，
由一元二次方程根与系数的关系得：5m=−102=−5，
解得m=−1，
即方程的另一根为x=−1，
故答案为：x=−1．
本题根据x1⋅x2=ca，即可得到答案．
本题考查了一元二次方程根与系数的关系，熟练掌握一元二次方程根与系数的关系是解题关键．
16.【答案】3：2
【解析】解：∵点E为边BC的中点，
∴BE=12BC，
∵四边形ABCD为正方形，
∴BC/​/AD，BC=AD，
∴BE=12AD．
∵BC/​/AD，
∴△BEF∽△DAF，
∴EFAF=BEAD=12，S△BEFS△DAF=(BEAD)2=14，
设S△BEF=a，则S△DAF=4a，S△ABF=2S△BEF=2a．
∴S△ABE=3a．
设BE=k，则AB=AD=2k，
∴AE= AB2+BE2= 5k.
∵AD/​/BE，
∴∠DAG=∠AEB，
∵∠AGD=∠ABE=90°，
∴△AGD∽△EBA，
∴S△AGDS△EBA=(ADAE)2=(2k 5k)2=45，
∴S△AGD=45×3a=125a，
∴S△DGF=S△DAF−S△DAG=4a−125a=85a，
∴S△DAG：S△DFG=125a：85a=3：2．
故答案为：3：2．
利用正方形的性质和相似三角形的判定与性质得到△BEF∽△DAF，它们面积的比为1：4，设S△BEF=a，则S△DAF=4a，S△ABF=2S△BEF=2a，S△ABE=3a；利用相似三角形的判定与性质得到△AGD∽△EBA，它们面积的比为4：5，分别计算得到S△DAG，S△DFG，则结论可求．
本题主要考查了正方形的性质，勾股定理，相似三角形的判定与性质，熟练掌握正方形的性质和相似三角形的判定与性质是解题的关键．
17.【答案】解：如图，矩形ABCD为所作．

【解析】先再直线l上截取AD=2a，再过A点作直线l的垂线，接着在垂线上截取AB=a，然后分别以B点、D点为圆心，AD为半径或AB的长画弧两弧相交于点C，则四边形ABCD满足条件．
本题考查了作图−复杂作图：解决此类题目的关键是熟悉基本几何图形的性质，结合几何图形的基本性质把复杂作图拆解成基本作图，逐步操作．
18.【答案】解：(1)x2−10x−7=0，
x2−10x=7，
x2−10x+25=7+25，即(x−5)2=32，
∴x−5=±4 2，
∴x1=5+4 2，x2=5−4 2；
(2)∵关于x的一元二次方程(m−2)x2−3x+2=0有实数根，
∴△≥0，
即Δ=b2−4ac=(−3)2−4(m−2)×2
=9−8m+16
=−8m+16≥0，
∴m≤2，
∵此方程是一元二次方程，
∴m−2≠0，即m≠2．
∴m的取值范围是：m