北师大版八年级下册2 平行四边形的判定课文内容课件ppt

这是一份北师大版八年级下册2 平行四边形的判定课文内容课件ppt，共19页。PPT课件主要包含了教学目标，重难点，导入新课，要如何证明呢，探究新知，归纳新知，典型例题，∵AECF，即EOFO，∴AD∥BC等内容，欢迎下载使用。

1.理解对角线互相平分的四边形是平行四边形这一判定定理
2.理解两组对角分别相等的四边形是平行四边形，并学会简单运用
1.平行四边形判定方法的综合运用
2.平行四边形判定方法的综合运用
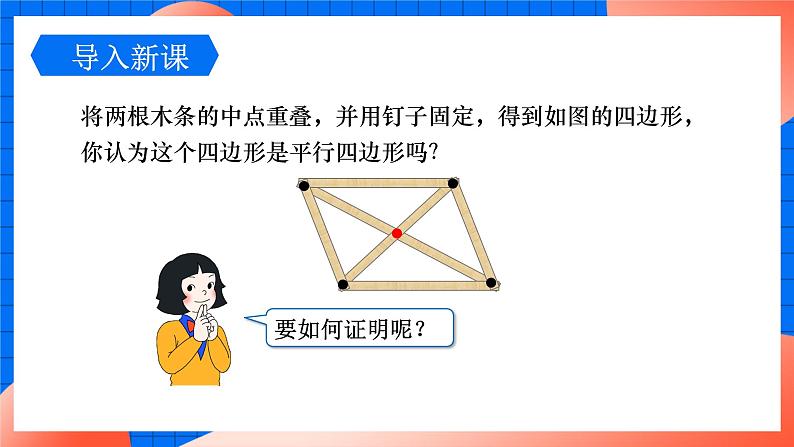
将两根木条的中点重叠，并用钉子固定，得到如图的四边形，你认为这个四边形是平行四边形吗？
已知：如图，四边形ABCD的两条对角线AC与BD相交于点O，并且OA=OC，OB=OD.求证：四边形ABCD是平行四边形.
证明：∵OA=OC，OD=OB，∠AOD=∠COB，∴△AOD≌ △COB.∴AD=CB，∠ADO=∠CBO.∴AD∥CB.∴四边形ABCD是平行四边形（一组对边平行且相等的四边形是平行四边形）.
定理 对角线互相平分的四边形是平行四边形.
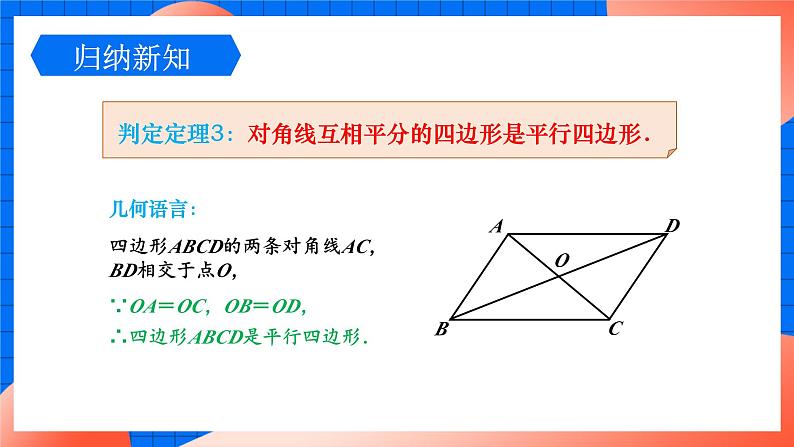
判定定理3：对角线互相平分的四边形是平行四边形．
四边形ABCD的两条对角线AC，BD相交于点O，
∵OA＝OC，OB＝OD，∴四边形ABCD是平行四边形．
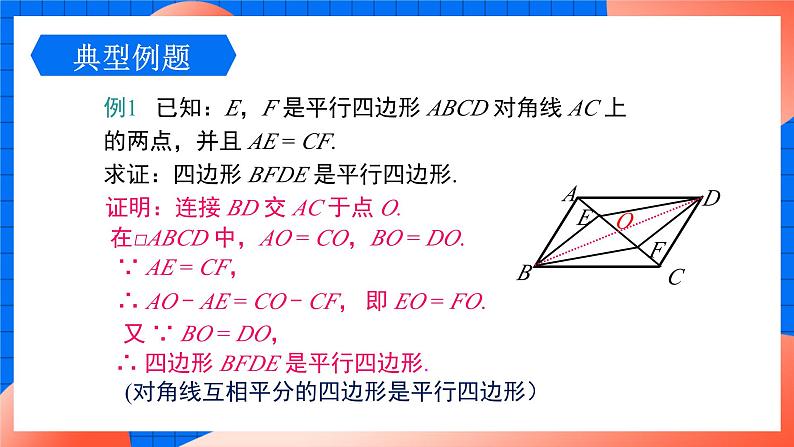
例1 已知：E，F 是平行四边形 ABCD 对角线 AC 上的两点，并且 AE = CF.求证：四边形 BFDE 是平行四边形.
证明：连接 BD 交 AC 于点 O.
在□ABCD 中，AO = CO，BO = DO.
∴ AO - AE = CO - CF，
又 ∵ BO = DO，
∴ 四边形 BFDE 是平行四边形.
(对角线互相平分的四边形是平行四边形）
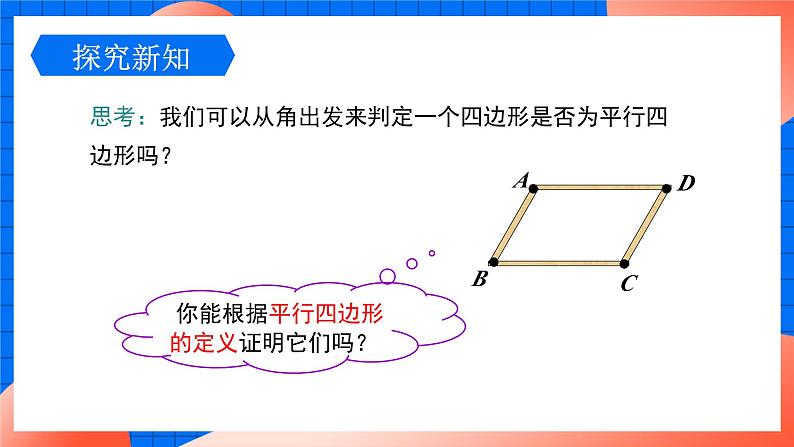
思考：我们可以从角出发来判定一个四边形是否为平行四边形吗？
你能根据平行四边形的定义证明它们吗？
已知：四边形 ABCD 中，∠A =∠C，∠B =∠D.求证：四边形 ABCD 是平行四边形.
又∠A =∠C，∠B =∠D，
∵∠A +∠C +∠B +∠D = 360°，
∴ 2∠A + 2∠B = 360°，
即∠A +∠B = 180°.
∴ 四边形 ABCD 是平行四边形.
定义判定：两组对角分别相等的四边形是平行四边形
1.两组对边分别平行的四边形是平行四边形
2.两组对边分别相等的四边形是平行四边形
3.一组对边平行且相等的四边形是平行四边形
两组对角分别相等的四边形是平行四边形
两条对角线互相平分的四边形是平行四边形
解：有 6 个平行四边形，分别是：　 □ ABOF，□ ABCO， □ BCDO，□ CDEO， □ DEFO，□ EFAO．
小明用手中六个全等的正三角形做拼图游戏时，拼成一个六边形．你能在图中找出所有的平行四边形吗？并说说你的理由．
1．如图，在四边形ABCD中，对角线AC，BD相交于点O，下列条件不能判定四边形ABCD为平行四边形的是(　　) A．AB∥CD，AD∥BC B．OA＝OC，OB＝OD C．AD＝BC，AB∥CD D．AB＝CD，AD＝BC
2.判断下列说法是否正确(1)一组对边平行且另一组对边相等的四边形是平行四边形.( )(2)两组对角都相等的四边形是平行四边形. ( )
(3)一组对边平行且一组对角相等的四边形是平行四边形. ( )(4)一组对边平行,一组邻角互补的四边形是平行四边形. ( )
3.如图，在□ ABCD中，对角线AC与BD相交于点O，点E，F分别是OA和OC的中点，四边形BFDE是平行四边形吗？请说明理由.
4. 如图，在四边形 ABCD 中，AB∥CD，E 是 BC 的中点，直线 AE 交 DC 的延长线于点 F．试判断四边形 ABFC 的形状，并证明你的结论．
解：四边形 ABFC 是平行四边形. 证明如下：∵ AB∥CD，∴∠BAE =∠CFE.∵ E 是 BC 的中点，∴ BE = CE. 在△ABE 和△FCE 中，
∴△ABE≌△FCE（AAS）. ∴ AE = EF. 又∵ BE = CE∴ 四边形 ABFC 是平行四边形．
两组对边分别平行的四边形是平行四边形(定义法)
两组对边分别相等的四边形是平行四边形(判定定理1)
一组对边平行且相等的四边形是平行四边形（判定定理2）
两组对角分别相等的四边形是平行四边形（定义拓展）
对角线互相平分的四边形是平行四边形（判定定理3）