江苏省扬州市广陵区2023-2024学年八年级上学期期末数学试题

这是一份江苏省扬州市广陵区2023-2024学年八年级上学期期末数学试题，共13页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。

友情提醒：本卷中的所有题目均在答题卷上作答，在本卷中作答无效．
一、选择题（本大题共8小题，每小题3分，共24分，在每小题所给出的四个选项中，恰有一项是符合题目要求的，请将正确选项前的字母代号填涂在答题卷相应位置上）
1．杭州亚运会给世界带来了一场展示体育精神和亚洲团结的盛会，下列关于体育运动的图标中，是轴对称图形的是（ ）
A．B．C．D．
2．在实数中是无理数的有（ ）
A．2个B．3个C．4个D．5个
3．下列各式计算正确的是（ ）
A．B．C．D．
4．一次函数的图象经过第一、三、四象限，则化简所得的结果是（ ）
A．B．C．D．
5．已知点都在直线上，则的大小关系是（ ）
A．B．C．D．
6．如图，已知，那么添加下列一个条件后，不能判定的是（ ）
（第6题）
A．B．C．D．
7．如图，在平面直角坐标系中，已知，点的坐标分别是则点的坐标是（ ）
（第7题）
A．B．C．D．
8．如图，四边形中，，在上分别找一点、，使周长最小时，则的度数为（ ）
（第8题）
A．B．C．D．
二、填空题（本大题共10题，每题3分，共30分．不需写出解答过程，请把答案直接填写在答题卷相应位置上）
9．已知一个正数的两个平方根分别是和，则这个正数等于______．
10．在中，是斜边上的中线，如果，那么______．
11．等腰三角形的一个内角是，则它的底角度数是______．
12．扬州中国大运河博物馆占地200亩，总建筑面积79373.59平方米，主体由博物馆和大运塔两部分组成．将数字79373.59精确到千位并用科学记数法表示的结果为______．
13．已知点与点关于轴对称，则点的坐标为______．
14．设为实数，已知，则______．
15．将直线向上平移3个单位后经过点，则的值为______．
16．如图，在直角坐标系中，的顶点在轴上，顶点在轴上，，，点的坐标为，点和点关于成轴对称，且交轴于点．则点的坐标为______．
（第16题）
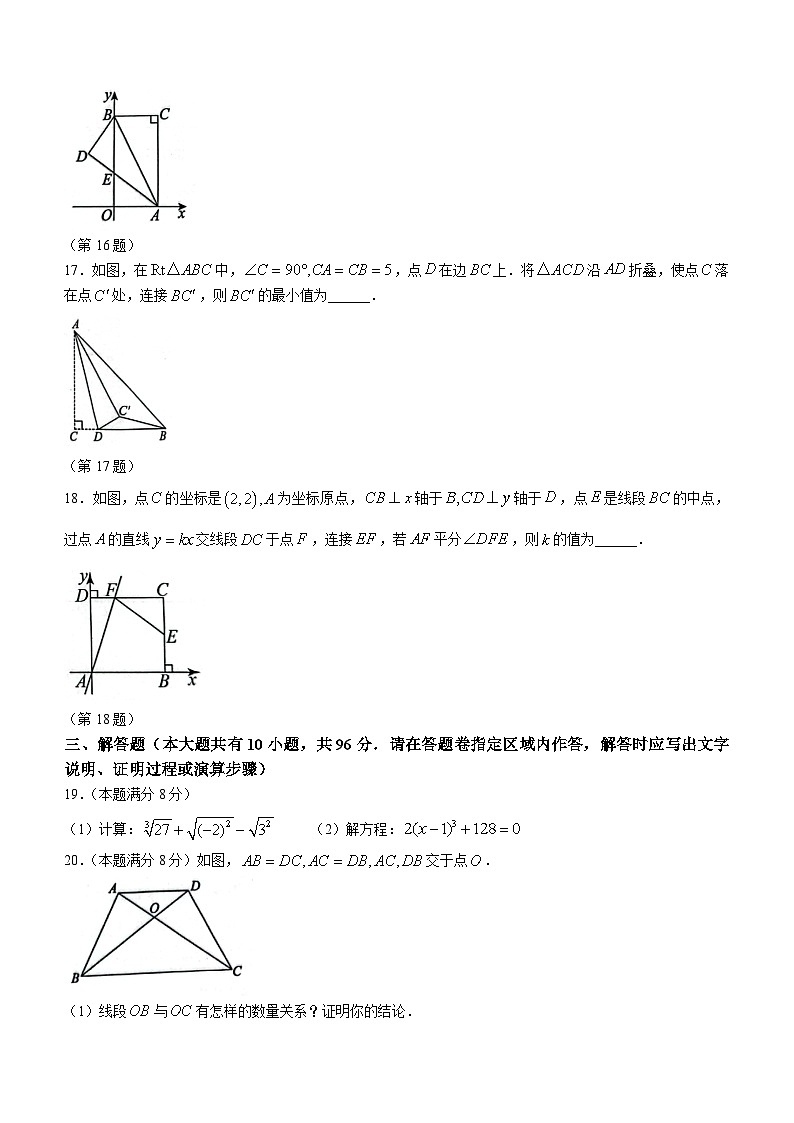
17．如图，在中，，点在边上．将沿折叠，使点落在点处，连接，则的最小值为______．
（第17题）
18．如图，点的坐标是为坐标原点，轴于轴于，点是线段的中点，过点的直线交线段于点，连接，若平分，则的值为______．
（第18题）
三、解答题（本大题共有10小题，共96分．请在答题卷指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）
19．（本题满分8分）
（1）计算： （2）解方程：
20．（本题满分8分）如图，交于点．
（1）线段与有怎样的数量关系？证明你的结论．
（2）与有怎样的数量关系？证明你的结论．
21．（本题满分8分）在由单位正方形（每个小正方形边长都为1）组成的网格中，的顶点均在格点上．
（1）把向左平移4个单位，再向上平移2个单位得到，请画出，并写出点的坐标；
（2）请画出关于轴对称的，并求出的面积．
22．（本题满分8分）如图，折叠长方形纸片，使点落在边上的点处，折痕为．已知．求的长．
23．（本题满分10分）已知一次函数，它的图像与两坐标轴所围成的图形的面积等于2．
（1）求的值；
（2）若函数的图象交轴于正半轴，则当取何值时，的值是正数？
24．（本题满分10分）甲、乙两家草莓采摘园的草莓品质相同，销售价格也相同．新春佳节，两家均推出了优惠方案，甲采摘园的优惠方案：游客进园需购买60元的门票，采摘的草莓六折优惠；乙采摘园的优惠方案：游客进园不需购买门票，采摘的草莓超过一定数量后，超过部分打折优惠．优惠期间，设某游客的草莓采摘量为（千克），在甲采摘园所需总费用为（元），在乙采摘园所需总费用为（元），图中折线表示与之间的函数关系．
（1）求与之间的函数关系式；
（2）当游客采摘15千克的草莓时，你认为他在哪家草莓园采摘更划算？为什么？
25．（本题满分10分）如图，在中，是的角平分线，于，点在边上，连接．
（1）求证：；
（2）若，试说明与的数量关系；
（3）在（2）的条件下，若，则的长为______．（用含的代数式表示）
26．（本题满分10分）如图，已知直线交轴于，交轴于．
（1）求直线向右平移2个单位得到的直线的函数表达式；
（2）求直线关于对称的直线的函数表达式；
（3）点在直线上，若，求点坐标．
27．（本题满分12分）如图，在中，平分交斜边于点，动点从点出发，沿折线向终点运动．
（1）点在上运动的过程中，当______时，与的面积相等；
（2）点在折线上运动的过程中，若是等腰三角形，求的度数；
（3）若点是斜边的中点，当动点在上运动时，线段所在直线上存在另一动点，使两线段的长度之和，即的值最小，则此______．（直接写出答案）
28．（本题满分12分）如图①，直线分别与轴交于两点，过点的直线交轴负半轴于点．
图①图②
（1）求直线的函数表达式．
（2）在直线上是否存在点，使得？若存在，求出点坐标：若不存请说明理由；
（3）如图②，为轴正半轴上的一动点，以为直角顶点、为腰在第一象限内作等腰直角三角形，连接．请直接写出的最大值．
2023—2024学年八年级第一学期期末考试数学试卷
参考答案及评分标准
一、选择题（本大题共8小题，每小题3分，共24分）
二、填空题（本大题共10小题，每小题3分，共30分）
9．9 10．4.8 11．40 12． 13．
14． 15．2 16． 17． 18．1或3
三、解答题（本大题共102分）
19．（1）解：原式．
（2）解：
20．，
证明：在和中
．
21．解：（1）如图，即为所求．
点的坐标为．
（2）如图，即为所求．
的面积为．
22．解：由折叠而来，．
在中，，
，．
设，则，
在中，，即，
解得：．
23．解：（1）当时，，
一次函数图象与轴的交点坐标为；
当时，，
一次函数图象与轴的交点坐标为．
，解得：．
（2）函数的图象交轴于正半轴，
一次函数为，的值是正数，，
解得．
故当时，的值是正数．
24．解：（1）根据题意得，甲、乙两采摘园优惠前的草莓销售价格：（元/千克）．
；
当时，；当时，设，
由题意的：，解得，
，
与之间的函数关系式为：
（2）当时，，，
，他在甲家草莓园采摘更划算．
25．（1）证明：，，
在和中，
，；
（2）解：．
理由：由（1）得：，，
在和中，，
，．
，；
（3）解：由（2）知，，，
由（1）知．，．
，．
，．
故答案为：
26．解：（1）直线向右平移2个单位得到的直线的函数表达式为，即，
故答案为；
（2）在直线上，
这两点关于的对称点为，
设直线的解析式为，
，解得，
直线的解析式为：，
故答案为；
（3）直线交轴于，交轴于．
，，
设的坐标为，，
，即，
解得或2，或．
27．解：（1）解：当时，与的面积相等理由如下：
，
平分，，
在和中，
与的面积相等．
（2）由（1）得：，
分两种情况：
①点在上，如图1所示：
图1
若，则，
；
若时，则，
若，；
①点在上时，如图2所示：
图2
存在，，
，，
，
；
综上所述，的度数为或或或．
（3）当在上，且时，最小，作于，如图3所示：
图3
则，平分，，
又，
，，
当点三点共线时，的值最小，则，，
，
点是斜边的中点，
28．解：（1）直线分别与轴交于两点，令，则，
，且
设直线的解析式为，
，解得，，
直线的解析式为
（2）解：由（1）可知直线的解析式为，直线的解析式为，
，
，
如图所示，点在直线上，过点作轴于，
设，
，，
，
①当，即时，
，
若，则，解得，则；
②当，即时，
，
若，则，解得，（舍去）；
③当，即时，
，
若，则，解得，
则；
综上所述，当或时，；
（3）解：已知，设，
在中，，
是等腰直角三角形，，
如图所示，过点作轴于，
在，中，
，
，，
，，
，，且轴，
是等腰直角三角形，，
则点的轨迹在射线上，
如图所示，作点关于直线的对称点，
连接，
是等腰直角三角形，即，根据对称性质，，
轴，且，
，则，
如图所示，当点在一条直线上时，的值最大，最大值为的值；
由勾股定理得：，
故答案为：．题号
1
2
3
4
5
6
7
8
答案
C
C
B
D
A
C
D
B