初中数学北师大版八年级下册3 线段的垂直平分线教学演示ppt课件

这是一份初中数学北师大版八年级下册3 线段的垂直平分线教学演示ppt课件，共17页。PPT课件主要包含了学习目标，做一做，新课导入，概念剖析，即PAPB，垂直平分线的性质，垂直平分线的判定，归纳总结，典型例题，∵AE5cm等内容，欢迎下载使用。

1.掌握线段垂直平分线的性质定理和判定定理（重点）2.会用线段垂直平分线的性质解决问题
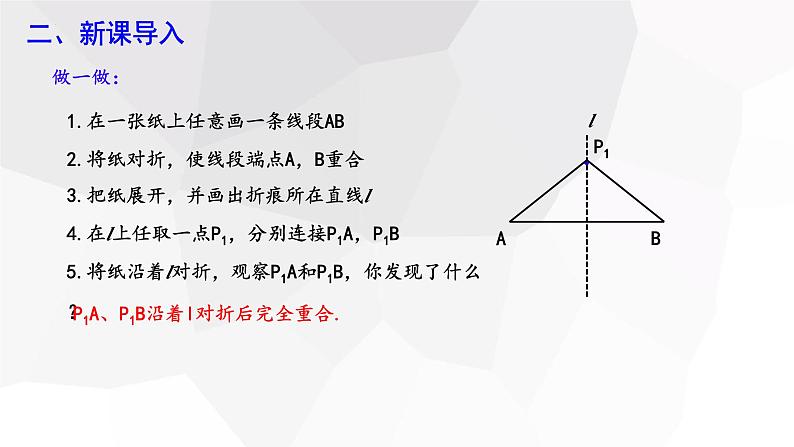
1.在一张纸上任意画一条线段AB2.将纸对折，使线段端点A，B重合3.把纸展开，并画出折痕所在直线l4.在l上任取一点P1，分别连接P1A，P1B5.将纸沿着l对折，观察P1A和P1B，你发现了什么？
P1A、P1B沿着l对折后完全重合.
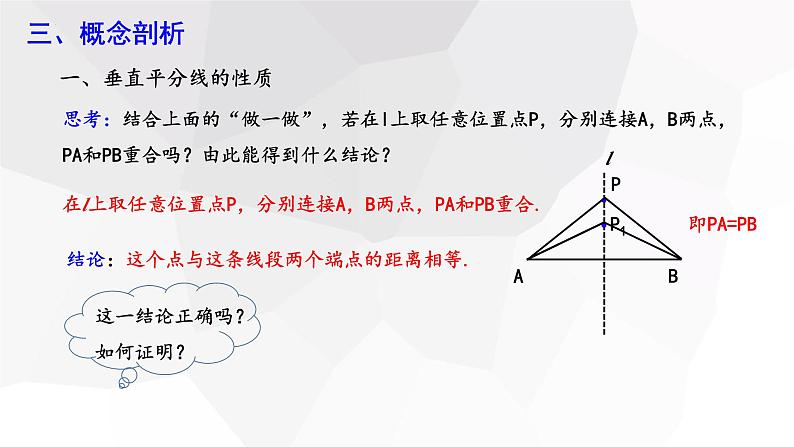
思考：结合上面的“做一做”，若在l上取任意位置点P，分别连接A，B两点，PA和PB重合吗？由此能得到什么结论？
在l上取任意位置点P，分别连接A，B两点，PA和PB重合.
结论：这个点与这条线段两个端点的距离相等.
这一结论正确吗？如何证明？
结合判定三角形全等的方法，我们来证明这个结论是否正确.
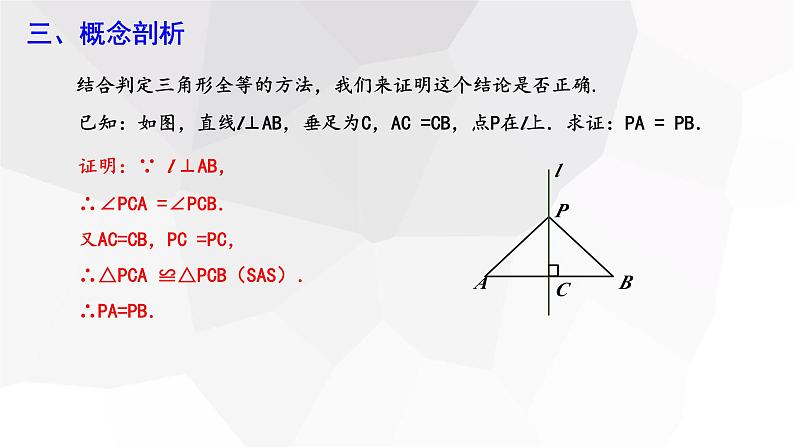
已知：如图，直线l⊥AB，垂足为C，AC =CB，点P在l上．求证：PA = PB．
证明：∵ l ⊥AB，∴∠PCA =∠PCB．又AC=CB，PC =PC，∴△PCA ≌△PCB（SAS）．∴PA=PB．
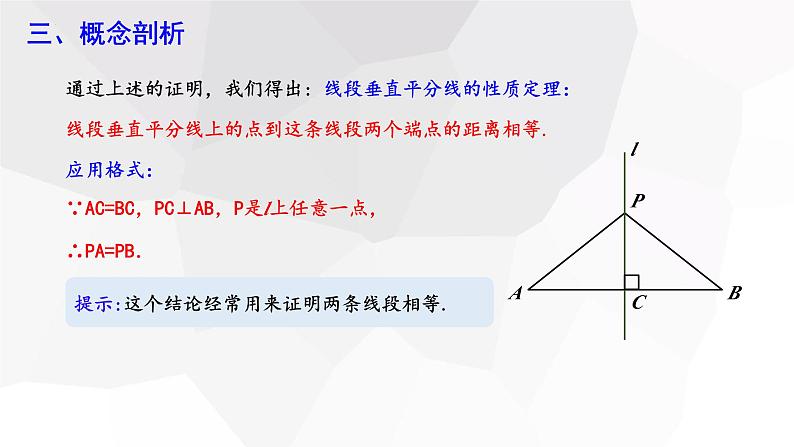
通过上述的证明，我们得出: 线段垂直平分线的性质定理：线段垂直平分线上的点到这条线段两个端点的距离相等.应用格式：∵AC=BC，PC⊥AB，P是l上任意一点，∴PA=PB．
提示:这个结论经常用来证明两条线段相等.
思考：“线段垂直平分线上的点到这条线段两个端点的距离相等”的逆命题是什么？
到线段两个端点距离相等的点在这条线段的垂直平分线上.
它是一个真命题吗？如何证明？
要证明这个命题需要以下步骤：写出已知、求证，作出图形.
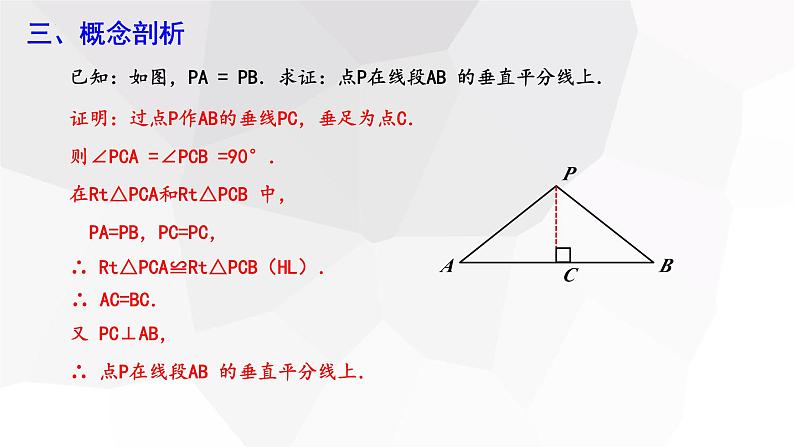
已知：如图，PA = PB．求证：点P在线段AB 的垂直平分线上．
证明：过点P作AB的垂线PC，垂足为点C．则∠PCA =∠PCB =90°．
在Rt△PCA和Rt△PCB 中， PA=PB，PC=PC，
∴ Rt△PCA≌Rt△PCB（HL）．
又 PC⊥AB，∴ 点P在线段AB 的垂直平分线上．
通过上述的证明，我们得出线段垂直平分线的判定定理：与线段两个端点距离相等的点在这条线段的垂直平分线上.应用格式：∵PA=PB，∴点P在AB的垂直平分线上．
提示:这个结论经常用来证明点在直线上(或直线经过某一点).
1.线段的垂直平分线可以看作是到这条线段的两个端点距离相等的所有点的集合.2.线段垂直平分线上的点与这条线段两个端点的距离相等.3.与线段两个端点距离相等的点，在这条线段的垂直平分线上.
例1.△ABC中，DE是AC的垂直平分线，AE=5cm，△CBD的周长为24cm，求△ABC的周长．
分析：根据线段垂直平分线的性质得到CD=AD，AE=CE，根据三角形的周长公式计算．
解：∵DE是AC的垂直平分线
∴ CD=AD，AE=CE，
∴AC=2AE=10cm，
∴ BC+CD+BD=24，
∴BC+AD+BD=24，
∴△ABC的周长=AC+AB+BC=10+24=34cm．
1.如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC=6，AC=5，则△ACE的周长为（　　）A．8 B．11 C．16 D．17
分析：应用线段垂直平分线的性质定理，垂直平分线上的点到线段的两个端点距离相等，从而把三角形的边进行转移，求得周长．
2.如图，在Rt△ABC中，∠B=90°，ED是AC的垂直平分线，交AC于点D，交BC于点E．已知∠BAE=10°，求∠C的度数．
解：∵∠B=90°，∠BAE=10°，∴∠BEA=80°．∵ED是AC的垂直平分线，∴AE=EC，△AED≌△CED（SSS）∴∠C=∠EAC，∵∠BEA=∠C+∠EAC，∴∠C=40°．
例2.已知：如图，点E是∠AOB的平分线上一点，EC⊥OA,ED⊥OB,垂足分别为C,D，连接CD. 求证：OE是CD的垂直平分线.
证明：∵OE平分∠AOB,EC⊥OA,ED⊥OB，
∴∠DOE=∠COE,∠ODE=∠OCE
又∵OE=OE，∴△OED≌△OEC（AAS)∴OD=0C，DE=CE,∴ OE是CD的垂直平分线.
注意：证明一条直线是一条线段的垂直平分线时，必须同时证明这条直线上的两点都在线段的垂直平分线上.
3.如图所示，AC=AD,BC=BD,则下列说法正确的是（　　）A．AB垂直平分CDB．CD垂直平分AB C．AB与CD互相垂直平分D．CD平分∠ACB
4.已知：如图，PA = PB．求证：点P在线段AB 的垂直平分线上．
证明:取AB的中点C，连接PC.∵AC=BC，PA=　 　，PC=　 　， ∴△PCA≌　 　(SSS)， ∴∠PCA=∠PCB=　 　. 
请补全下面的证明过程：
即直线 l 垂直AB并且通过AB的中点C，所以点P在线段AB的垂直平分线上.