沪科版七年级下册10.1 相交线教案配套ppt课件

这是一份沪科版七年级下册10.1 相交线教案配套ppt课件，共14页。PPT课件主要包含了学习目标，新课导入，概念剖析，对顶角的定义，典型例题，只有D项符合，当堂检测，根据顶角的定义，观察图形可知等内容，欢迎下载使用。
1.知道对顶角的概念，能判断两个角是否为对顶角；2.掌握“对顶角相等”的性质，能运用该性质进行有关角度 的计算.(重点)
观察：你能根据图中的提示画出相交线吗？
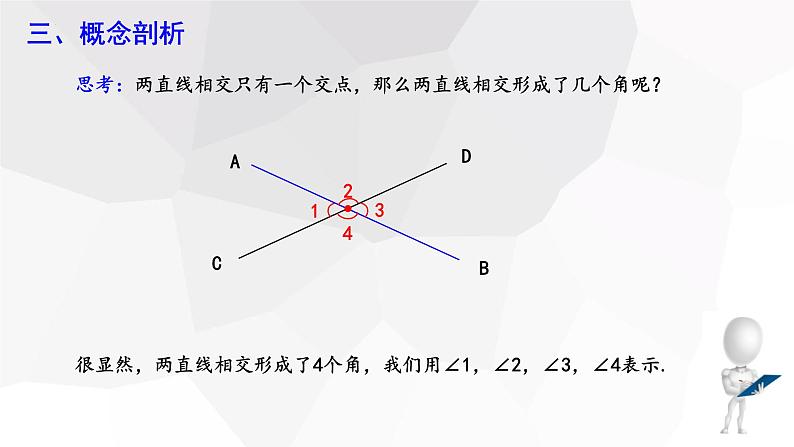
思考：两直线相交只有一个交点，那么两直线相交形成了几个角呢？
很显然，两直线相交形成了4个角，我们用∠1，∠2，∠3，∠4表示.
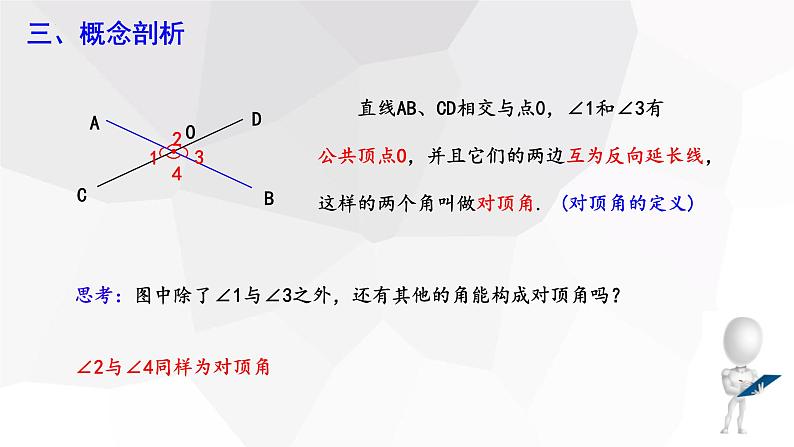
直线AB、CD相交与点0，∠1和∠3有公共顶点O，并且它们的两边互为反向延长线，这样的两个角叫做对顶角.
思考：图中除了∠1与∠3之外，还有其他的角能构成对顶角吗？
∠2与∠4同样为对顶角
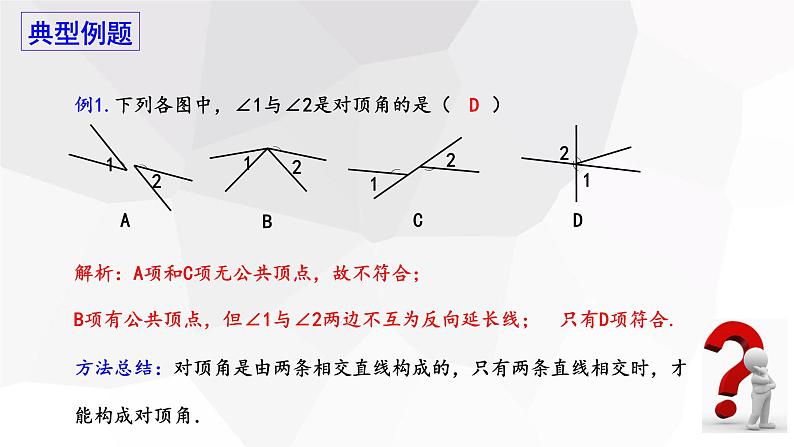
例1.下列各图中，∠1与∠2是对顶角的是（ ）
方法总结：对顶角是由两条相交直线构成的，只有两条直线相交时，才能构成对顶角．
解析：A项和C项无公共顶点，故不符合；
B项有公共顶点，但∠1与∠2两边不互为反向延长线；
辨认对顶角的要领： 一看是不是两条直线相交所成的角，对顶角与相交线是唇齿相依，哪里有相交直线，哪里就有对顶角，反过来，哪里有对顶角，哪里就有相交线； 二看是不是有公共顶点； 三看是不是没有公共边，符合这三个条件时，才能确定这两个角是对顶角，只具备一个或两个条件都不行.
上图(1)、(2)、(4)中∠1和∠2不是对顶角，(3)中∠1和∠2是对顶角.
2.说出下图中所有的对顶角.
解：由对顶角的定义可知，图中对顶角有：
∠FAQ和∠BAC、∠FAC和∠BAQ，
∠DBO和∠CBA、∠DBA和∠CB0，
∠PCE和∠BCA、∠PCA和∠BCE.
思考：∠1和∠3的大小有什么关系？你能说明吗？
∠1与∠2构成一个平角，
所以∠1+∠2=180°，
同样也可知∠3+∠2=180°，
那么就得到∠1=∠3.
于是我们得到对顶角的性质：对顶角相等.
例2.如图，直线AB、CD相交于点O，∠BOD与∠BOE互为余角，∠BOE=18°，求∠AOC的度数.
分析：根据余角定义可得∠BOD=90°-18°=72°，再根据对顶角相等可得∠AOC=∠BOD=72°.
解：因为∠BOD与∠BOE互为余角，
所以∠BOD+∠EOB=90°，
所以∠BOD=90°-18°=72°；
因为∠BOD=72°，直线AB、CD相交于点O，
所以∠AOC和∠BOD为对顶角，
所以∠AOC=∠BOD=72°(对顶角相等).
3.如图，已知∠1+∠2=100°，求∠3的度数．
解：因为∠1+∠2=100°，∠1=∠2（对顶角相等），
所以∠3=180°-50°=130°．
所以∠1=100°÷2=50°，
4.如图，已知直线AB、CD交于点O，且∠1：∠2=2：3，∠AOC=60°，求∠2的度数．
解：设∠1=2x，∠2=3x，
所以2x+3x=60°，x=12°，
则∠2=3x=3×12°=36°．
因为∠1：∠2=2：3，
所以∠AOC=60°=∠1+∠2，
因为∠AOC和∠DOB是对顶角(对顶角的定义)