



还剩8页未读,
继续阅读
初中数学北师大版八年级下册3 中心对称教课ppt课件
展开
这是一份初中数学北师大版八年级下册3 中心对称教课ppt课件,共15页。PPT课件主要包含了学习目标,新课导入,回顾与思考,概念剖析,完全重合,一中心对称的概念,AOA1O,中心对称的性质,典型例题,归纳总结等内容,欢迎下载使用。
1.理解中心对称及中心对称图形的概念和性质2.会根据中心对称的性质画成中心对称的图形
1.你还记得什么是轴对称图形吗?
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
2.下面扑克牌的牌面有什么特点?
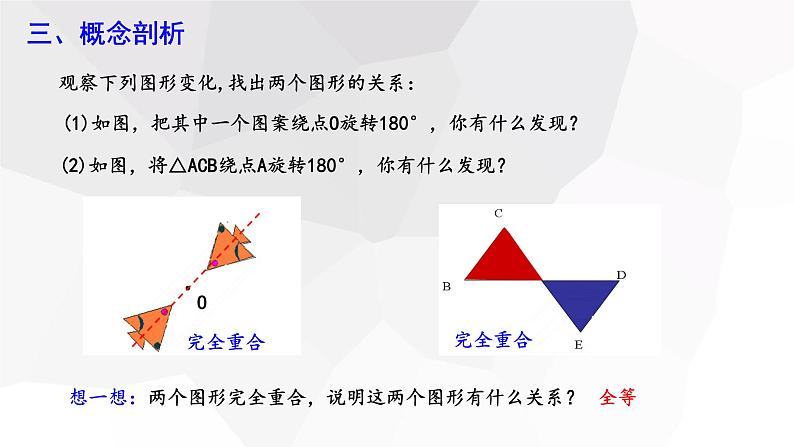
(1)如图,把其中一个图案绕点O旋转180°,你有什么发现?
(2)如图,将△ACB绕点A旋转180°,你有什么发现?
观察下列图形变化,找出两个图形的关系:
想一想:两个图形完全重合,说明这两个图形有什么关系?
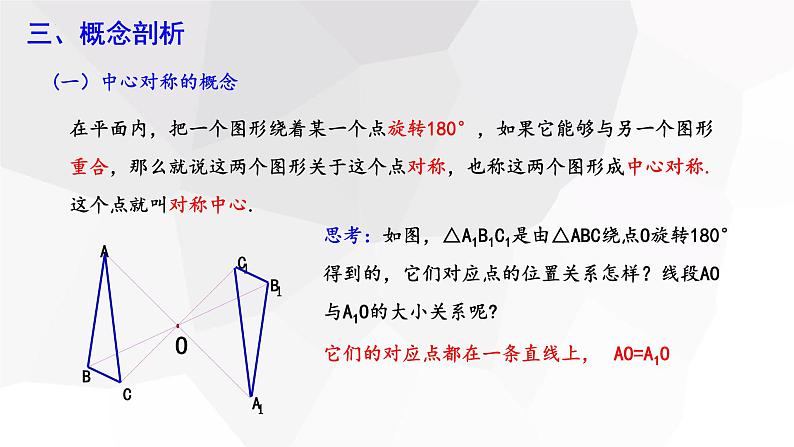
在平面内,把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称,也称这两个图形成中心对称.这个点就叫对称中心.
思考:如图,△A1B1C1是由△ABC绕点O旋转180°得到的,它们对应点的位置关系怎样?线段AO与A1O的大小关系呢?
它们的对应点都在一条直线上,
2.成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
1.关于中心对称的两个图形是全等形.
(二)中心对称图形的概念
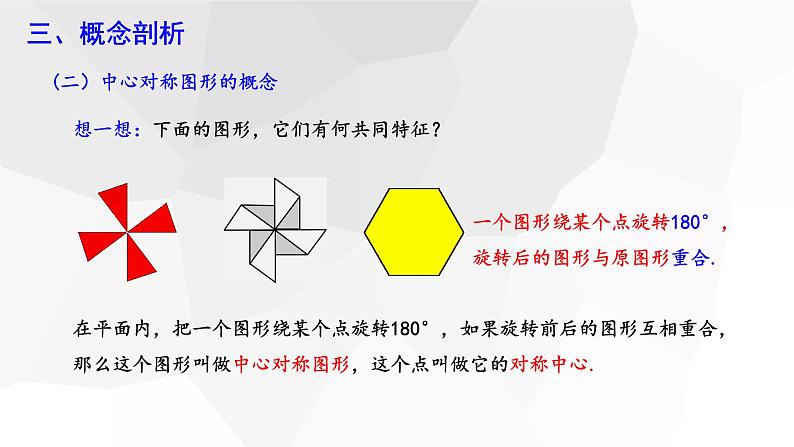
在平面内,把一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
想一想:下面的图形,它们有何共同特征?
一个图形绕某个点旋转180°,旋转后的图形与原图形重合.
讨论:中心对称与中心对称图形有什么区别和联系?
区别:中心对称指两个全等图形的相互位置关系, 中心对称图形指一个图形本身成中心对称.
联系:如果将中心对称图形的两个图形看成一个整体, 则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图形, 则它们成中心对称.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
例1:下面26个英文大写正体字母中,哪些是轴对称图形,哪些是中心对称图形?
解:26个大写英文字母中,是轴对称图形的有:A、B、C、D、E、H、I、K、M、O、T、U、V、W、X、Y,是中心对称图形的有:H、I、N、O、S、X、Z.
中心对称图形与轴对称图形有什么区别和联系?
轴对称图形与中心对称图形的区别和联系:
1.下图中的中心对称图形有 ,是轴对称图形的有 .
例2.(1)如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O.
分析:根据成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分,且被对称中心平分即可确定对称中心O.
提示:找出BB’的中点O,则点O即为所求.
解:根据观察,B、B’及C、C’应是两组对应点,连接BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)
思考:还有其他方法找出对称中心O吗?
(2)已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称(要求写出作法).
3.顺次连接A´、B´、C´、D´各点,
四边形A´B´C´D´就是所求的四边形
2.同样画B、C、D的对称点B´、C´、D´
1.连接AO 并延长到A´,使OA=OA´, 得到点A的对称点A´ .
方法总结:作图时需要结合中心对称的性质,作图的关键是先确定对称中心.
2.画一个与已知四边形ABCD中心对称的图形.(1)以顶点A为对称中心;(2)以BC边的中点为对称中心.
1.理解中心对称及中心对称图形的概念和性质2.会根据中心对称的性质画成中心对称的图形
1.你还记得什么是轴对称图形吗?
如果一个平面图形沿一条直线折叠后,直线两旁的部分能够互相重合,那么这个图形叫做轴对称图形,这条直线叫做对称轴.
2.下面扑克牌的牌面有什么特点?
(1)如图,把其中一个图案绕点O旋转180°,你有什么发现?
(2)如图,将△ACB绕点A旋转180°,你有什么发现?
观察下列图形变化,找出两个图形的关系:
想一想:两个图形完全重合,说明这两个图形有什么关系?
在平面内,把一个图形绕着某一个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称,也称这两个图形成中心对称.这个点就叫对称中心.
思考:如图,△A1B1C1是由△ABC绕点O旋转180°得到的,它们对应点的位置关系怎样?线段AO与A1O的大小关系呢?
它们的对应点都在一条直线上,
2.成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.
1.关于中心对称的两个图形是全等形.
(二)中心对称图形的概念
在平面内,把一个图形绕某个点旋转180°,如果旋转前后的图形互相重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心.
想一想:下面的图形,它们有何共同特征?
一个图形绕某个点旋转180°,旋转后的图形与原图形重合.
讨论:中心对称与中心对称图形有什么区别和联系?
区别:中心对称指两个全等图形的相互位置关系, 中心对称图形指一个图形本身成中心对称.
联系:如果将中心对称图形的两个图形看成一个整体, 则它们是中心对称图形.
如果将中心对称图形对称的部分看成两个图形, 则它们成中心对称.
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
例1:下面26个英文大写正体字母中,哪些是轴对称图形,哪些是中心对称图形?
解:26个大写英文字母中,是轴对称图形的有:A、B、C、D、E、H、I、K、M、O、T、U、V、W、X、Y,是中心对称图形的有:H、I、N、O、S、X、Z.
中心对称图形与轴对称图形有什么区别和联系?
轴对称图形与中心对称图形的区别和联系:
1.下图中的中心对称图形有 ,是轴对称图形的有 .
例2.(1)如图,已知△ABC与△A’B’C’中心对称,求出它们的对称中心O.
分析:根据成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分,且被对称中心平分即可确定对称中心O.
提示:找出BB’的中点O,则点O即为所求.
解:根据观察,B、B’及C、C’应是两组对应点,连接BB’、CC’,BB’、CC’相交于点O,则点O即为所求(如图)
思考:还有其他方法找出对称中心O吗?
(2)已知四边形ABCD和点O,画四边形A′B′C′D′,使它与已知四边形关于这一点对称(要求写出作法).
3.顺次连接A´、B´、C´、D´各点,
四边形A´B´C´D´就是所求的四边形
2.同样画B、C、D的对称点B´、C´、D´
1.连接AO 并延长到A´,使OA=OA´, 得到点A的对称点A´ .
方法总结:作图时需要结合中心对称的性质,作图的关键是先确定对称中心.
2.画一个与已知四边形ABCD中心对称的图形.(1)以顶点A为对称中心;(2)以BC边的中点为对称中心.













