



初中数学沪科版九年级下册24.6.1 正多边形与圆集体备课课件ppt
展开1.了解正多边形的概念.2.了解正多边形与圆的关系3.能用尺规作图:作圆的内接正方形和内接正六边形.
看下面这些美丽的图案,都是在日常生活中经常能看到的.你能从这些图案中找出哪些正多边形?
问题1 什么叫做正多边形?
各边相等,各角也相等的多边形叫做正多边形.
问题2 正多边形是轴对称图形吗?是中心对称图形吗?
正多边形是轴对称图形;当边数为偶数时,正多边形也是中心对称图形.
圆既是轴对称图形又是旋转对称图形.
各边相等、各角也相等的多边形叫做正多边形.
正多边形与圆有非常密切的关系,把一个圆分成n条相等的弧,就可以作出这个圆的内接或外切正n边形.
接下来,我们就一起以圆内接正五边形为例证明.
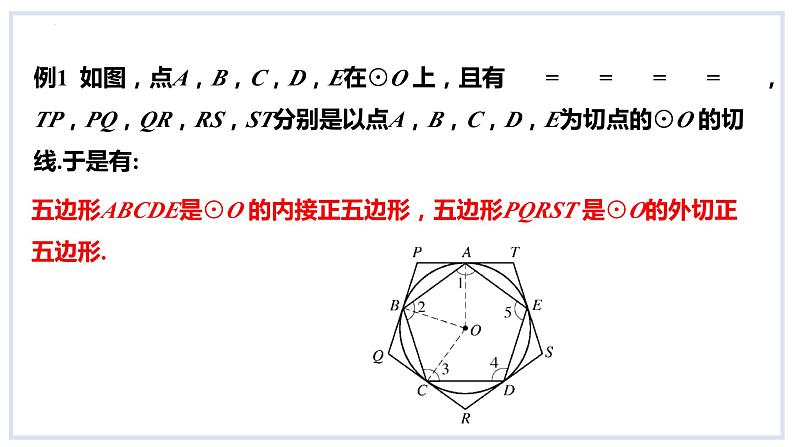
五边形ABCDE是⊙O 的内接正五边形,五边形PQRST 是⊙O的外切正五边形.
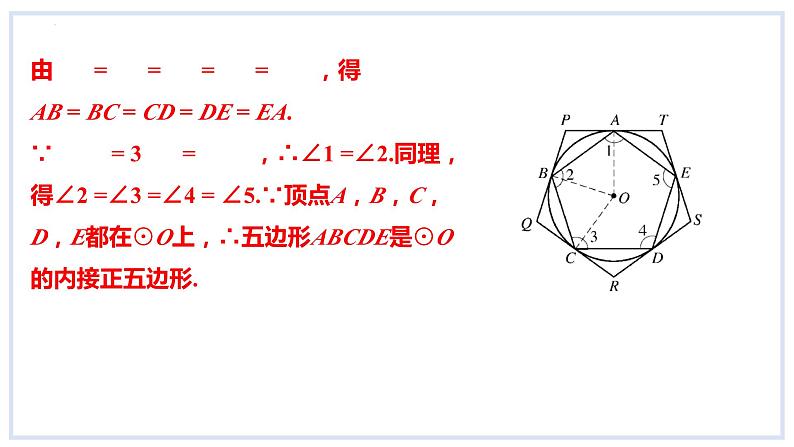
由 = = = = ,得AB = BC = CD = DE = EA.∵ = 3 = ,∴∠1 =∠2.同理,得∠2 =∠3 =∠4 = ∠5.∵顶点A,B,C,D,E都在⊙O上,∴五边形ABCDE是⊙О的内接正五边形.
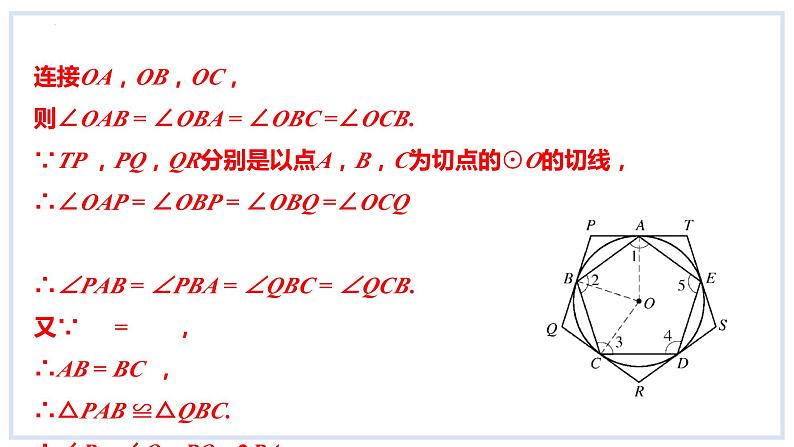
连接OA,OB,OC,则∠OAB = ∠OBA = ∠OBC =∠OCB.∵TP ,PQ,QR分别是以点A,B,C为切点的⊙O的切线,∴∠OAP = ∠OBP = ∠OBQ =∠OCQ ∴∠PAB = ∠PBA = ∠QBC = ∠QCB.又∵ = ,∴AB = BC ,∴△PAB ≌△QBC.∴∠P = ∠Q,PQ = 2PA.
同理,得∠Q = ∠R = ∠S = ∠T,QR = RS = ST = TP = 2PA.∵五边形PQRST的各边都与⊙O 相切,∴五边形PQRST是⊙O的外切正五边形.
由上可知,通过等分圆周的方法能作出正多边形.
如图,其他正多边形也有类似的结论.
任何正多边形都有一个外接圆和一个内切圆.
(1)用量角器等分圆周
①正四边形的作法如图(1),用直尺和圆规作⊙O的两条互相垂直的直径,就可以把⊙O分成4等份,从而作出正四边形.
对于一些特殊的正n边形,还可以用直尺和圆规来等分圆周.
我们再逐次平分各边所对的弧,就可以作出正八边形[图(2)]、正十六边形等.
②正六边形的作法如图(1) ,设⊙O的半径为R,通常先作出⊙O的一条直径AB ,然后分别以点A,B为圆心、R为半径作弧,与⊙O交于点C,D,E,F,从而得到⊙O的6等份点,作出正六边形.
如果再逐次等分各边所对的弧,就可作出正十二边形、正二十四边形等.
我们可以连接6等份圆周的相间两个点,得到正三角形,如图(2).
1. 如图,AD为⊙O的直径,作⊙O的内接正三角形ABC,甲、乙两人的作法分别如下:
甲:(1)以D为圆心,OD长为半径画圆弧,交⊙O于B,C两点; (2)连接AB,BC,AC.△ABC即为所求作的三角形.
乙:(1)作OD的中垂线,交⊙O于B,C两点; (2)连接AB,AC.△ABC即为所求作的三角形.
对于甲、乙两人的作法,可判断( )A.甲对,乙不对 B.甲不对,乙对C.两人都对 D.两人都不对
2.利用尺规作一个已知圆的内接正方形.
作法:(1)用直尺任作⊙O的一条直径AC;(2)作与直径AC垂直的直径BD;(3)顺次连接所得的圆上四点,则四边形ABCD即为所求作的正方形.
初中数学24.6.2 正多边形的性质图文ppt课件: 这是一份初中数学<a href="/sx/tb_c102908_t3/?tag_id=26" target="_blank">24.6.2 正多边形的性质图文ppt课件</a>,共22页。PPT课件主要包含了中心角,边心距等内容,欢迎下载使用。
初中数学沪科版九年级下册24.6.1 正多边形与圆作业课件ppt: 这是一份初中数学沪科版九年级下册24.6.1 正多边形与圆作业课件ppt,共11页。
初中数学沪科版九年级下册24.6.1 正多边形与圆教学演示课件ppt: 这是一份初中数学沪科版九年级下册24.6.1 正多边形与圆教学演示课件ppt,共23页。PPT课件主要包含了图片引入,观察与思考,知识要点,正多边形,各边相等,各角相等,缺一不可,练一练,典例精析,正多边形与圆的关系等内容,欢迎下载使用。













