沪科版九年级下册24.4.3 切线长定理备课课件ppt

这是一份沪科版九年级下册24.4.3 切线长定理备课课件ppt，共19页。PPT课件主要包含了一切线长定理，连接OP，PAPB，∠OPA∠OPB，几何语言，拓展延伸等内容，欢迎下载使用。
1. 能用尺规作图：过圆外一点作圆的切线；2. 探索并证明切线长定理：过圆外一点的两条切线长相等.
前面我们已经学习了切线的判定定理和性质定理，已知⊙O和⊙O外一点P，你能够过点P画出⊙O的切线吗？
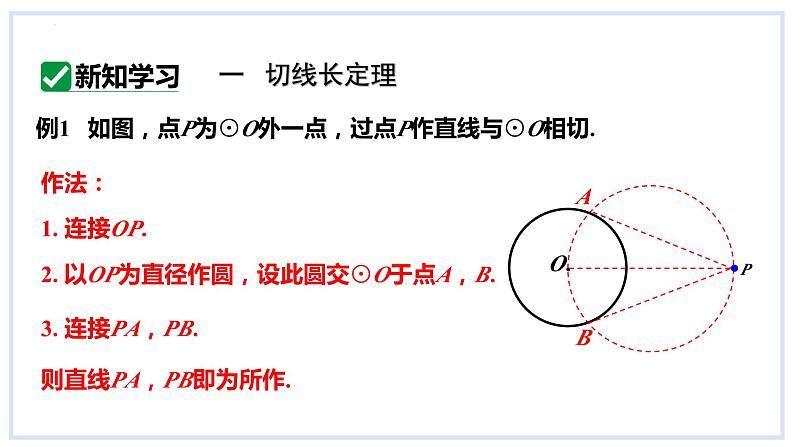
例1 如图，点Р为⊙O外一点，过点Р作直线与⊙O相切.
则直线PA，PB即为所作.
2. 以OP为直径作圆，设此圆交⊙O于点A，B.
3. 连接PA，PB.
过圆外一点能够作圆的两条切线.切线上一点到切点之间的线段长叫做这点到圆的切线长.
如图，PA，PB为⊙O的两条切线，点A、B为切点. 线段PA、PB的长就是点P到⊙O的切线长.
注意：切线是直线，不可度量；切线长是切线上一点与切点之间的线段的长，可以度量.
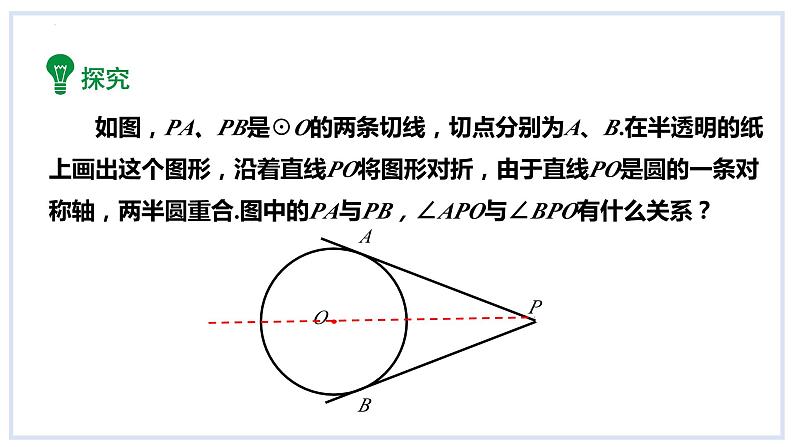
如图，PA、PB是☉O的两条切线，切点分别为A、B.在半透明的纸上画出这个图形，沿着直线PO将图形对折，由于直线PO是圆的一条对称轴，两半圆重合.图中的PA与PB，∠APO与∠BPO有什么关系？
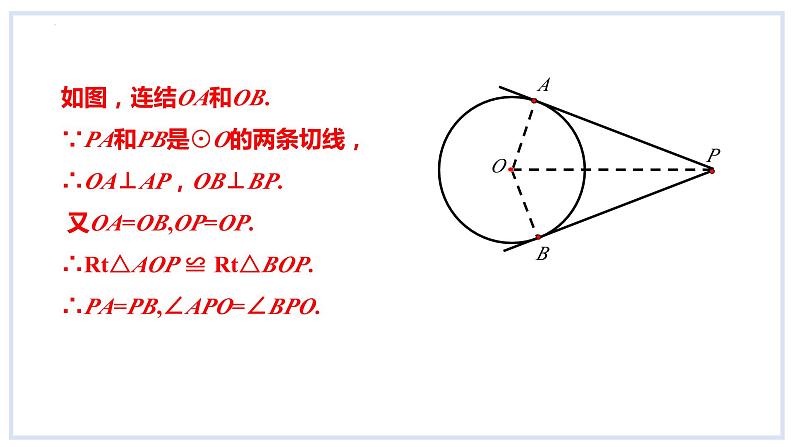
如图，连结OA和OB.∵PA和PB是⊙O的两条切线，∴OA⊥AP，OB⊥BP. 又OA=OB,OP=OP.∴Rt△AOP ≌ Rt△BOP.∴PA=PB,∠APO=∠BPO.
*切线长定理 过圆外一点作圆的两条切线，两条切线长相等，圆心与这一点的连线平分两条切线的夹角.
PA、PB分别切☉O于点A、B
例1 已知:如图，四边形ABCD的边AB，BC，CD，DA 和⊙O分别相切于点E，F，G，H.求证:AB + CD = DA +BC.
例2 为了测量一个圆形铁环的半径，某同学采用了如下办法：将铁环平放在水平桌面上，用一个锐角为30°的三角板和一个刻度尺，按如图所示的方法得到相关数据，进而可求得铁环的半径，若三角板与圆相切且测得PA=5cm，求铁环的半径．
分析：欲求半径，取圆的圆心为O，连OA，OP，由切线性质知△OPA为直角三角形，从而在Rt△OPA中由勾股定理易求得半径．
解：如图，设铁环的圆心为O，过O作OQ⊥AB于Q，连接OP、OA.
∵AP、AQ为⊙O的切线，∴AO为∠PAQ的平分线，即∠PAO＝∠QAO.
又∠BAC＝60°，∠PAO＋∠QAO＋∠BAC＝180°，∴∠PAO＝∠QAO＝60°.
若连结两切点A、B，AB交OP于点M.你又能得出什么新的结论？请给出证明.
结论：OP垂直平分AB.证明：∵PA，PB是⊙O的切线，点A，B是切点 ∴PA = PB ，∠OPA=∠OPB ∴△PAB是等腰三角形，PM为顶角的平分线 ∴OP垂直平分AB.
若延长PO交⊙O于点C，连接CA、CB，你又能得出什么新的结论？请给出证明.
1.下列说法正确的是(　　)A．过任意一点总可以作圆的两条切线B．圆的切线长就是圆的切线的长度C．过圆外一点所画的圆的两条切线长相等D．过圆外一点所画的圆的切线长一定大于圆的半径
2. 如图，AB、AC、BD是☉O的切线，P、C、D为切点，如果AB= 5，AC=3，则BD = .
1.如图，四边形ABCD为⊙O的内接四边形，过点A，B的切线PM，PN交圆外于点P，若∠C＝135°，∠MAD＝60°，则∠P的度数为_____．
2. 如图，△ABC三边都与⊙O 相切，求证：AB + CF = AC + BF.
证明：∵△ABC三边都与⊙O 相切，∴AD=AE ①，BD=BF ②，CF=CE ③，∴①+②+③得，AD+BD+CF=AE+BF+CE，∴AB+CF=AC+BF.
3.如图，AB是⊙O的直径，C为⊙O外一点，CA，CD分别切⊙O于点A，D，连接BD，AD，若∠C＝50°，求∠DBA的大小．
解：∵CA，CD是⊙O的切线， ∴CA = CD，∵∠C = 50°， ∴∠CAD = ∠CDA = 65°，∵CA⊥AB，AB是⊙O的直径， ∴∠ADB = ∠CAB = 90°，∴∠DBA＋∠DAB = 90°，∠CAD＋∠DAB = 90°，∴∠DBA = ∠CAD = 65°.