初中数学沪科版九年级下册24.4.2 切线的判定与性质教案配套ppt课件

这是一份初中数学沪科版九年级下册24.4.2 切线的判定与性质教案配套ppt课件，共20页。PPT课件主要包含了没有公共点，个公共点，d5cm，二切线的性质定理，于是可得，应用格式，解得m≤2，又∵⊙O的半径为2等内容，欢迎下载使用。

1.了解直线与圆的位置关系.2.掌握切线的概念.3.会运用直线与圆的位置关系进行有关计算．4.理解并掌握圆的切线的性质定理.5.能运用圆的切线的性质定理解决问题.
如果我们把太阳看成一个圆，地平线看成一条直线，那你能根据直线和圆的公共点个数想象一下，直线与圆有几种位置关系吗？
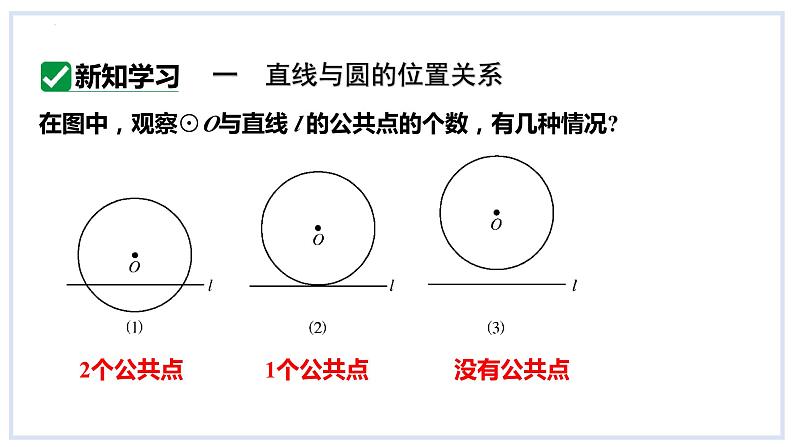
在图中，观察⊙O与直线 l 的公共点的个数，有几种情况?
一 直线与圆的位置关系
可以发现，直线与圆有三种位置关系：
直线与圆没有公共点，这时直线与圆的位置关系叫做相离
直线与圆只有一个公共点，这时直线与圆的位置关系叫做相切. 这条直线叫做圆的切线，这个公共点叫做切点.
直线与圆有两个公共点，这时直线与圆的位置关系叫做相交，这条直线叫做圆的割线.
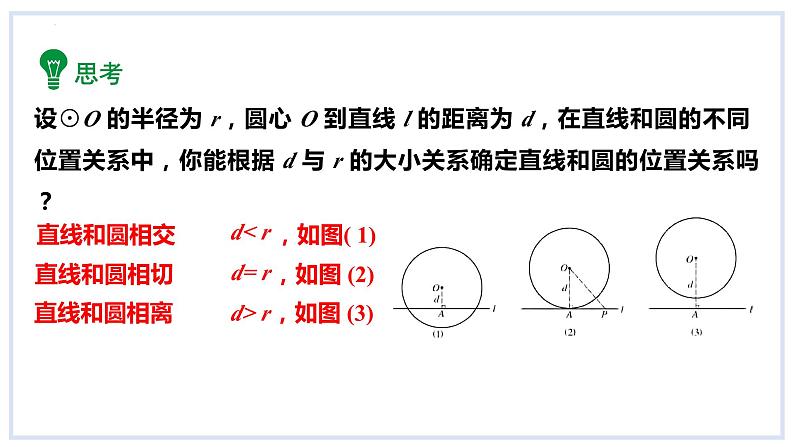
设⊙O 的半径为 r，圆心 O 到直线 l 的距离为 d，在直线和圆的不同位置关系中，你能根据 d 与 r 的大小关系确定直线和圆的位置关系吗？
判定直线与圆的位置关系的方法有2种：1.由直线与圆的公共点的个数来判断;2.由圆心到直线的距离 d 与半径 r 大小关系来判断.
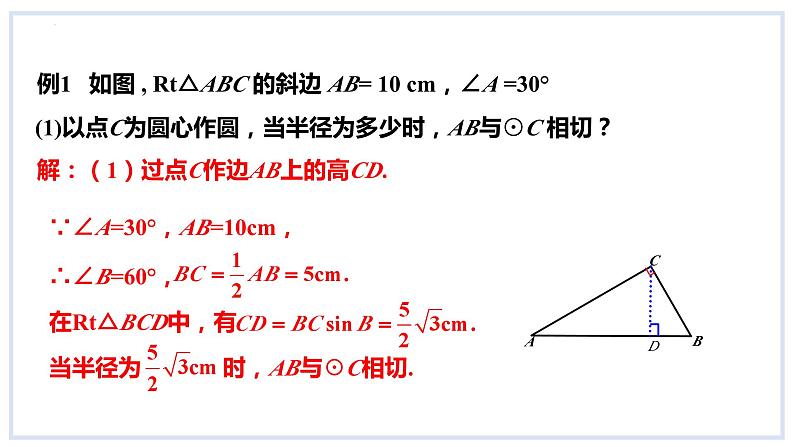
(1)以点C为圆心作圆，当半径为多少时，AB与⊙C 相切？
例1 如图 , Rt△ABC 的斜边 AB= 10 cm，∠A =30°
解：（1）过点C作边AB上的高CD.
(2)以点C为圆心、半径r分别为4 cm和5 cm作两个圆，这两个圆与斜边AB分别有怎样的位置关系？
0 cm ≤ d < 5 cm
直线 l 与圆O相切于点A时，OA与 l 有什么位置关系？
当直线l与⊙O相切时，切点为A，连接OA.这时，如在直线l上任取一个不同于点A的点Р，连接OP，因为点Р在⊙O外，所以OP >OA.这就是说，OA是点О到直线l上任一点的连线中最短的，故OA⊥l.
切线性质 圆的切线垂直于经过切点的半径.
∵直线l 是⊙O 的切线，A是切点，∴直线l ⊥OA.
例2 如图，PA为⊙O的切线，A为切点．直线PO与⊙O交于 B、C 两点，∠P＝30°，连接AO、AB、AC.求证：△ACB≌△APO；
在△ACB和△APO中，∠BAC＝∠OAP，AB＝AO，∠ABO＝∠AOB，∴△ACB≌△APO.
又∵BC为⊙O的直径，∴∠BAC＝90°.
1. 如图，在 ⊙O 中，AB 为直径，BC 为弦，CD 为切线，连接 OC. 若∠BCD = 50°，则∠AOC 的度数为(　　)A. 40° B. 50° C. 80° D. 100°
2. 如图，⊙O 切 PB 于点 B，PB = 4，PA = 2，则 ⊙O 的半径是多少？
解：连接 OB，易知∠OBP = 90°.
1. 如图，AB 为⊙O 的直径，D 为 AB 延长线上一点，DC 与⊙O 相切于点 C，∠DAC = 30°. 若⊙O 的半径长 1 cm，则 CD = cm.
2. 如图，在☉O 的内接四边形 ABCD 中，AB 是直径，∠BCD = 120°，过 D 点的切线 PD 与直线 AB 交于点 P，则∠ADP 的度数为( ) A．40° B．35° C．30° D．45°
∴直线与圆相切或相交．
即8－4×2×（m－1）≥0.