浙江省温州市苍南县2023—-2024学年上学期七年级期末数学试卷

这是一份浙江省温州市苍南县2023—-2024学年上学期七年级期末数学试卷，共16页。试卷主要包含了填空题，解答题等内容，欢迎下载使用。
1．（3分）在，0，，3.14四个数中，属于无理数的是
A．B．0C．D．3.14
2．（3分）杭州市2011年元旦的最高气温为，最低气温为，这天的最高气温比最低气温高
A．B．C．D．
3．（3分）的立方根是
A．2B．C．D．
4．（3分）2023年杭州亚运会恰逢中秋节和国庆节，“双节”叠加带来了巨大的人流量，10月1日当天的观赛人数达到290000人，数290000用科学记数法表示为
A．B．C．D．
5．（3分）如图，一骑马少年从M地出发，经过小溪l回到位于N地的家中，为使路程最短，则过小溪l的地方应选择（ ）
A．A地B．B地C．C地D．D地
6．（3分）苍南因地处玉苍山之南，故取县名为苍南．其总面积为1079.34平方公里，数1079.34精确到个位，则近似值为
A．1080B．1079.3C．1079D．1070
7．（3分）已知，根据等式的基本性质，下列变形错误的是
A．B．C．D．
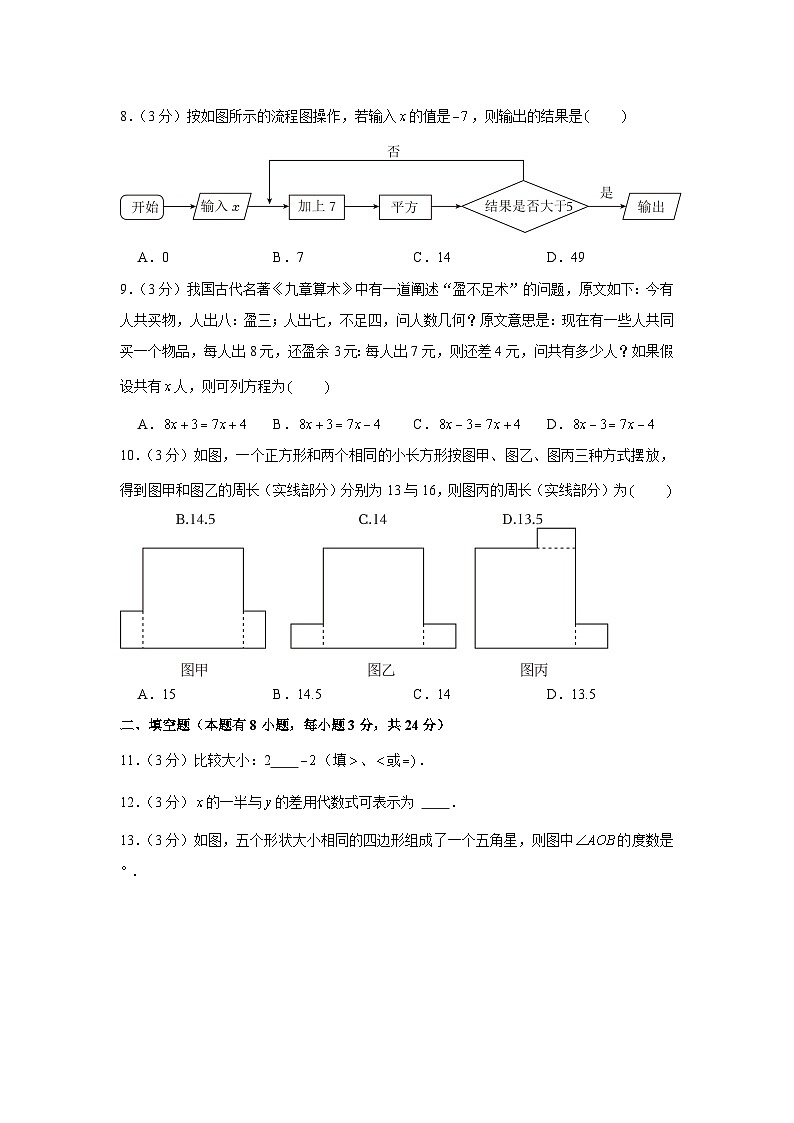
8．（3分）按如图所示的流程图操作，若输入的值是，则输出的结果是
A．0B．7C．14D．49
9．（3分）我国古代名著《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八：盈三；人出七，不足四，问人数几何？原文意思是：现在有一些人共同买一个物品，每人出8元，还盈余3元：每人出7元，则还差4元，问共有多少人？如果假设共有人，则可列方程为
A．B．C．D．
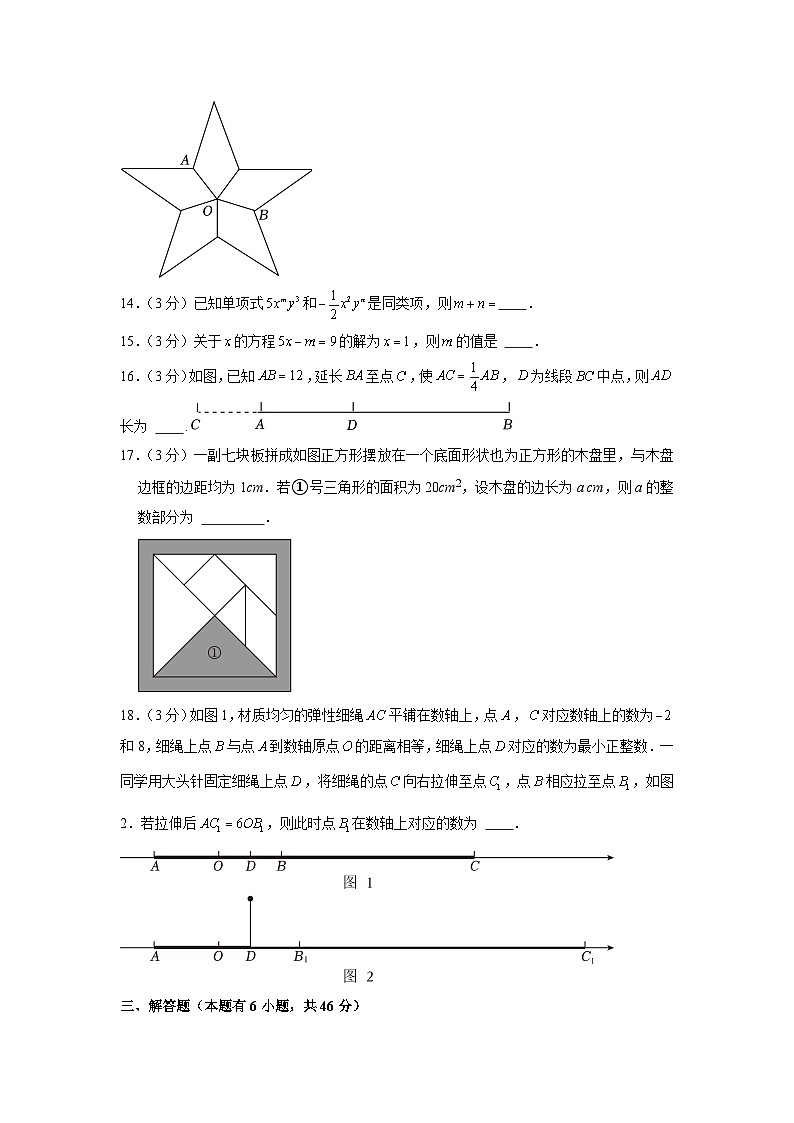
10．（3分）如图，一个正方形和两个相同的小长方形按图甲、图乙、图丙三种方式摆放，得到图甲和图乙的周长（实线部分）分别为13与16，则图丙的周长（实线部分）为
A．15B．14.5C．14D．13.5
二、填空题（本题有8小题，每小题3分，共24分）
11．（3分）比较大小：2 （填、或．
12．（3分）的一半与的差用代数式可表示为 ．
13．（3分）如图，五个形状大小相同的四边形组成了一个五角星，则图中的度数是 ．
14．（3分）已知单项式和是同类项，则 ．
15．（3分）关于的方程的解为，则的值是 ．
16．（3分）如图，已知，延长至点，使，为线段中点，则长为
17．（3分）一副七块板拼成如图正方形摆放在一个底面形状也为正方形的木盘里，与木盘边框的边距均为1cm．若①号三角形的面积为20cm2，设木盘的边长为a cm，则a的整数部分为 ．
18．（3分）如图1，材质均匀的弹性细绳平铺在数轴上，点，对应数轴上的数为和8，细绳上点与点到数轴原点的距离相等，细绳上点对应的数为最小正整数．一同学用大头针固定细绳上点，将细绳的点向右拉伸至点，点相应拉至点，如图2．若拉伸后，则此时点在数轴上对应的数为 ．
三、解答题（本题有6小题，共46分）
19．（6分）计算：
（1）；
（2）．
20．（8分）解方程：
（1）；
（2）．
21．（6分）先化简，再求值：，其中，
22．（8分）【素材】图1为某景区游览图，相邻两地标之间的路程如图所示．
【问题1】小明以游客中心为原点O，游客中心往碗窑博物馆方向为正方向，碗窑大桥对应数轴上点A，画出数轴，如图2．请你在数轴上标出B吊脚楼、C倒焰窑、D碗窑博物馆的位置．
【问题2】小李以50米/分钟的速度从碗窑博物馆往游客中心出发，过景点均不停留．小王同时以相同的速度从游客中心出发往碗窑博物馆方向游览，经过每一景点均停留8分钟．请问他们经过多长时间相遇？并把相遇地点E标在问题1的数轴上．（注：请画在答题纸上）
23．（8分）如图，直线与直线交于点，射线在 内部，是的平分线，且．
（1）若，求的度数．
（2）若，求的度数．
24．（10分）对联是中华传统文化的瑰宝．如图1所示，对联装裱后，上、下空白处分别称为天头和地头，左、右空白处统称为边．一般情况下，天头长与地头长的比是6：4，左、右边的边宽相等，且为天头长与地头长的和的，设左、右边的边宽为x cm．
（1）用含x的代数式分别表示天头长和地头长．
（2）现要装裱一副五言联，该五言联的长为92cm，宽为25cm，如图2所示，装裱五言联用的卷轴的长是宽的4倍．求五言联装裱预留的天头长．
（3）如图3，徐老师裁出两张长方形纸张准备写一副七言联，每张正好划出7个正方形方格，正方形方格的边长为a cm．若装裱用的卷轴长为190cm，正方形方格的边长比装裱后的边宽大，且两者长度均为整数，求徐老师裁剪的长方形纸张的长．
2023-2024学年浙江省温州市苍南县七年级（上）期末数学试卷
参考答案与试题解析
一、选择题（本题有10小题，每小题3分，共30分.每小题只有一个选项是正确的，不选、多选、
1．（3分）在，0，，3.14四个数中，属于无理数的是
A．B．0C．D．3.14
【解答】解：．属于无理数，故本选项符合题意；
．0是整数，属于有理数，故本选项不符合题意；
．是分数，属于有理数，故本选项不符合题意；
．3.14是有限小数，属于有理数，故本选项不符合题意．
故选：．
2．（3分）杭州市2011年元旦的最高气温为，最低气温为，这天的最高气温比最低气温高
A．B．C．D．
【解答】解：，
，
．
故选：．
3．（3分）的立方根是
A．2B．C．D．
【解答】解：，
的立方根是．
故选：．
4．（3分）2023年杭州亚运会恰逢中秋节和国庆节，“双节”叠加带来了巨大的人流量，10月1日当天的观赛人数达到290000人，数290000用科学记数法表示为
A．B．C．D．
【解答】解：，
故选：．
5．（3分）如图，一骑马少年从M地出发，经过小溪l回到位于N地的家中，为使路程最短，则过小溪l的地方应选择（ ）
A．A地B．B地C．C地D．D地
【解答】解：依据两点之间，线段最短，可知为使路程最短，则过小溪l的地方应选择C地．
故选：C．
6．（3分）苍南因地处玉苍山之南，故取县名为苍南．其总面积为1079.34平方公里，数1079.34精确到个位，则近似值为
A．1080B．1079.3C．1079D．1070
【解答】解：把1079.34精确到个位得到的近似数是1079．
故选：．
7．（3分）已知，根据等式的基本性质，下列变形错误的是
A．B．C．D．
【解答】解：将等式的两边同时加上1，得：，
故选项正确，不符合题意；
将等式的两边同时减去1，得：，
故选项正确，不符合题意；
将等式的两边同时乘以，得：，
故选项不正确，符合题意；
将等式的两边同时除以2，得：，
故选项正确，不符合题意．
故选：．
8．（3分）按如图所示的流程图操作，若输入的值是，则输出的结果是
A．0B．7C．14D．49
【解答】解：输入的的值是，
则，返回继续运算；
，输出结果；
故选：．
9．（3分）我国古代名著《九章算术》中有一道阐述“盈不足术”的问题，原文如下：今有人共买物，人出八：盈三；人出七，不足四，问人数几何？原文意思是：现在有一些人共同买一个物品，每人出8元，还盈余3元：每人出7元，则还差4元，问共有多少人？如果假设共有人，则可列方程为
A．B．C．D．
【解答】解：根据题意得．
故选：．
10．（3分）如图，一个正方形和两个相同的小长方形按图甲、图乙、图丙三种方式摆放，得到图甲和图乙的周长（实线部分）分别为13与16，则图丙的周长（实线部分）为
A．15B．14.5C．14D．13.5
【解答】解：设正方形的边长为，小长方形的长为，宽为，
则图甲的周长可表示为：，
所以①；
图乙的周长可表示为：，
所以②；
图丙的周长可表示为：．
将①②两式相加再除以2得，
，
即，
所以图丙的周长为14.5．
故选：．
二、填空题（本题有8小题，每小题3分，共24分）
11．（3分）比较大小：2 （填、或．
【解答】解：根据有理数比较大小的方法，可得
．
故答案为：．
12．（3分）的一半与的差用代数式可表示为 ．
【解答】解：根据题意可知．
故答案为：．
13．（3分）如图，五个形状大小相同的四边形组成了一个五角星，则图中的度数是 144 ．
【解答】解：由题意可得，
故答案为：144．
14．（3分）已知单项式和是同类项，则 5 ．
【解答】解：单项式和是同类项，
，，
，
故答案为：5．
15．（3分）关于的方程的解为，则的值是 ．
【解答】解：把代入方程得：，
解得：，
故答案为：．
16．（3分）如图，已知，延长至点，使，为线段中点，则长为 4.5
【解答】解：，，
，
，
为线段的中点，
，
．
故答案为：4.5．
17．（3分）一副七块板拼成如图正方形摆放在一个底面形状也为正方形的木盘里，与木盘边框的边距均为1cm．若①号三角形的面积为20cm2，设木盘的边长为a cm，则a的整数部分为 10 ．
【解答】解：如图，
由题意得①是等腰直角三角形，面积为20cm2，
∴，
即AC＝BC＝（cm），
∵∠ACB＝90°，
∴由勾股定理得（cm），
∴（cm），
即（cm），
∵，
即，
∴，
∴的整数部分为10，
即a的整数部分为10，
故答案为：10．
18．（3分）如图1，材质均匀的弹性细绳平铺在数轴上，点，对应数轴上的数为和8，细绳上点与点到数轴原点的距离相等，细绳上点对应的数为最小正整数．一同学用大头针固定细绳上点，将细绳的点向右拉伸至点，点相应拉至点，如图2．若拉伸后，则此时点在数轴上对应的数为 4 ．
【解答】解：如图1，，，，，，
如图2，设，，
根据，列方程：
．
．
．
故答案为：4．
三、解答题（本题有6小题，共46分）
19．（6分）计算：
（1）；
（2）．
【解答】解：（1）原式
；
（2）原式
．
20．（8分）解方程：
（1）；
（2）．
【解答】解：（1）原方程去括号得：，
移项，合并同类项得：，
系数化为1得：；
（2）原方程去分母得：，
移项，合并同类项得：．
21．（6分）先化简，再求值：，其中，
【解答】解：原式
；
当，时，
原式．
22．（8分）【素材】图1为某景区游览图，相邻两地标之间的路程如图所示．
【问题1】小明以游客中心为原点O，游客中心往碗窑博物馆方向为正方向，碗窑大桥对应数轴上点A，画出数轴，如图2．请你在数轴上标出B吊脚楼、C倒焰窑、D碗窑博物馆的位置．
【问题2】小李以50米/分钟的速度从碗窑博物馆往游客中心出发，过景点均不停留．小王同时以相同的速度从游客中心出发往碗窑博物馆方向游览，经过每一景点均停留8分钟．请问他们经过多长时间相遇？并把相遇地点E标在问题1的数轴上．（注：请画在答题纸上）
【解答】解：（1）∵游客中心为原点O，碗窑大桥为点A，
∴数轴上一个单位是100米，
由题得出各景点之间的距离，OB＝200米，BC＝400米，CD＝800米，
∴所标出B吊脚楼、C倒焰窑、D碗窑博物馆的位置如图所示，
（2）800+350＝1150，1150÷50＝23，
小李到达手工作坊时用时23分钟，
200+50＝250，250÷50＝5，5+16＝21，
小王到达手工作坊停留后用时21分钟，
∴相遇点应在倒焰窑和手工作坊之间，
设相遇时间为t分钟，
由题得，800+350﹣21×50＝100（t﹣21），
∴t＝22，
∴他们经过22分钟相遇，
相遇点如图所示点E．

23．（8分）如图，直线与直线交于点，射线在 内部，是的平分线，且．
（1）若，求的度数．
（2）若，求的度数．
【解答】解：（1），
，
，
，
是的平分线，
，
，
．
（2）设，则，
，
，
，
是的平分线，
，
，
，
，
．
24．（10分）对联是中华传统文化的瑰宝．如图1所示，对联装裱后，上、下空白处分别称为天头和地头，左、右空白处统称为边．一般情况下，天头长与地头长的比是6：4，左、右边的边宽相等，且为天头长与地头长的和的，设左、右边的边宽为x cm．
（1）用含x的代数式分别表示天头长和地头长．
（2）现要装裱一副五言联，该五言联的长为92cm，宽为25cm，如图2所示，装裱五言联用的卷轴的长是宽的4倍．求五言联装裱预留的天头长．
（3）如图3，徐老师裁出两张长方形纸张准备写一副七言联，每张正好划出7个正方形方格，正方形方格的边长为a cm．若装裱用的卷轴长为190cm，正方形方格的边长比装裱后的边宽大，且两者长度均为整数，求徐老师裁剪的长方形纸张的长．
【解答】解：（1）∵左、右边的边宽为x cm，且为天头长与地头长的和的，
∴天头长与地头长的和为10x cm，
∵天头长与地头长的比是6：4，
∴天头长为10x•＝6x（cm），地头长为10x•＝4x（cm）；
（2）根据题意，装裱五言联用的卷轴的长为（92+10x）cm，宽为（25+2x）cm，
∵卷轴的长是宽的4倍，
∴92+10x＝4（25+2x），
解得x＝4，
∴6x＝6×4＝24，
∴五言联装裱预留的天头长24cm；
（3）∵装裱用的卷轴长为190cm，
∴7a+10x＝190，
∴a＝，
∵a＞x，a与x都是正整数，
∴x＝5，a＝20；
∴7a＝7×20＝140，
∴徐老师裁剪的长方形纸张的长为140cm．