初中数学北师大版八年级下册2 直角三角形教学ppt课件

这是一份初中数学北师大版八年级下册2 直角三角形教学ppt课件，共30页。PPT课件主要包含了复习导入，探索研究，c2a2+b2，∴a2+b2c2，典例精练，课堂练习，课堂小结，布置作业等内容，欢迎下载使用。
(1)直角三角形的两个锐角互余；(2)勾股定理:直角三角形两直角边的平方和等于斜边的平方;(3)在直角三角形中,如果一个锐角等于30°，那么它所对的直角边等于斜边的一半.
提问：直角三角形有什么性质？
这节课我们一起来证明直角三角形的判定与性质.
问题：直角三角形的两锐角互余，为什么？
根据三角形的内角和定理，即可得到“直角三角形的两锐角互余”.
如果一个三角形中有两个锐角互余，那么这个三角形是直角三角形吗？
(一)直角三角形-角的性质
已知：如图，在△ABC中， ∠A +∠B=90°，证明：△ABC是直角三角形
在△ABC中，因为 ∠A +∠B+∠C=180°， 又∠A +∠B=90°，所以∠C=90°. 于是△ABC是直角三角形.
定理：有两个角互余的三角形是直角三角形
命题：有两个角互余的三角形是直角三角形
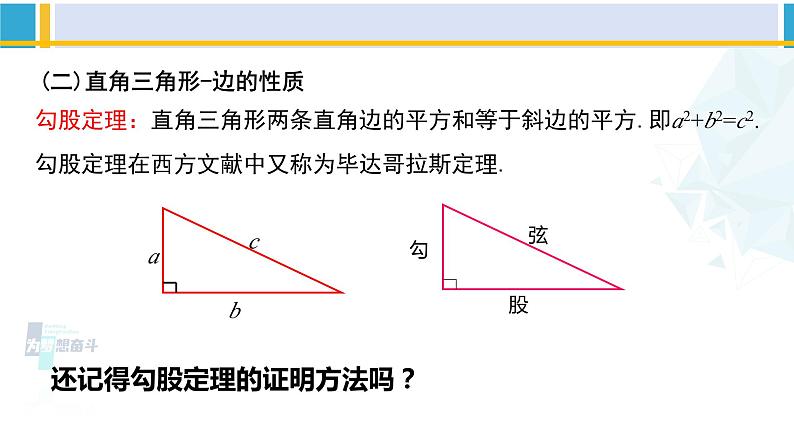
勾股定理：直角三角形两条直角边的平方和等于斜边的平方.即a2+b2=c2.勾股定理在西方文献中又称为毕达哥拉斯定理.
还记得勾股定理的证明方法吗？
(二)直角三角形-边的性质
(a+b)2 = c2 + 4× ab
a2+2ab+b2 = c2 +2ab
c2= 4 × ab +(b-a)2
c2 =2ab+b2-2ab+a2
勾股定理的证明—割补法
勾股定理的证明—总统证明法
美国第二十任总统伽菲尔德,在 1876年利用了梯形面积公式证明勾股定理.
伽菲尔德的证法在数学史上被传为佳话,后来，人们为了纪念他对勾股定理直观.简捷.易懂.明了的证明，就把这一证法称为“总统”证法 ．
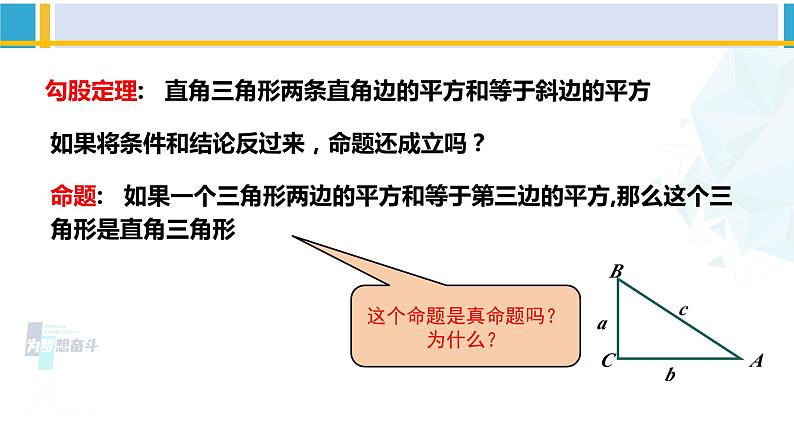
勾股定理: 直角三角形两条直角边的平方和等于斜边的平方
命题: 如果一个三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
如果将条件和结论反过来，命题还成立吗？
这个命题是真命题吗？为什么？
已知：如图，在△ABC中，AC2+BC2=AB2.求证：△ABC是直角三角形．
如果三角形两边的平方和等于第三边的平方,那么这个三角形是直角三角形
分析：(1)构造一个直角三角形△DFE， 使∠E=90°，DE=AC，FE=BC； (2)证明△DFE与△ABC全等， (3)根据全等的性质“对应角相等”得证 你能自己写出证明过程吗？
证明：作Rt△DEF，使∠E=90°，DE=AC，FE=BC， 则DE2+EF2=DF2(勾股定理)． ∵AC2+BC2=AB2, DE=AC，FE=BC, ∴AB2=DF2， ∴AB=DF， ∴△ABC≌△DFE（SSS）． ∴∠C=∠E=90°, ∴△ABC是直角三角形．
已知：如图,在△ABC中,AC2+BC2=AB2.求证:△ABC是直角三角形．
如果三角形两边的平方和等于第三边平方, 那么这个三角形是直角三角形.
符号语言：∵在△ABC中，AC2+BC2=AB2.∴ △ABC是直角三角形.
这是判定直角三角形的方法之一.
(1)直角三角形的两个锐角互余； 有两个角互余的三角形是直角三角形；(2)直角三角形两条直角边的平方和等于斜边的平方； 如果一个三角形两边的平方和等于第三边的平方, 那么这个三角形是直角三角形；
观察下列两组定理,它们的条件与结论之间有怎样的关系?
一个命题的条件和结论分别是另一个命题的结论和条件．
(三)互逆命题与互逆定理
两直线平行，内错角相等；
如果小明患了肺炎,那么他一定会发烧；如果小明发烧,那么他一定患了肺炎；
内错角相等，两直线平行；
一个三角形中相等的边所对的角相等；一个三角形中相等的角所对的边相等；
每组命题的条件和结论有类似的关系吗？
在两个命题中，如果一个命题的条件和结论是另一个命题的结论和条件，那么这两个命题叫做互逆命题. 其中一个叫做另一个的逆命理．
逆命题：如果两个有理数的平方相等,那么这两个有理数相等”.
命题“如果两个有理数相等,那么它们的平方相等”
思考：它们都是真命题吗?
一个命题是真命题,它逆命题却不一定是真命题
条件：两个有理数相等结论：这两个有理数的平方相等
如果一个定理的逆命题也是定理，那么这两个定理叫做互逆定理，其中的一个定理叫做另一个定理的逆定理.
注意：(1)不是所有的定理都有逆定理 （2）逆定理、互逆定理，一定是真命题.
定理：直角三角形的两个锐角互余；定理：有两个角互余的三角形是直角三角形；
勾股定理及其逆定理，也是互逆定理
例1：如图，在△ABC中，AB＝AC，BD为AC边上的高，BD＝4，CD＝2，求AD的长度.
解：设AD＝a，∵AB＝AC，CD＝2，∴AB＝AC＝AD+DC＝a+2，∵BD是AC边上的高，在Rt△ABD中，AB2＝AD2+BD2，即（a+2）2＝a2+42，解得a＝3，∴AB=3
知识点一：直角三角形的性质
例2：如图，已知D是线段BC的延长线上一点，∠ACD＝∠ACB，∠COD＝∠B，求证：△AOE是直角三角形．
证明：∵∠ACD+∠ACB＝180°，∠ACD＝∠ACB，∴∠ACD＝∠ACB＝90°，∵∠AOE＝∠COD，∠COD＝∠B，∴∠AOE＝∠B，∵∠BAC+∠B＝90°，∴∠BAC+∠AOE＝90°，∴∠AEO＝90°， 即△AOE是直角三角形．
知识点二：直角三角形的判定
例4：写出下列命题的逆命题，并判断逆命题的真假
(1)同旁内角互补，两直线平行.
逆命题：两直线平行，同旁内角互补.
(2)有两个角相等的三角形是等腰三角形.
逆命题：如果一个三角形是等腰三角形，那么它有两个角相等.
（3）全等三角形的对应角相等.
逆命题：如果两个三角形的对应角相等，那么这两个三角形全等.
1．如图，点E是△ABC中AC边上的一点，过E作ED⊥AB，垂足为D，若∠1＝∠2，则△ABC是（　　）
A．直角三角形B．锐角三角形C．钝角三角形D．无法确定
2．如图，∠ACB＝90°，CD⊥BC于点D，∠BCD＝32°，则∠A的度数是（　　） A．28° B．30° C．32° D．36°
3．△ABC的三边分别为a，b，c，则无法判断△ABC为直角三角形的是（　　） A．b2＝a2﹣c2 B．∠A＝∠B+∠C C．a：b：c＝3：4：5 D．a：b：c＝1：2：3
4．如图，在△ABC中，AB＝AC＝10，BC＝12，AD是△ABC的中线，则AD长为（　　）
A．2B．6C．8D．2
5．下列正确叙述的个数是（　　）①每个命题都有逆命题②真命题的逆命题是真命题③假命题的逆命题是真命题④每个定理都有逆定理⑤每个定理一定有逆命题A．1B．2 C．3 D．4
6.写出下列命题的逆命题，并判断每对命题的真假
（2）如果ab=0，那么a=0，b=0
逆命题：如果a=0，b=0，那么ab=0
（1）如果一个整数的个位数字是5 ，那么这个整数能被5整除.
逆命题：如果一个整数能被5整除，那么这个整数的个位数字是5.
7.如图，在△ABC中，CD⊥AB于点D，AC＝20，BC＝15，DB＝9，求AD的长.
8. 如图，在△ABC中，已知AB=13cm，BC=10cm，BC边上的中线AD=12cm，求证:AB=AC.
证明:∵BD=CD，BC=10cm，∴ BD=5cm.∴ 在△ABD中, AD2+BD2=122+52＝144+25=169, AB2=132=169∴AD2+BD2=AB2.∴△ABD是直角三角形在Rt△ADC中 ∴AC2=DC2+AD2=122+52＝144+25=169,∴AC2=AB2∴AB=AC
一个定理的逆命题也是定理，这两个定理叫做互逆定理
第一个命题的条件是第二个命题的结论；第一个命题的结论是第二个命题的条件.
完成课本P17习题1.5中第1、2、3、4、5题