

数学八年级上册第三章 勾股定理3.1 勾股定理精练
展开一、选择题(本大题共8小题,每小题3分,共24分)
1.在△ABC中,若AC2-BC2=AB2,则( )
A.∠A=90° B.∠B=90°
C.∠C=90° D.不能确定
2.直角三角形的三边长分别为2,4,x,则x的值有( )
A.1个 B.2个 C.3个 D.4个
3.下列各组数中,是勾股数的一组是( )
A.0.3,0.4,0.5 B.8,15,17
C.16,18,110 D.3,4,4
4.(2023江苏泰州兴化期中)如图,在四个全等的直角三角形与一个小正方形拼成的大正方形图案中,如果大正方形的面积为16,小正方形的面积为4,直角三角形的两直角边长分别为a和b,那么(a+b)2的值为( )
A.25 B.28 C.16 D.48
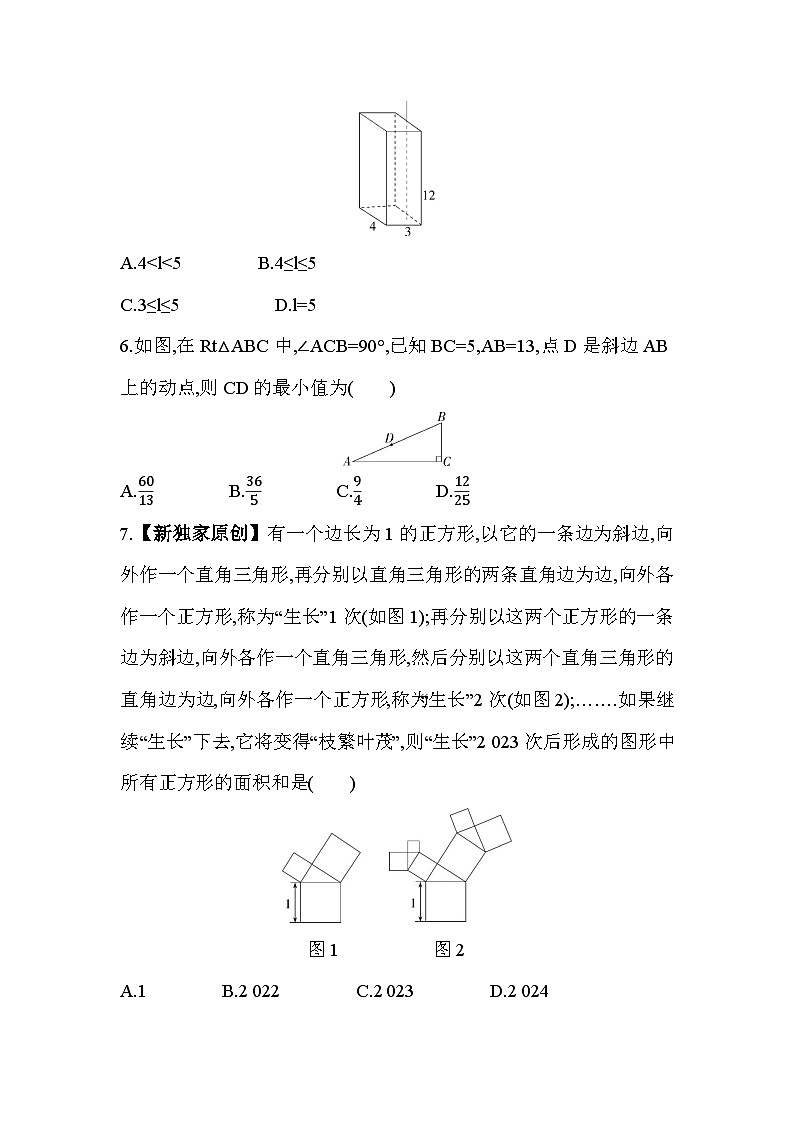
5.【教材变式·P91T5】下图是一种饮料的包装盒,长、宽、高分别为4 cm、3 cm、12 cm,现有一长为17 cm的吸管插入到盒的底部,则吸管露在盒外部分的长l (cm)的取值范围为( )
A.4
6.如图,在Rt△ABC中,∠ACB=90°,已知BC=5,AB=13,点D是斜边AB上的动点,则CD的最小值为( )
A.6013 B.365 C.94 D.1225
7.【新独家原创】有一个边长为1的正方形,以它的一条边为斜边,向外作一个直角三角形,再分别以直角三角形的两条直角边为边,向外各作一个正方形,称为“生长”1次(如图1);再分别以这两个正方形的一条边为斜边,向外各作一个直角三角形,然后分别以这两个直角三角形的直角边为边,向外各作一个正方形,称为“生长”2次(如图2);…….如果继续“生长”下去,它将变得“枝繁叶茂”,则“生长”2 023次后形成的图形中所有正方形的面积和是( )
图1 图2
A.1 B.2 022 C.2 023 D.2 024
8.如图,在△ABC中,∠BAC=90°,AB=6,BC=10,BD平分∠ABC,若P,Q分别是BD,AB上的动点,则PA+PQ的最小值是( )
A.2.4 B.4.8 C.4 D.5
二、填空题(本大题共10小题,每小题3分,共30分)
9.(2021湖南岳阳中考)《九章算术》是我国古代数学名著,书中有下列问题:“今有户高多于广六尺八寸,两隅相去适一丈.问户高、广各几何?”其意思:今有一门,高比宽多6尺8寸,门对角线的长恰好为1丈.问门高、宽各是多少?如图,设门高AB为x尺,根据题意,可列方程为 .(1丈=10尺,1尺=10寸)
10.【教材变式·P80T2】小明和小丽正在玩纸片,小明将一块正方形纸片ABCD放在地面上,小丽将另一块正方形纸片CEFG也放在地面上,使其一个顶点与纸片ABCD的一个顶点重合,且∠CGD=90°,如图所示,现量得DG的长为7 cm,设正方形ABCD的面积为S1,正方形CEFG的面积为S2,则S1-S2= .
11.【尺规作图】(2022辽宁朝阳中考)如图,在Rt△ABC中,∠ACB=90°,AB=13,BC=12,分别以点B和点C为圆心、大于12BC的长为半径作弧,两弧相交于E,F两点,作直线EF交AB于点D,连接CD,则△ACD的周长是 .
12.如图所示的网格是正方形网格(每个小正方形的边长为1),则∠PAB+∠PBA= °(点A,B,P在小正方形的顶点上).
13.(2022黑龙江牡丹江中考)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB,AC=6,BC=8,则CD= .
14.【规律探究试题】观察下列各组勾股数:①3,4,5;②5,12,13;
③7,24,25;④9,40,41;…….若a,144,145是其中的一组勾股数,则a= . 提示:5=32+12,13=52+12
15.(2022江苏徐州中考)如图,将长方形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .
16.(2023江苏南京秦淮月考)小明将4个全等的直角三角形拼成如图所示的五边形,添加适当的辅助线后,用等面积法建立等式证明勾股定理.小明在证题中用两种方法表示五边形的面积,分别是①S= ,②S= .
17.(2023江苏无锡期中)如图,在△ABC中,AB=3,AC=5,AD是边BC上的中线,AD=2,则△ACB的面积是 .
18.如图,圆柱形玻璃杯的高为7 cm,底面周长为16 cm,在杯内离杯底2 cm的点C处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿1 cm与蜂蜜相对的点A处,则蚂蚁到达蜂蜜处的最短路程为
cm.
三、解答题(本大题共6小题,共46分)
19.(2023江苏南京鼓楼期末)(6分)如图,在△ABC中,∠BAC=90°,AB=15,AC=20,AD⊥BC,垂足为D.求AD,BD的长.
20.【教材变式·P87习题T2】(7分)如图,星光蔬菜园要修建20个蔬菜大棚,棚高h=5 m,棚宽a=12 m,棚的长d为25 m,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米的塑料薄膜.
21.(7分)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形按如图所示的方式摆放时,也可以用面积法来证明勾股定理,请写出证明过程.(提示:BD和AC都可以分割四边形ABCD)
22.【最短距离问题】(2023江苏徐州期中)(8分)如图,在△ABC中,AB=10,AC=6,BC=8,点D是AB的中点,连接CD.
(1)若∠B=α,求∠DCA的度数(用含α的代数式表示);
(2)若点E是AB边上的一个动点,则线段CE的长的最小值为 .
23.【数学文化】(2023江苏扬州江都二模)(8分)清代扬州数学家罗士琳痴迷研究勾股定理,提出推算勾股数的“罗士琳法则”.其中有一个法则是“如果k是大于2的偶数,那么k和k的一半的平方减1,k的一半的平方加1是一组勾股数”.
(1)按照这个法则,写出2组不同的勾股数: , (最大数不超过18);
(2)用含有k的等式表示这三个勾股数的数量关系并证明.
24.(2022江苏南京期末)(10分)【知识生成】通过不同的方法表示同一图形的面积,可以探求相应的等式,两个边长分别为a,b的直角三角形和一个两条直角边长都是c的直角三角形拼成如图①所示的梯形,请用两种方法计算梯形面积.
(1)方法一可表示为 ;
方法二可表示为 ;
(2)根据方法一和方法二,得出a,b,c之间的数量关系是
(等式的两边需写成最简形式);
(3)若一直角三角形的两条直角边的长为6和8,则其斜边长为 ;
【知识迁移】通过不同的方法表示同一几何体的体积,也可以探求相应的等式.图②是棱长为a+b的正方体,被如图所示的分割线分成8块.
(4)用不同方法计算这个正方体的体积,就可以得到一个等式,这个等式为 ;
(5)已知2m-n=4,mn=2,利用(4)中的规律求8m3-n3的值.
图① 图②
(5)本实验对你有怎样的启示?
( 写出一条即可)。
答案全解全析
1.B ∵AC2-BC2=AB2,
∴AC2=BC2+AB2,
∴∠B=90°.故选B.
2.B 当x为斜边长时,x2=22+42=20;当4为斜边长时,x2=42-22=12.故x的值有2个.
3.B A.0.3,0.4,0.5,都不是正整数,不是勾股数,不符合题意;
B.82+152=172,能构成直角三角形,都是整数,是勾股数,符合题意;
C.16,18,110,都不是正整数,不是勾股数,不符合题意;
D.32+42≠42,故不是勾股数,不符合题意.故选B.
4.B ∵大正方形的面积为16,
∴它的边长为4,
即得a2+b2=42=16.
由题意知4×12ab+4=16,∴2ab=12,
∴(a+b)2=a2+2ab+b2=16+12=28.
故选B.
5.B ①当吸管垂直于底面时,吸管露在盒外部分最长,为17-12=5(cm);
②当插入盒内的吸管与底面对角线和高正好组成直角三角形时,吸管露在盒外部分最短,
底面对角线的长为32+42=5(cm),高为12 cm,设盒里面吸管长为x cm,
由勾股定理可得x2=52+122=169,∴x=13,
则露在盒外的吸管最短为17-13=4(cm).
故吸管露在盒外部分的长l的取值范围为4≤l≤5.
故选B.
6.A 在Rt△ABC中,∠ACB=90°,BC=5,AB=13,
∴AC2=AB2-BC2=132-52=144,∴AC=12.
当CD⊥AB时,CD的值最小,
为12AC·BC12AB=12×513=6013.故选A.
7.D 如图,
由题意得SA=1.
由勾股定理,得SB+SC=1,
∴“生长”1次后形成的图形中所有正方形的面积和为2.
同理可得,“生长”2次后形成的图形中所有正方形的面积和为3,
“生长”3次后形成的图形中所有正方形的面积和为4,
……
∴“生长”2 023次后形成的图形中所有正方形的面积和是2 024.故选D.
8.B 如图所示,作点Q关于直线BD的对称点Q',因为BD平分∠ABC,所以点Q'在BC上,连接PQ',则PA+PQ的最小值即为PA+PQ'的最小值,∴当A、P、Q'三点共线且AQ'⊥BC时,PA+PQ的值最小,过点A作AM⊥BC于点M,则PA+PQ的最小值即为AM的长.
∵AB=6,BC=10,∴由勾股定理得AC2=BC2-AB2=102-62=82,
∴AC=8,∵S△ABC=12AM·BC=12AB·AC,∴AM=AB·ACBC=4810=4.8.故选B.
9.答案 x2+(x-6.8)2=102
解析 门高AB为x尺,则门的宽为(x-6.8)尺,AC=1丈=10尺,
由勾股定理,得AB2+BC2=AC2,
即x2+(x-6.8)2=102.
10.答案 49 cm2
解析 在Rt△CDG中,由勾股定理得CD2-CG2=DG2,
∵DG=7 cm, ∴CD2-CG2=72=49.
∵S1=CD2,S2=CG2,
∴S1-S2=CD2-CG2=49(cm2).
11.答案 18
解析 由题意可知,直线EF为线段BC的垂直平分线,
∴CD=BD,
∵∠ACB=90°,AB=13,BC=12,
∴AC2=AB2-BC2=25,∴AC=5,
∴△ACD的周长为AC+AD+CD=AC+AD+BD
=AC+AB=5+13=18.
故答案为18.
12.答案 45
解析 如图,延长AP交网格线于D,连接BD,
则PD2=BD2=12+22=5,PB2=12+32=10,
∴PD2+DB2=PB2,PD=BD,
∴∠PDB=90°,
∴∠PAB+∠PBA=∠DPB=45°.故答案为45.
13.答案 3
解析 如图,过点D作DE⊥AB于E.
∵∠C=90°,AC=6,BC=8,
∴AB2=AC2+BC2=62+82=100,
∴AB=10.
∵AD平分∠CAB,∴CD=DE,
又∵S△ABC=12AC·CD+12AB·DE=12AC·BC.
∴12×6·CD+12×10·CD=12×6×8,
解得CD=3.
14.答案 17
解析 观察各组勾股数,根据题目中的提示可得,145=a2+12,解得a=17.
15.答案 43
解析 在长方形ABCD中,
∠A=∠D=90°,CD=AB=3,AD=BC=5.
由翻折的性质可知,FC=BC=5,EF=BE.
在Rt△CDF中,由勾股定理,得DF2=FC2-CD2=16,
∴DF=4,∴AF=AD-DF=1.
设AE=x,则BE=EF=3-x.
在Rt△AEF中,由勾股定理,得EF2=AE2+AF2,
即(3-x)2=x2+12,
解得x=43,即AE=43.
故答案为43.
16.答案 c2+ab;a2+b2+ab
解析 如图,延长AB,交CD于点E,①五边形的面积=边长为c的正方形的面积+2个全等的直角边长分别为a,b的直角三角形的面积,即S=c2+12ab·2=c2+ab;②五边形的面积=边长为a的正方形的面积+边长为b的正方形的面积+2个全等的直角边长分别为a,b的直角三角形的面积, 即S=a2+b2+12ab·2=a2+b2+ab.
17.答案 6
解析 如图,延长AD到E,使DE=AD,连接BE.
由题意知CD=BD.
在△ADC与△EDB中,AD=ED,∠ADC=∠EDB,CD=BD,
∴△ADC≌△EDB(SAS),
∴BE=AC=5,∠CAD=∠E.
又∵AE=2AD=4,AB=3,
∴BE2=AE2+AB2,
∴△ABE是直角三角形,∠EAB=90°.
∴S△ACB=2S△ABD=2×12×2×3=6.
故答案为6.
18.答案 10
解析 如图(图中数据的单位:cm),将杯子的侧面展开,作A关于EF的对称点A',连接A'C,交EF于P,作A'D⊥CF,交CF延长线于点D,连接AP,易知A'C的长为所求的最短路程,A'D=8 cm,CD=6 cm,根据勾股定理得A'C2=A'D2+CD2=82+62=102,所以A'C=10 cm,即所求的最短路程为10 cm.
19.解析 ∵∠BAC=90°,AB=15,AC=20,
∴BC2=AB2+AC2=625,
∴BC=25.
∵S△ABC=12AB·AC=12BC·AD,
∴AB·AC=BC·AD,
∴15×20=25AD,
∴AD=12.
∵AD⊥BC,∴BD2=AB2-AD2=152-122=81,
∴BD=9.
20.解析 如图,∵h=5 m,a=12 m,∠C=90°,
∴AB2=AC2+BC2=169,
∴AB=13 m,
∴要建20个蔬菜大棚需要13×25×20=6 500(m2)塑料薄膜.
答:需要6 500 m2塑料薄膜.
21.证明 如图,连接DB,过点D作DF⊥BC,交BC的延长线于点F,则DF=EC=b-a.由两三角形全等可推得∠DAB=90°.
∵S四边形ABCD=S△ACD+S△ABC=12b2+12ab,
S四边形ABCD=S△ADB+S△DCB=12c2+12a(b-a),
∴12b2+12ab=12c2+12a(b-a),
∴a2+b2=c2.
22.解析 (1)∵AB=10,AC=6,BC=8,
∴AC2+BC2=62+82=100,AB2=102=100,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,
∴∠ACB=90°.
∵点D是AB的中点,
∴CD=DB=12AB,
∴∠DCB=∠B=α,
∴∠DCA=∠ACB-∠DCB=90°-α,
∴∠DCA的度数为90°-α.
(2)当CE⊥AB时,线段CE的长取得最小值.
∵△ABC的面积=12AB·CE=12AC·BC,
∴AB·CE=AC·BC,
∴10CE=6×8,
∴CE=4.8,
∴线段CE的长的最小值为4.8.
23.解析 (1)当k=4时,这一组勾股数是3,4,5;当k=6时,这一组勾股数是6,8,10.
故3,4,5;6,8,10这两组勾股数符合题意.(答案不唯一)
(2)当k是大于2的偶数时,
k2+12k2-12=12k2+12.
证明:∵左边=k2+12k2-12
=k2+14k2-12
=k2+116k4+1-12k2
=116k4+12k2+1,
右边=12k2+12
=14k2+12=116k4+12k2+1.
∴左边=右边,
∴等式成立.
24.解析 (1)方法一可表示为12ab+12ab+12c2;
方法二可表示为12(a+b)2.
故答案为12ab+12ab+12c2;12(a+b)2.
(2)由题意可得12ab+12ab+12c2=12(a+b)2,
整理得c2=a2+b2.故答案为c2=a2+b2.
(3)10.
(4)方法一可表示为(a+b)3;
方法二可表示为a3+3a2b+3ab2+b3.
∴等式为(a+b)3=a3+3a2b+3ab2+b3.
故答案为(a+b)3=a3+3a2b+3ab2+b3.
(5)由(4)可得(2m-n)3=8m3-12m2n+6mn2-n3
=8m3-n3-6mn(2m-n),
∵2m-n=4,mn=2,
∴64=8m3-n3-6×2×4,
∴8m3-n3=64+48=112.
初中数学苏科版八年级上册3.1 勾股定理课后作业题: 这是一份初中数学苏科版八年级上册<a href="/sx/tb_c17054_t7/?tag_id=28" target="_blank">3.1 勾股定理课后作业题</a>,共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
初中数学苏科版八年级上册3.3 勾股定理的简单应用当堂达标检测题: 这是一份初中数学苏科版八年级上册<a href="/sx/tb_c17048_t7/?tag_id=28" target="_blank">3.3 勾股定理的简单应用当堂达标检测题</a>,共10页。试卷主要包含了3 勾股定理的简单应用,2米 B,如图,一架2,A 如图,连接AC等内容,欢迎下载使用。
数学八年级上册第三章 勾股定理3.2 勾股定理的逆定理课后测评: 这是一份数学八年级上册<a href="/sx/tb_c100305_t7/?tag_id=28" target="_blank">第三章 勾股定理3.2 勾股定理的逆定理课后测评</a>,共11页。试卷主要包含了2 勾股定理的逆定理,【新定义型试题】阅读理解等内容,欢迎下载使用。













