2024年九年级数学中考复习《将军饮马最值问题》专题提升训练（含答案）

这是一份2024年九年级数学中考复习《将军饮马最值问题》专题提升训练（含答案），共28页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．已知线段AB及直线l，在直线上确定一点，使最小，则下图中哪一种作图方法满足条件（ ）．
A．B．
C．D．
2．如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是边AC上一点，若AE＝2，则EM＋CM的最小值为（ ）
A．B．3C．2D．4
3．已知，在内有一定点P，点M，N分别是，上的动点，若的周长最小值为3，则的长为（ ）
A．B．3C．D．
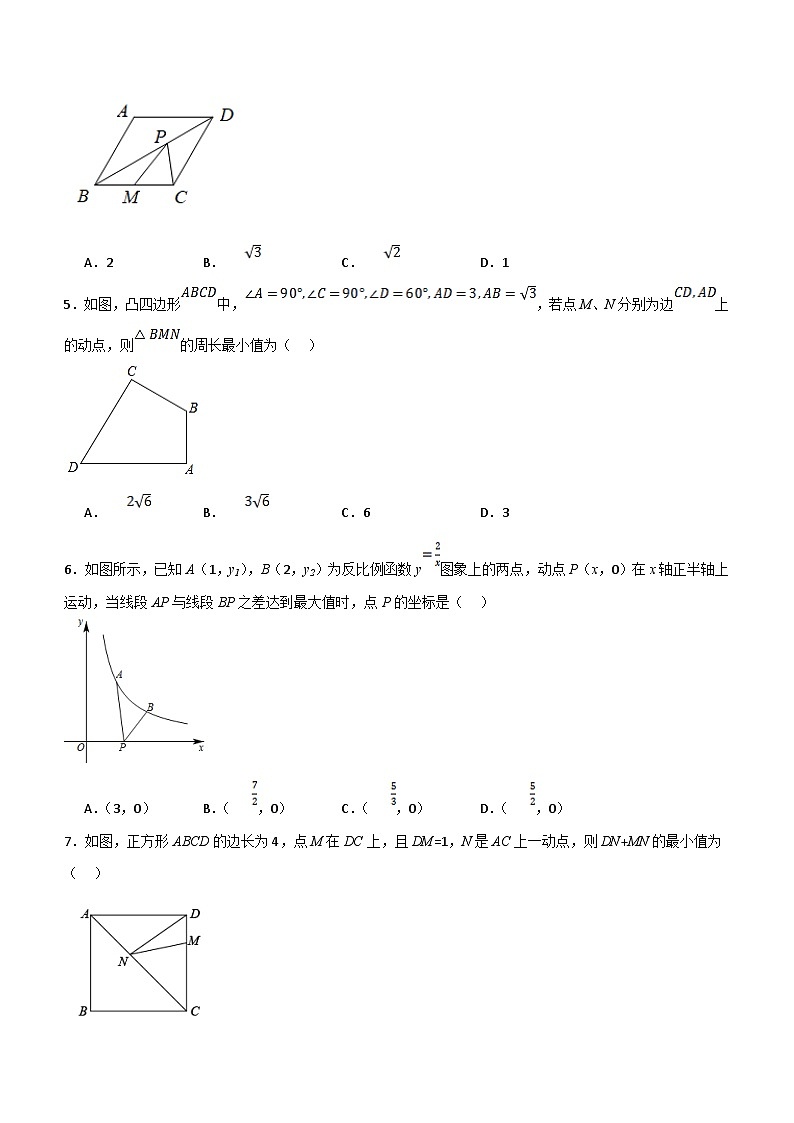
4．如图，点M是菱形ABCD的边BC的中点，P为对角线BD上的动点，若AB＝2，∠A＝120°，则PM＋PC的最小值为（ ）
A．2B．C．D．1
5．如图，凸四边形中，，若点M、N分别为边上的动点，则的周长最小值为（ ）
A．B．C．6D．3
6．如图所示，已知A（1，y1），B（2，y2）为反比例函数y图象上的两点，动点P（x，0）在x轴正半轴上运动，当线段AP与线段BP之差达到最大值时，点P的坐标是（ ）
A．（3，0）B．（，0）C．（，0）D．（，0）
7．如图，正方形ABCD的边长为4，点M在DC上，且DM=1，N是AC上一动点，则DN+MN的最小值为（ ）
A．4B．C．D．5
8．如图，的半径为2，圆心M的坐标为，点P是上的任意一点，，且、与x轴分别交于A、B两点，若点A、点B关于原点O对称，则的最小值（ ）
A．3B．4C．5D．6
二、填空题
9．如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km处，他想把他的马牵到小河边去饮水，然后回家，他要完成这件事情所走的最短路径是 km．
10．如图所示，在中，，直线EF是AB的垂直平分线，D是BC的中点，M是EF上一个动点，的面积为12，，则周长的最小值是 ．
11．如图，在矩形ABCD中，AB＝10，BC＝5．若点M、N分别是线段AC，AB上的两个动点，当BM＋MN取最小值时△BMN的周长为 ．
12．如图，在四边形ABCD中，∠BCD＝50°，∠B＝∠D＝90°，在BC、CD上分别取一点M、N，使△AMN的周长最小，则∠MAN＝ °．
13．如图，正△ABC的边长为2，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD+CD的最小值是 ．
14．如图，正方形中，点是边上一定点，点、、分别是边、、上的动点，若，则四边形的周长最小时 ．

15．如图，直线与轴，轴分别交于和，点、分别为线段、的中点，为上一动点，当的值最小时，点的坐标为 ．

16．如图，抛物线与x轴分别交于两点（点在点的左侧），与轴交于点，在其对称轴上有一动点，连接，则周长的最小值是 ．
三、解答题
17．如图，在平面直角坐标系中，每个小正方形的边长均为1，点A的坐标为．点B的坐标为，点C的坐标为．

(1)作出关于y轴对称的，其中，，分别是A，B，C的对应点；
(2)写出的坐标；
(3)在x轴上找一点P，使得的值最小．（保留作图痕迹）
18．如图，，两个村庄在河的同侧，两村庄的距离为千米，，它们到河的距离分别是1千米和3千米，为了解决这两个村庄的饮水问题，乡政府决定在河边上修建一水厂向，两村输送水．

(1)在图上作出向，两村铺设水管所用材料最省时的水厂位置．（只需作图，不需要证明）
(2)经预算，修建水厂需30万元，铺设水管的所有费用平均每千米为3万元，其他费用需5万元，求完成这项工程乡政府投入的资金至少为多少万元．
19．如图，以矩形的顶点为原点，所在的直线为轴，所在的直线为轴，建立平面直角坐标系．已知，，点是的中点，在上取一点，将沿翻折，使点落在边上的点处．

(1)直接写出点、的坐标；
(2)连接交于点，求的面积．
(3)在轴、轴上是否分别存在点、，使得四边形的周长最小？如果存在，求出周长的最小值和直线的函数解析式；如果不存在，请说明理由．
20．已知抛物线与轴相交于A、B两点（点A在点B右侧），与轴相交于点C，点，．
(1)求抛物线的顶点坐标；
(2)若点是第二象限内抛物线上一动点，过点作线段轴，交直线于点，当线段取得最大值时，求此时点的坐标．
(3)若取线段的中点，向右沿轴水平方向平移线段，得到线段，当取得最小值时，求此时点的坐标
21．几何模型：
条件：如图1，A、B是直线l同旁的两个顶点．
问题：在直线l上确定一点P，使的值最小．
方法：作点关于直线的对称点，连接交于点，则的值最小（不必证明）
模型应用：
(1)如图2，已知平面直角坐标系中两定点和，P为x轴上一动点，则当的值最小时，点P的横坐标是___________，此时___________．
(2)如图3，正方形的边长为2，为的中点，是上一动点，连接，由正方形对称性可知，与关于直线对称，则的最小值是___________．
(3)如图4，正方形的面积为，是等边三角形，点在正方形内，在对角线上有一动点，则的最小值为___________．
(4)如图5，在菱形中，，，点是边边的中点，点，分别是，上的两个动点，则的最小值是___________．
参考答案
1．解：∵点A，B在直线l的同侧，
∴作B点关于l的对称点B'，连接AB'与l的交点为P，由对称性可知BP=B'P，
∴PA+PB=PB′+PA=AB′为最小
故选：C．
2．解：连接BE，交AD于点M，过点E作EF⊥BC交于点F，
∵△ABC是等边三角形，AD是BC边上的中线，
∴B点与C点关于AD对称，
∴BM＝CM，
∴EM＋CM＝EM＋BM＝BE，此时EM＋CM的值最小，
∵AC＝6，AE＝2，
∴EC＝4，
在Rt△EFC中，∠ECF＝60°，
∴FC＝2，EF＝2，
在Rt△BEF中，BF＝4，
∴BE＝2，
故选：C．
3．解：作P关于的对称点D，作P关于的对称点E，连接交于M，交于N，连接，则此时的周长最小，

连接，
∵P、D关于对称，
∴，
同理，
∴，
∵P、D关于对称，
∴，
∵，
∴，
同理，
∴，
∵，
∴是等边三角形，
∴，
∵的周长是，
∴
故选：B．
4．解：连接AM、AC，AM交BD于P，
此时PM+PC最小，连接CP，
∵四边形ABCD是菱形，
∴OA=OC，AC⊥BD，
∴C和A关于BD对称，
∴AP=PC，
∵∠A=120°，
∴∠ABC=60°，
∴△ABC是等边三角形，
∴AC=AB=2，
∵M是BC的中点，
∴AM⊥BC，
∴∠BAM=30°，
∴BM=1，
∴AM=，
∴PM+PC=AM=．
故选B．
5．解：作点关于、的对称点分别为点和点，
连接交和于点和点，，连接、；
再和上分别取一动点和（不同于点和，
连接，，和，如图1所示：
，
，，
，
又，
，，
，
时周长最小；
连接，过点作于的延长线于点，
如图示2所示：
在中，，，
，
，
，，
又，
，
，，
，
，
又，
，
，，
在△中，由勾股定理得：
．
，
故选：C．
6．解：∵把A（1，y1），B（2，y2）代入反比例函数y得：y1＝2，y2＝1，
∴A（1，2），B（2，1），
∵在△ABP中，由三角形的三边关系定理得：|AP﹣BP|＜AB，
∴延长AB交x轴于P′，当P在P′点时，PA﹣PB＝AB，
即此时线段AP与线段BP之差达到最大，
设直线AB的解析式是y＝kx+b，
把A、B的坐标代入得：，
解得：k＝﹣1，b＝3，
∴直线AB的解析式是y＝﹣x+3，
当y＝0时，x＝3，
即P（3，0）．
故选：A．
7．解：∵四边形ABCD是正方形，
∴点B与D关于直线AC对称，
∴DN=BN，
连接BD，BM交AC于N′，连接DN′，
∴当B、N、M共线时，DN+MN有最小值，则BM的长即为DN+MN的最小值，
∴AC是线段BD的垂直平分线，
又∵CD=4，DM=1
∴CM=CD-DM=4-1=3，
在Rt△BCM中，BM=
故DN+MN的最小值是5．
故选：D．
8．解：连接，∵，∴，∵，∴，
要使取得最小值，则需取得最小值，
连接，交于点，当P位于位置时，取得最小值，
过点M作轴于点Q，
则，
∴ ，
又，
∴，
∴，
故选D．
9．解：如图，做出点A关于小河MN的对称点A`，连接A`B交MN于点P，则A`B就是牧童要完成这件事情所走的最短路程长度．
在Rt△A`DB中，由勾股定理求得．
则他要完成这件事情所走的最短路程是17km．
10．解：如图所示，连接AD，AM，
∵EF是线段AB的垂直平分线，
∴AM=BM，
∴△BDM的周长=BD+BM+DM=AM+DM+BD，
∴要想△BDM的周长最小，即要使AM+DM的值最小，
∴当A、M、D三点共线时，AM+DM最小，即为AD，
∵AB=AC，D为BC的中点，
∴AD⊥BC，，
∴，
∴AD=6，
∴△BDM的周长最小值=AD+BD=8，
故答案为：8．
11．解：如图作点B关于AC的对称点B′，连接B′A交DC于点E，则BM+MN的最小值等于的最小值，
∴当时，取得最小值，
∴作交于，则即的最小值；
∵四边形ABCD是矩形，
∴，，
∴，
又∵，
∴，
∴，
设，
∴在中，，即，
解得：，
，
设中边上的高为h，
由对称性可得，，
∴，解得：，
h+5=8，即BM+MN的最小值是8，
∴在中，，
∴，
∴△BMN的周长＝．
故答案为：12
12．解：如图，作点A关于BC、CD的对称点A1、A2，连接A1、A2分别交BC、DC于点M、N，连接AM、AN，则此时△AMN的周长最小，
∵∠BCD＝50°，∠B＝∠D＝90°，
∴∠BAD＝360°﹣90°﹣90°﹣50°＝130°，
∴∠A1+∠A2＝180°﹣130°＝50°，
∵点A关于BC、CD的对称点为A1、A2，
∴NA＝NA2，MA＝MA1，
∴∠A2＝∠NAD，∠A1＝∠MAB，
∴∠NAD+∠MAB＝∠A1+∠A2＝50°，
∴∠MAN＝∠BAD﹣（∠NAD+∠MAB）
＝130°﹣50°
＝80°，
故答案为：80．
13．解：如图，连接D，
∵正△ABC的边长为2，△ABC与△A′BC′关于直线l对称，
∴∠ABC=∠B=60°，B=AB=BC=2，
∴∠CB=60°，
∴∠CB=∠B，
∵BD=BD，
∴△CBD≌△BD，
∴CD=D，
∴AD+CD=D+CD，
∴当A、D、三点共线时，AD+CD最小，此时AD+CD=B+AB=4，
故答案为：4．
．
14．解：如图，作点G关于的对称点，作点关于的对称点，作点关于的对称点，连接交于点，交于点，连接，交于点，连接、，四边形的周长最小，

由对称的性质知，，
∴，当、、三点共线时值最小；
同理可得：，当、、、四点点共线时值最小；
∵，正方形是正方形；
∴，，
由对称的性质知，，，，，，
∴，
∵，
∴是等腰直角三角形，
∴．
∴
故答案为：．
15．解：直线与轴，轴分别交于和，
∴当，，即；当，，即，
∵点、分别为线段、的中点，
∴，，
如图所示，过点关于轴的对称点，
∴，
∴直线的解析式为：，
当，，即，
故答案为：．
16．解：抛物线与x轴分别交于两点（点在点的左侧），与轴交于点，
当时，解得或，即；当时，，即，
由二次函数对称性，关于对称轴对称，即，
，
，
周长的最小值就是的最小值，
根据两点之间线段最短即可得到的最小值为三点共线时线段长， ，
周长的最小值为 ，
故答案为：．
17．解：（1）如图即为所求；

（2）点的坐标为；
（3）如图，点P即为所求作．
18．（1）解：如图，作点关于直线的对称点，连接，交于点，

即为所求．
（2）如图，连接交于点，过点作，

由题意可知，，，
∴，
∴在中，，
∴在中，，
由对称性质可知，即
即完成这项工程乡政府投入的资金至少为（万元）．
19．（1）解：∵，，
∴点 ， 点 ，点 ，
∵点是的中点，
∴点 ；
∵将沿翻折，使点落在边上的点处．
∴，，
点 ；
（2）∵沿翻折，使点落在边上的点处．
∴，
∴，，
即：，
∴
，
∴，即：
∵，
∴，
∴的面积为；

（3）在轴、轴上存在点、，使得四边形的周长最小；
如图，作点关于轴的对称点为，点关于轴的对称点为，连接，与轴、轴上交于点、点，此时的点、使得四边形的周长最小；

由对称性可知：点 ，点 ，，，
在中，
∵，，
∴，
∴，
又∵，
；
四边形的周长最小为：；
设直线的函数解析式，
∵直线经过点 ，点 ，代入得：
，解得：
直线的函数解析式：．
20．（1）解：由题意，抛物线过，，
，
解得，
．
抛物线的顶点坐标为；
（2）解：把代入得，
∴点C坐标为．
如图，设经过，两点的直线的解析式为，
将，代入得，
解得，
∴直线的解析式为，
设点的坐标为，点的坐标为．
，
因为，
当时，有最大值．
此时，点的坐标为；
（3）解：连接，
和，
中点，
由平移得与平行且相等，
与平行且相等，
四边形是平行四边形，
．
．
作点关于轴的对称点，则，
取得最小值时，即为点，，三点共线时，
设直线的解析式为，
，解得，
直线的解析式为，
将代入得，，
此时点的坐标为．
21．解：（1）如图，取点关于轴对称的点，连接，交轴于点，作轴于，
则此时的值最小，
∵和，
∴，，，
∴，，
∵，，
∴，
∴，
∴点的横坐标为，
∵轴，
∴，
∴，
∴，
∴当的值最小时，点的横坐标是，此时；
故答案为：；；
（2）解：∵点与关于直线对称，
∴的最小值是的长，
∵正方形的边长为，为的中点，
∴，
在中，
，
∴的最小值是；
故答案为：；
（3）解：如图，设与交于点，连接，，
∵点与关于直线对称，
∴，
∴当点运动至点时，的最小值，此时最小值为的长，
∵正方形的面积为，
∴，
又∵是等边三角形，
∴，
∴的最小值为；
故答案为：；
（4）解：如图，作垂足为与交于点，
∵四边形是菱形，
∴，
∵，
∴，
∴是等边三角形，
∵是中线，
∴，
∴点关于的对称点在上，此时的最小，最小值为的长，
在中，
∵，，，
∴，
∴，
∴的最小值是．
故答案为：．