

云南省昆明市盘龙区2023-2024学年八年级上册期末数学模拟试题(附答案)
展开
这是一份云南省昆明市盘龙区2023-2024学年八年级上册期末数学模拟试题(附答案),共11页。试卷主要包含了本卷为试题卷,“白日不到处,青春恰自来,下列运算正确的是,分式的值为0,则的值是等内容,欢迎下载使用。
(本试卷三个大题,共27小题,共7页,考试时间120分钟,满分100分)
注意事项:
1.本卷为试题卷.考生必须在答题卡上解题作答.答案应书写在答题卡的相应位置上,在试题卷、草稿纸上作答无效.
2.考试结束后,请将试题卷和答题卡一并交回.
一、选择题(本大题共15个小题,每小题只有一个正确选项,每小题2分,满分30分)
1.我们生活在一个充满对称的世界中,许多建筑都具有对称性,艺术作品的创作也从对称角度考虑,自然界的许多动植物也具有对称性,中国的方块字中有些也具有对称性,对称给我们带来美的感受!这是生活之美,也是数学之美!下列现实世界中的“回收”、“节水”、“绿色食品”、“低碳”四个标志图案,是轴对称图形的是( )
A.B.C.D.
2.我国建造的港珠澳大桥全长55公里,集桥、岛、隧于一体,是世界最长的跨海大桥.如图,这是港珠澳大桥的斜拉索,它能拉住桥面,并将桥面向下的力通过钢索传给索塔,确保桥面的稳定性和安全性.那么港珠澳大桥斜拉索建设运用的数学原理是( )
A.三角形的不稳定性B.三角形的稳定性
C.四边形的不稳定性D.四边形的稳定性
3.“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”这是清朝袁枚所写五言绝句《苔》,这首咏物诗启示我们身处逆境也要努力绽放自己,要和苔花一样尽自己所能实现人生价值.苔花也被称为“坚韧之花”.袁枚所写的“苔花”很可能是苔类孢子体的苍蒴,某孢子体的苍蒴直径约为,将数据0.0000084用科学记数法表示为,则的值是( )
A.6B.C.D.
4.在平面直角坐标系中,点关于轴对称的点的坐标是( )
A.B.C.D.
5.下列运算正确的是( )
A.B.C.D.
6.下列各式由左到右的变形中,属于因式分解的是( )
A.B.
C.D.
7.如图,,,分别是的高、角平分线、中线,则下列结论错误的是( )
A.B.
C.D.
8.如图,一副三角板拼成如图所示图形,则的度数为( )
A.120°B.60°C.105°D.75°
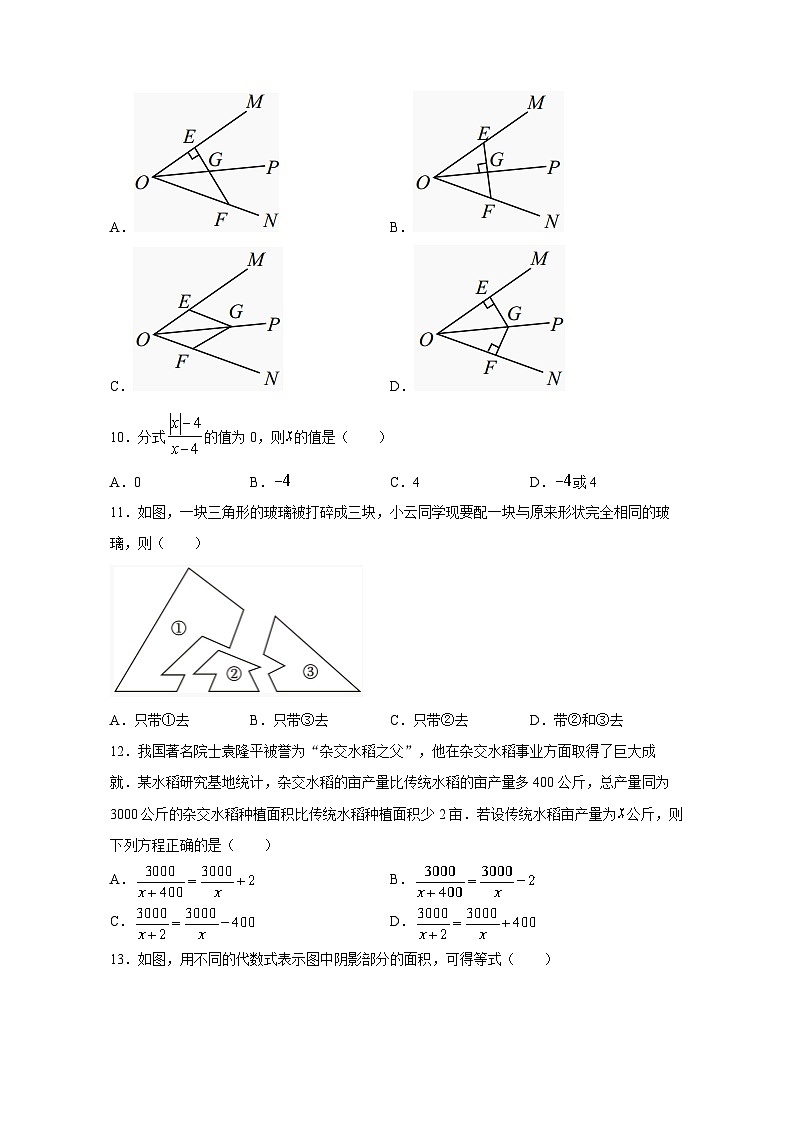
9.下列各图中,是的平分线,点,,分别在射线,,上,则可以解释定理“角的平分线上的点到角的两边的距离相等”的图形是( )
A.B.
C.D.
10.分式的值为0,则的值是( )
A.0B.C.4D.或4
11.如图,一块三角形的玻璃被打碎成三块,小云同学现要配一块与原来形状完全相同的玻璃,则( )
A.只带①去B.只带③去C.只带②去D.带②和③去
12.我国著名院士袁隆平被誉为“杂交水稻之父”,他在杂交水稻事业方面取得了巨大成就.某水稻研究基地统计,杂交水稻的亩产量比传统水稻的亩产量多400公斤,总产量同为3000公斤的杂交水稻种植面积比传统水稻种植面积少2亩.若设传统水稻亩产量为公斤,则下列方程正确的是( )
A.B.
C.D.
13.如图,用不同的代数式表示图中阴影部分的面积,可得等式( )
A.B.
C.D.
14.如图,点,在的边上.小龙同学现进行如下操作:
①以点为圆心,长为半径画弧,交于点,连接;
②以点为圆心,长为半径画弧,交于点;
③以点为圆心,长为半径画弧,交②中所画的弧于点,作射线,连接.
根据上述操作,不成立的结论是( )
A.B.
C.D.
15.如图,在中,垂直平分,分别交、于点、,平分,,,则的长为( )
A.B.C.4D.6
二、填空题(本大题共4小题,每小题2分,满分8分)
16.若一个正边形每一个外角都是60°,则______.
17.若等腰三角形的两边长分别为2和5,则这个等腰三角形的周长为______.
18.分解因式:______.
19.如图,在中,厘米,厘米,点为的中点.如果点在线段上以2厘米/秒的速度由点向点运动,同时,点在线段上由点向点运动.若点的运动速度为厘米/秒,则当与全等时,的值为______.
三、解答题(本大题共8个小题,满分62分.解答时必须写出必要的计算过程、推理步骤或文字说明.)
20.(本小题满分7分)
解方程:.
21.(本小题满分6分)
先化简,然后从,0,1,2四个数中选择一个你认为合适的数作为的值代入求值.
22.(本小题满分7分)
如图,于点,于点,.
求证:.
23.(本小题6分)
计算:(1);
(2).
24.(本小题满分8分)
如图,在平面直角坐标系中,的三个顶点的坐标分别为,,.
(1)请画出关于轴的对称图形,并写出点的坐标是______;
(2)在轴上找一点,使得周长最小,请画出;
(3)若是以为底边的等腰三角形,且点在轴上,则点的坐标是______.
25.(本小题满分8分)
“畅通交通,扮靓城市”,某市在道路提升改造中,将一段长度为720米的道路进行重新改造.为了尽快通车,某施工队在实际施工时,实际每天改造的长度是原计划每天改造长度的2倍,结果提前3天成功地完成了该段道路的改造任务,那么该施工队原计划每天改造多少米?
26.(本小题满分8分)
教科书中这样写道:“形如的式子称为完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.
配方法是一种重要的解决问题的数学方法,不仅可以将一个看似不能分解的多项式分解因式,还能解决一些与非负数有关的问题或求代数式最大值、最小值等问题.
例如:分解因式:
解:原式
再如:求代数式的最小值.
解:原式
又是一个非负数,
.
.
可知当时,有最小值,最小值是.
根据阅读材料,用配方法解决下列问题:
(1)分解因式:______;(直接写出结果)
当______时,多项式有最小值,这个最小值是______;
(2)利用配方法,已知,,为的三条边,,求的周长.
27.(本小题满分12分)
(1)如图1,在中,,,直线经过点,直线,直线,垂足分别为点、.求证:;
(2)如图2,将(1)中的条件改为:在中,,、、三点都在直线上,并且有,其中为任意锐角或钝角.结论是否仍然成立?如成立,请你给出证明;若不成立,请说明理由;
(3)如图3,、是、、三点所在直线上的两动点(、、三点互不重合),点为平分线上的一点,且和均为等边三角形,连接、,若,试判断的形状,并说明理由.
八年级数学答案
一、选择题(本大题共15个小题,每小题只有一个正确选项,每小题2分,满分30分)
二、填空题(本大题共4个小题,每小题2分,满分8分)
三、解答题(本大题共8个小题,满分62分.解答时必须写出必要的计算过程、推理步骤或文字说明.)
20.(本小题7分)解:去分母,得.
解得.
检验:当时,.
不是原分式方程的解原分式方程无解.
21.(本小题6分)解:原式
,,.
当时,原式.
22.(本小题7分)证明:,
又在和中,
.
.
(注:答案不唯一,可利用角平分线的判定定理)
23.(本小题6分)(1)解:原式.
(2)解:原式
24.(本小题8分)解:(1)如图,即为所求;
(2)如图,取点关于轴的对称点,
连接,交轴于点,连接,此时最小,
最小,即周长最小.则即为所求.
(3)或.
25.(本小题8分)解:设施工队原计划每天改造米,
根据题意得:,解得,
经检验,是原分式方程的解且符合实际意义
答:施工队原计划每天改造120米.
26.(本小题8分)解:(1) 2
(2),,为的三条边,,
,
,
,,
的周长为.
27.(本小题12分)解:(1)如图1,直线,直线,
,
,
,,
在和中,,
,,,
;
(2)成立.
如图2,,
,
,
在和中,,
,
,,
;
(3)为等边三角形.
如图3,由(2)可知,,
,,
和均为等边三角形,
,,
,
,
在和中,,
,
,,
,
为等边三角形.题号
1
2
3
4
5
6
7
8
答案
C
B
D
A
B
A
C
D
题号
9
10
11
12
13
14
15
答案
D
B
A
B
D
C
D
16
17
18
19
6
12
2或3
相关试卷
这是一份云南省昆明市九县区2023-2024学年八年级上册期末数学模拟试题(附答案),共9页。试卷主要包含了本卷为试题卷,下列运算正确的是等内容,欢迎下载使用。
这是一份云南省保山市隆阳区2023-2024学年八年级上册期末数学模拟试题(附答案),共11页。试卷主要包含了考试结束后,请将答题卡交回,下列计算正确的是,若,则的结果是,用三角尺可按下面方法画角平分线,如果实数a,b满足,那么等于等内容,欢迎下载使用。
这是一份云南省昆明市盘龙区2023-2024学年九年级上学期期末数学试题,共23页。试卷主要包含了单选题,填空题,解答题等内容,欢迎下载使用。








