初中数学北师大版九年级下册4 解直角三角形复习课件ppt

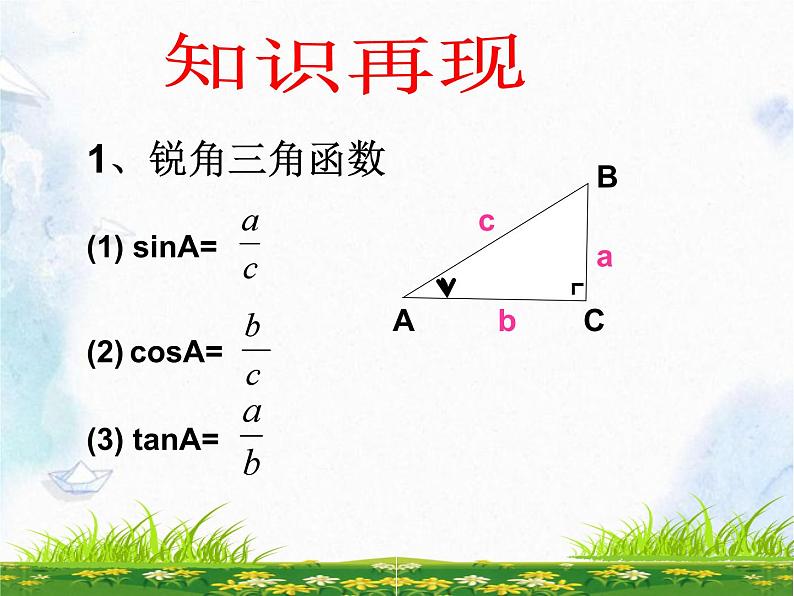
这是一份初中数学北师大版九年级下册4 解直角三角形复习课件ppt，共19页。PPT课件主要包含了考题分析，复习目标，锐角三角函数，知识再现，解题依据，中考考点等内容，欢迎下载使用。
广东试题研究：含特殊角的三角函数值的混合运算是中考重点内容；解直角三角形在实际生活中的应用是中考的重点内容，也是必考内容，求宽度、高度等问题总是轮着考.
1.熟练掌握直角三角形中蕴含的三种等量关系。2.熟记特殊角的三角函数值。3.能运用三角函数解决与直角三角形有关的简单的实际问题。
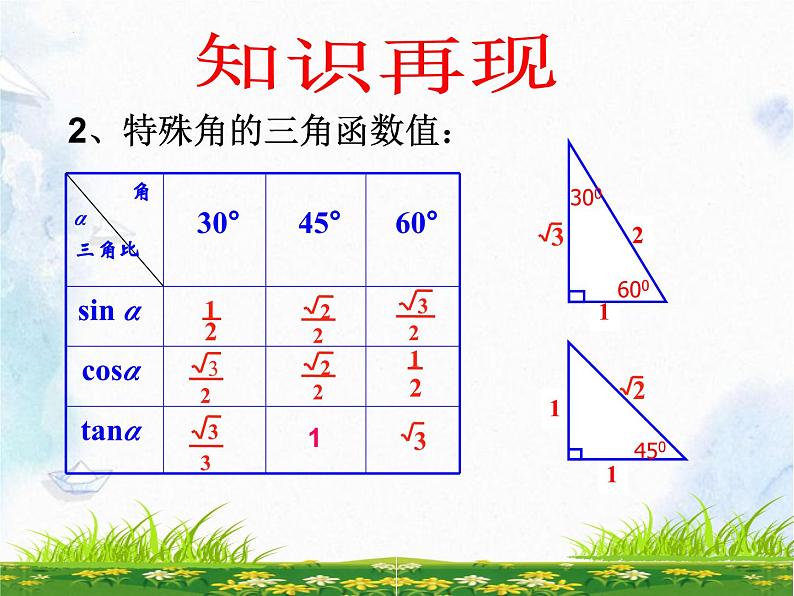
2、特殊角的三角函数值：
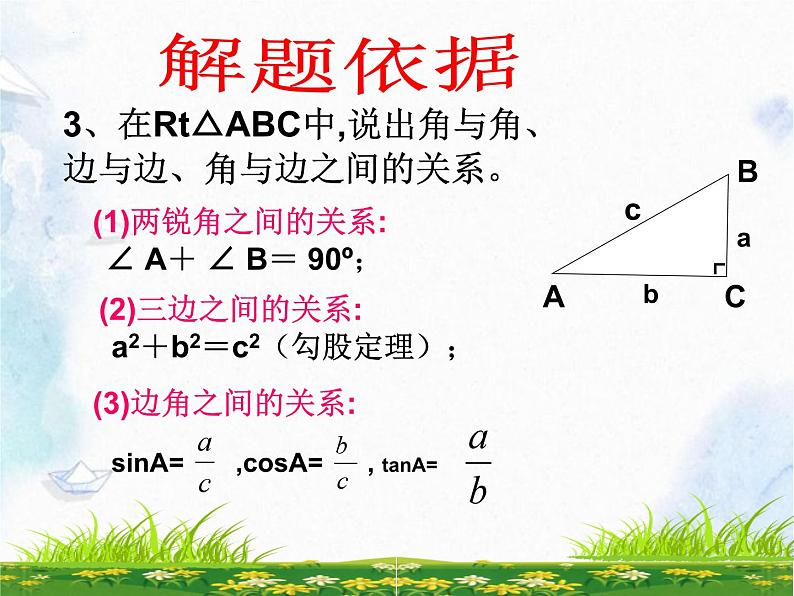
3、在Rt△ABC中,说出角与角、边与边、角与边之间的关系。
(2)三边之间的关系:
a2＋b2＝c2（勾股定理）；
(1)两锐角之间的关系:
∠ A＋ ∠ B＝ 90º；
(3)边角之间的关系:
考点精讲【例1】（2013广东）在Rt△ABC中，∠ABC=90°，AB=3，BC=4，则sinA= .　　思路点拨：首先由勾股定理求得斜边AC=5，然后由锐角三角函数的定义知sinA= ，将相关线段的长度代入计算即可.　　答案：
　　解题指导：解此类题的关键是画出图形，利用锐角三角函数的定义进行计算.　　
考题再现1. （2020汕尾）在Rt△ABC中，∠C=90°，若sinA= 则csB的值是（　　）2. （2020广州）如图6-3-1，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA等于　　（　　）
考点2 特殊角的三角函数值
【例2】（2020广东）计算： 解：原式
3.(2019年广西玉林)计算：cs245°＋sin245°＝(　　)
考点3　解直角三角形的应用
考点精讲【例3】（2020广东）如图6-3-6，某数学兴趣小组想测量一棵树CD的高度，他们先在点A处测得树顶C的仰角为30°，然后沿AD方向前行10 m，到达B点，在B处测得树顶C的仰角高度为60°（A，B，D三点在同一直线上）.请你根据他们的测量数据计算这棵树CD的高度（结果精确到0.1 m）.（参考数据： ≈1.414， ≈1.732）
　　思路点拨：首先利用三角形的外角的性质求得∠ABC的度数，得到BC的长度，然后在直角△BDC中，利用三角函数即可求解.　　解：∵∠CBD=∠A+∠ACB，　　∴∠ACB=∠CBD-∠A=60°-30°=30°.　　∴∠A=∠ACB.　　∴BC=AB=10（m）.　　在Rt△BCD中，CD=BC·sin∠CBD=10× = ≈ 5×1.732=8.7（m）.　　答：这棵树CD的高度为8.7米.
　　解题指导：解此类题的关键是借助仰角构造直角三角形并解直角三角形.　　
考题再现5.（2020•广东）如图-5，小明家在A处，门前有一口池塘，隔着池塘有一条公路l，AB是A到l的小路.现新修一条路AC到公路l，小明测量出∠ACD=30°，∠ABD=45°，BC=50m，请你帮小明计算他家到公路l的距离AD的长度（精确到0.1m)
答案：解：假设AD=x，AD⊥DC,∠ABD=45°∵AD=x，∴BD=x，∵∠ACD=30°，∠ABD=45°，BC=50m，∴tan30°= = ，∴ = ，∴AD=25（ +1）≈68.3m．答：小明家到公路l的距离AD约为68.3m.
考题再现6.（广东）如图，小山岗的斜坡AC的坡度是tanα= ，在与山脚C距离200米的D处，测得山顶A的仰角为26.6°，求小山岗的高AB（结果取整数：参考数据：sin26.6°≈0.45，cs26.6°≈0.89,tan26.6°≈0.50）．
1、本节课你有哪些收获?2、解直角三角形中你还要注意什么问题?