2023-2024学年安徽省合肥六中高新校区九年级（上）期末数学试卷（含解析）

这是一份2023-2024学年安徽省合肥六中高新校区九年级（上）期末数学试卷（含解析），共26页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1.逢年过节抑或新婚喜庆、人们把美丽鲜艳的剪纸贴在雪白的窗纸或明亮的玻璃窗上、墙上、门上、灯笼上，节日的气氛便被渲染得非常浓郁喜庆.在下列四幅剪纸中，为中心对称图形的是( )
A. B. C. D.
2.下列各组线段中，成比例的是( )
A. 2cm，3cm，4cm，5cmB. 2cm，4cm，6cm，8cm
C. 3cm，6cm，8cm，12cmD. 1cm，3cm，5cm，15cm
3.在Rt△ABC中，∠C=90°，BC=1，AC= 3，那么csB的值是( )
A. 12B. 13C. 33D. 3
4.若在反比例函数y=kx图象的任一支上，y都随x的增大而增大，则下列点可能在这个函数图象上的为( )
A. (2,0)B. (3,2)C. (−1,+2)D. (−1,−3)
5.如图所示，A、B、C、D是一个外角为40°的正多边形的顶点．若O为正多边形的中心，则∠OAD的度数为( )
A. 14°
B. 40°
C. 30°
D. 15°
6.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成一个大正方形，设直角三角形较长直角边长为a，较短直角边长为b，若ab=24，大正方形的面积为129.则小正方形的边长为( )
A. 7B. 8C. 9D. 10
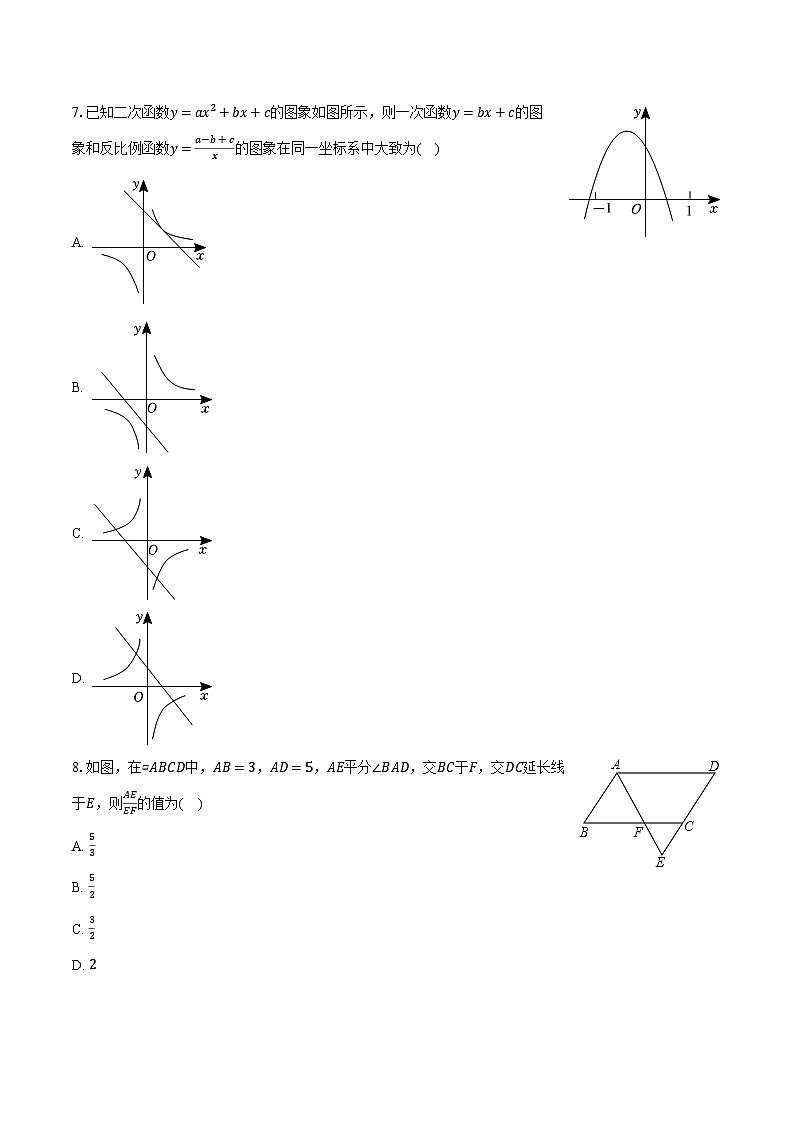
7.已知二次函数y=ax2+bx+c的图象如图所示，则一次函数y=bx+c的图象和反比例函数y=a−b+cx的图象在同一坐标系中大致为( )
A.
B.
C.
D.
8.如图，在▱ABCD中，AB=3，AD=5，AE平分∠BAD，交BC于F，交DC延长线于E，则AEEF的值为( )
A. 53
B. 52
C. 32
D. 2
9.如图，在正方形ABCD中，点E为边BC的中点，连接AC、BD、AE，且AC交BD于O，AE交BD于F，则sin∠BFE的值为( )
A. 3 1010
B. 104
C. 2 55
D. 53
10.如图，⊙O的半径为4，定点P在⊙O上，动点A，B也在⊙O上，且满足∠APB=30°，C为PB的中点，则点A，B在圆上运动的过程中，线段AC的最大值为( )
A. 3+1
B. 3−1
C. 2 3+2
D. 2 3−2
二、填空题：本题共4小题，每小题5分，共20分。
11.已知a6=b5=c4，且a+b−2c=6，则a的值为______．
12.如图，在边长为1的正方形网格中，点A、B、C、D、E都是小正方形的顶点，则图中所形成的三角形中，与△ABC相似的三角形是______．
13.如图，在△ABC和△ADE中，∠BAC=∠DAE=90°，AB=AC=4，AD=AE=3，点D在BC上，DE与AC交于点F，连接CE，则AF= ______．
14.如图，在平面直角坐标系中，等边△ABO的顶点A在第一象限，点B(5,0)，双曲线y=kx(k>0,x>0)把△ABO分成两部分，若OC=3BD．
(1)双曲线与边OA，AB分别交于C，D两点，k的值为______．
(2)连接CD，则△ACD的面积为______．
三、解答题：本题共9小题，共90分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题8分)
计算：2cs60°− 18+4cs45°+(2023−π)0．
16.(本小题8分)
羽毛球运动是一项很好的健身项目，羽毛球发球时，羽毛球飞行路线为抛物线的一部分，如图，一运动员站在O点发球，且羽毛球飞行高度y(m)与水平距离x(m)之间满足函数关系式y=−14x2+x+1．
(1)求羽毛球飞行路线中离地最大高度．
(2)已知羽毛球球网高度为1.55m，发球点A与球网的水平距离为3m，通过计算说明这次发球是否能过网？
17.(本小题8分)
如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(−2,1)、B(−3,3)、C(−1,4)．
(1)以原点O为位似中心，在第二象限内画出将△ABC放大为原来的2倍后的△A1B1C1．
(2)画出△ABC绕O点顺时针旋转90°后得到的△A2B2C2．
18.(本小题8分)
如图，为测量学校旗杆AB的高度，小明从旗杆正前方8米处的点C出发，沿坡度为i=1： 3的斜坡CD前进8米到达点D，在点D处放置测角仪，测得旗杆顶部A的仰角为37°，量得测角仪DE的高为1.5米，A、B、C、D、E在同一平面内，且旗杆和测角仪都与水平地面BC垂直．
(1)求点D的铅垂高度；
(2)求旗杆AB的高度.(结果精确到0.1米.参考数据：sin37°≈0.60，cs37°≈0.80，tan37°≈0.75， 2≈1.41， 3≈1.73.)
19.(本小题10分)
如图在△ABC中，D为BC上一点，AD平分∠BAC，AD=DC．
(1)求证：△ABC∽△DBA；
(2)若BD=2，DC=3，求AC的长．
20.(本小题10分)
如图，Rt△ABC内接于⊙O，AB为直径，过O作OD⊥AB，交BC的延长线于点D，过C作⊙O的切线交OD于点E．
(1)求证：EC=ED；
(2)若⊙O的半径为8，OE=10，求AC的长．
21.(本小题12分)
一次函数y=ax+b的图象与反比例函数y=kx的图象交于A(1,6)，B(n,−1)，与x轴交于C．
(1)求a，b，k的值；
(2)观察图象，直接写出不等式ax+b0时，在每一个象限内，y随x的增大而减小；当k0，
∴a−b=9，
即小正方形的边长为9．
故选：C．
根据大正方形的面积=4×12ab+(a−b)2=a2+b2，结合ab=24即可求解
本题考查了勾股定理的证明，正确得出大正方形的面积的两种表示方法是解题的关键．
7.【答案】A
【解析】解：∵二次函数的图象开口向下，
∴a0，
∴反比例函数y=a−b+cx的图象必在一、三象限，
故B、C、D错误，A正确；
故选：A．
先根据二次函数的图象开口向下和对称轴可知b0，由当x=−1时，y0，然后利用排除法即可得出正确答案．
本题考查的是二次函数的图像与系数的关系，反比例函数及一次函数的性质，熟知以上知识是解答此题的关键．
8.【答案】B
【解析】解：∵四边形ABCD是平行四边形，
∴AB//DE，AD//BC，
∴∠BAE=∠E，
∵AE平分∠BAD，
∴∠EAD=∠BAE，
∴∠E=∠EAD，
∴AD=DE=5，
∴CE=DE−CD=5−3=2，
∵BC/​/AD，
∴EFAE=ECDE=25，
∴AEEF=52．
故选：B．
根据平行四边形的性质得到AB//DE，然后利用平行线的性质得到∠BAE=∠E，再利用角平分线的定义得到∠EAD=∠BAE，进而得到∠E=∠EAD，从而得到DE=AD=5，则EC=5−3=2，然后利用平行线分线段成比例求解即可．
本题主要考查了相平行线分线段成比例定理以及平行四边形的性质，平行线的性质，角平分线的定义，等腰三角形的判定及性质，平行线分线段成比例，熟记平行四边形的各种性质是解题关键．
9.【答案】A
【解析】解：∵四边形ABCD是正方形，
∴AD=BC，AD//BC，AO=BO=DO，
∵点E为边BC的中点，
∴BE=12BC=12AD，
∵AD/​/BC，
∴BEAD=BFDF=12，
∴DF=2FB，
设BF=x，则DF=2x，
∴BD=3x，
∴AO=BO=DO=32x，
∴OF=12x，
∴AF= AO2+OF2= 102x，
∴sin∠BFE=sin∠AFO=AOAF=3 2x 102x=3 1010，
故选：A．
由平行线分线段成比例可求DF=2BF，由勾股定理可求AF的长，即可求解．
本题考查了正方形的性质，锐角三角函数，勾股定理，平行线分线段成比例等知识，利用参数表示线段长度是解题的关键．
10.【答案】C
【解析】解：连接OA、OB、OP，连接BA，并延长至H，使HA=AB，连接OH，PH，
∵∠APB=30°，
∴∠AOB=60°，
∵OA=OB，
∴△AOB是等边三角形，
∴∠OBA=60°，
∵OA=AH=AB，
∴∠HOB=90°，
∴OH= 3OB=4 3，
∵点C是BP的中点，A是BH的中点，
∴AC是△PBH的中位线，
∴HP=2AC，
∵HP≤OH+OP，
∴HP的最大值为4 3+4，
∴AC的最大值2 3+2，
故选：C．
连接OA、OB、OP，连接BA，并延长至H，使HA=AB，连接OH，PH，首先说明△AOB是等边三角形，再说明∠HOB=90°，利用三角形三边关系可得答案．
本题主要考查了圆周角定理，等边三角形的判定与性质，直角三角形的判定与性质，三角形中位线定理等知识，构造三角形中位线是解题的关键．
11.【答案】12
【解析】【分析】此题主要考查了比例的性质，正确表示出各数是解题关键．直接利用已知比例式假设出a，b，c的值，进而利用a+b−2c=6，得出答案．
【解答】
解：∵a6=b5=c4，
∴设a=6x，b=5x，c=4x．
∵a+b−2c=6，
∴6x+5x−8x=6，解得x=2，
故a=12．
12.【答案】△DEB
【解析】解：观察图象可知，∠BAC=∠BDE=135°，
∵AB=1，AC= 2，BD=2 2，DE=2，
∴BDAC=DEAB=2，
∴△ABC∽△DEB．
故答案为：△DEB．
利用两边成比例夹角相等，证明三角形相似．
本题考查相似三角形的判定，解题的关键是掌握相似三角形的判定方法．
13.【答案】94
【解析】解：∵∠BAC=∠DAE=90°，
∴∠BAD=∠CAE，
∵AB=AC=4，AD=AE=3，
∴△ABD≌△ACE(SAS)，∠B=∠AED=45°，
∴∠B=∠ACE=45°，
∴△AEF∽△ACE，
∴AFAE=AEAC，即AF3=34，
∴AF=94．
故答案为：94．
先证明△ABD≌△ACE，得出∠ACE=45°，由AD=AE，∠DAE=90°可得∠AEF=45°，进而证明△AEF∽△ACE，根据对应边成不了即可解答．
本题考查全等三角形的判定和性质，相似三角形的判定和性质，熟练掌握以上知识是解题关键．
14.【答案】9 34 2 3
【解析】解：(1)如图，作DH⊥x轴于H，CE⊥x轴于G，
设BD=x，
∴OC=3BD=3x．
在Rt△CEO中，∠COE=60°，
∴OE=32x，CE=3 32x.
∴C(32x,3 32x)．
在Rt△DHB中，∠B=60°，
∴BH=12x，DH= 32x.
又OB=5，
∴OH=5−12x.
∴D(5−12x, 32x)．
又C、D在y=kx上，
∴32x⋅3 32x=(5−12x)× 32x=k．
∴x=1，k=9 34．
故答案为：9 34．
(2)如图，连接CD，作AF⊥x轴于F，DG⊥AF于G．
∴DG/​/OB．
∴ADAB=DGBF．
由题意，∵OB=5，
∴A(52,5 32).
又由(1)得D(92, 32)，B(5,0)，
∴DG=92−52=2，BF=52．
∴ADAB=252=45．
连接BC．
∴S△ACD=45S△ABC，
又CE/​/AF，
∴ACOA=EFOF．
又C(32,32 3)，即OE=32，
∴EF=OF−OE=52−32=1．
∴ACOA=152=25．
∴S△ABC=25S△AOB．
∴S△ACD=825S△AOB=825× 34×25=2 3．
故答案为：2 3．
(1)依据题意，作DH⊥x轴于H，CE⊥x轴于G，设BD=x，从而OC=3BD=3x，再表示出C(32x,3 32x)，D(5−12x, 32x)，从而可得32x⋅3 32x=(5−12x)× 32，计算可以得解；
(2)依据题意，连接CD，作AF⊥x轴于F，DG⊥AF于G，从而DG//OB，进而ADAB=DGBF，再结合题意得ADAB=252=45，故可得S△ACD=45S△ABC，又由ACOA=152=25，从而S△ABC=25S△AOB，最后可以计算得解．
本题主要考查了反比例函数图象上点的坐标特征，等边三角形的性质，反比例函数系数k的几何意义，三角形的面积，正确表示线段长度的比是解题的关键．
15.【答案】解：原式=2×12−3 2+4× 22+1
=1−3 2+2 2+1
=1+1+2 2−3 2
=2− 2．
【解析】先把特殊角的三角函数值代入，再把二次根式化成最简二次根式，然后进行计算即可．
本题主要考查了实数的运算，解题关键是熟练掌握特殊角的三角函数值、零指数幂的性质和化简二次根式．
16.【答案】解：(1)由题意，∵y=−14x2+x+1=−14(x−2)2+2，
∴羽毛球飞行路线中离地最大高度为2m．
(2)由题意，令x=3，
∴y=−14(3−2)2+2=1.75．
∵1.75>1.55，
∴这次发球能过网．
【解析】(1)依据题意，将y=−14x2+x+1变形为y=−14(x−2)2+2，进而可以判断得解；
(2)依据题意，令x=3，代入求得y=−14(3−2)2+2=1.75，再由1.75>1.55，进而可以判断得解．
本题主要考查二次函数的应用，解题时要能熟练掌握并学会用待定系数法求函数解析式是关键．
17.【答案】解：(1)如图1，△A1B1C1即为所求；

(2)如图2，△A2B2C2即为所求．

【解析】(1)把点A、B、C的横纵坐标都乘以2得到A1、B1、C1的坐标，然后描点即可；
(2)利用网格特点和旋转的性质画出点A、B，C的对应点A2、B2、C2即可得到△A ​2 B 2C2．
本题考查了作图−位似变换以及旋转变换，正确掌握图形变换的性质是解题关键．
18.【答案】解：(1)延长ED交BC于点F，

由题意得：EF⊥BF，CD=8米，
∵斜坡CD的坡度为i=1： 3，
∴DFCF=1 3= 33，
在Rt△CDF中，tan∠DCF=DFCF= 33，
∴∠DCF=30°，
∴DF=12CD=4(米)，CF= 3DF=4 3(米)，
∴点D的铅垂高度为4米；
(2)过点E作EG⊥AB，垂足为G，

由题意得：EG=BF，BG=EF=DE+DF=1.5+4=5.5(米)，BC=8米，
∴EG=BF=BC+CF=(8+4 3)米，
在Rt△AEG中，∠AEG=37°，
∴AG=EG⋅tan37°≈0.75(8+4 3)=(6+3 3)米，
∴AB=AG+BG=6+3 3+5.5≈16.7(米)，
∴旗杆AB的高度约为16.7米．
【解析】(1)延长ED交BC于点F，根据题意可得：EF⊥BF，CD=8米，DFCF= 33，然后在Rt△CDF中，利用特殊角的三角函数值可得∠DCF=30°，从而利用含30度角的直角三角形的性质进行计算，即可解答；
(2)过点E作EG⊥AB，垂足为G，根据题意可得：EG=BF，BG=EF=5.5米，BC=8米，从而可得EG=BF=(8+4 3)米，然后在Rt△AEG中，利用锐角三角函数的定义求出AG的长．从而利用线段的和差关系进行计算，即可解答．
本题考查了解直角三角形的应用−仰角俯角问题，坡度坡角问题，根据题目的已知条件并结合图形添加适当的辅助线是解题的关键．
19.【答案】(1)证明：∵AD平分∠BAC，
∴∠BAD=∠CAD，
∵AD=DC，
∴∠CAD=∠C，
∴∠BAD=∠C．
∵∠B=∠B，
∴△ABC∽△DBA；
(2)解：∵BD=2，DC=3，
∴BC=5，
∵AD=DC，
∴AD=3．
∵△ABC∽△DBA，
∴ABBD=BCAB，
∴AB2=5AB，
∴AB= 10．
∵△ABC∽△DBA，
∴ACAD=ABBD，
∴AC3= 102，
∴AC=3 102．
【解析】(1)利用角平分线的定义，等腰三角形的性质和相似三角形的判定定理解答即可；
(2)利用相似三角形的性质定理解答即可．
本题主要考查了相似三角形的判定与性质，角平分线的定义，等腰三角形的性质，熟练掌握相似三角形的判定与性质是解题的关键．
20.【答案】(1)证明：连接OC，
∵CE切圆于C，
∴半径OC⊥CE，
∴∠OCE=90°，
∴∠DCE+∠OCB=90°，
∵OD⊥AB，
∴∠BOD=90°，
∴∠D+∠B=90°，
∵OB=OC，
∴∠B=∠OCB，
∴∠D=∠DCE，
∴EC=ED；
(2)解：∵∠OCE=90°，OE=10，OC=8，
∴CE= OE2−OC2=6，
∴DE=CE=6，
∴OD=OE+ED=10+6=16，
∵∠BOD=90°，OB=8，
∴BD= OD2+OB2=8 5，
∵AB是圆的直径，
∴∠ACB=90°，
∴∠ACB=∠BOD，
∵∠ABC=∠DBO，
∴△ABC∽△DBO，
∴AC：DO=AB：DB，
∴AC：16=16：8 5，
∴AC=32 55．
【解析】(1)连接OC，由切线的性质定理推出∠OCE=90°，由余角的性质推出∠D=∠DCE，即可证明EC=ED；
(2)由勾股定理求出CE= OE2−OC2=3，得到DE=CE=3，求出OD=OE+ED=5+3=8，由勾股定理求出BD= OD2+OB2=4 5，由△ABC∽△DBO，得到AC：DO=AB：DB，代入有关数据即可求出AC=16 55．
本题考查切线的性质，等腰三角形的判定，勾股定理，相似三角形的判定和性质，关键是由切线的性质得到∠OCE=90°；证明△ABC∽△DBO．
21.【答案】解：(1)∵反比例函数y=kx的图象经过A(1,6)，
∴k=1×6=6，
∵B(n,−1)，
∴6=−n，
∴n=−6，
∴B(−6,−1)，
∵点A、B在y=ax+b的图象上，
∴a+b=6−6a+b=−1，
解得：a=1b=5，
∴a=1，b=5，k=4；
(2)由图象可得：不等式ax+b