初中19.3 矩形 菱形 正方形教学设计

这是一份初中19.3 矩形 菱形 正方形教学设计，共4页。教案主要包含了教学反思等内容，欢迎下载使用。
教学设计

（续表）
【教学反思】
本节课从现实生活的正方形图案，折纸活动和纱巾的检验为切入口，让学生感知正方形在现实生活中的广泛应用；教学过程中加进了童话剧表演和探究活动，调动了大部分学生的积极性，激发了学生学习的兴趣。探索正方形的判定时，通过学生动手操作，观看几何画板，微课，感知、总结、归纳等得出结论，学生通过合作、交流、类比、归纳总结的方式得出正方形的判定，通过学生讨论、自主探究，利用小组合作的学习方式，使学生主动地去获取知识。
课堂知识容量大，教学设计有梯度，由浅入深。作业布置分层次，体现分层教学的思想。
值得改进之处：1、未能兼顾少部分学困生；
2、本节课的教学内容相对较多，灵活性也较强，所以导致学生独自思考和练习的时间不多，我会在以后的教学中加以改进。
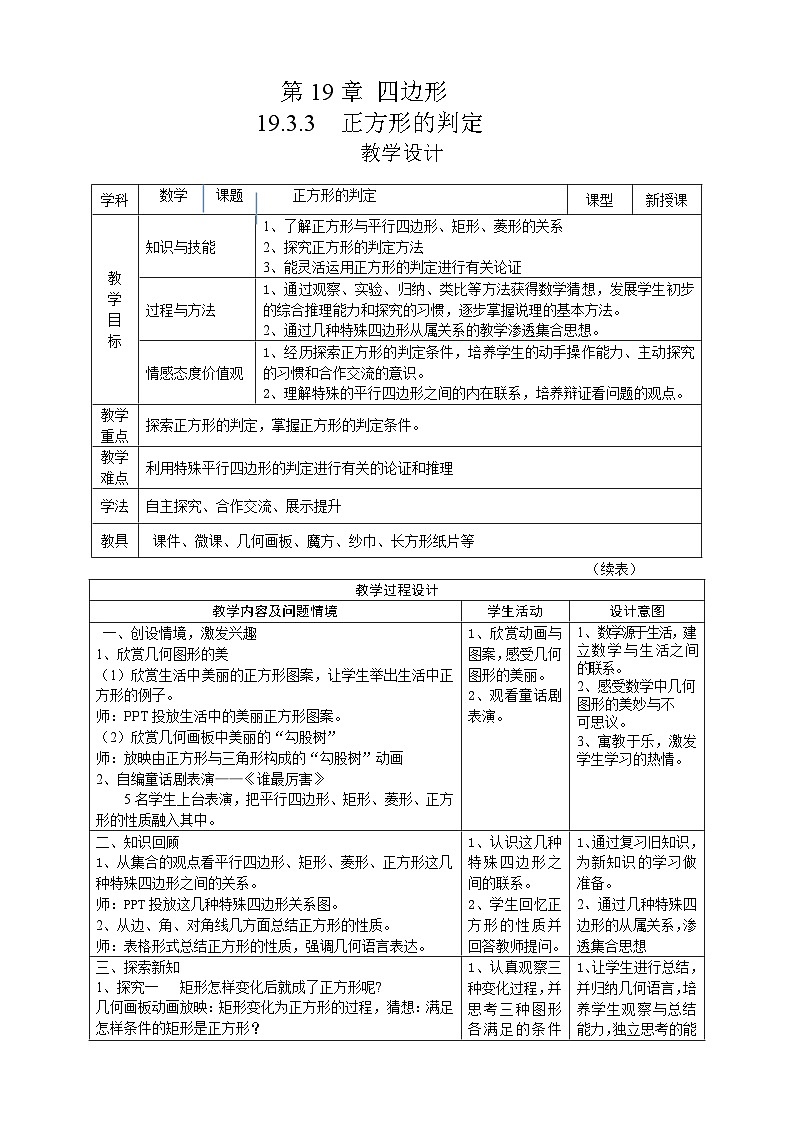
学科
数学 课题 正方形的判定
课型
新授课
教
学
目
标
知识与技能
1、了解正方形与平行四边形、矩形、菱形的关系
2、探究正方形的判定方法
3、能灵活运用正方形的判定进行有关论证
过程与方法
1、通过观察、实验、归纳、类比等方法获得数学猜想，发展学生初步的综合推理能力和探究的习惯，逐步掌握说理的基本方法。
2、通过几种特殊四边形从属关系的教学渗透集合思想。
情感态度价值观
1、经历探索正方形的判定条件，培养学生的动手操作能力、主动探究的习惯和合作交流的意识。
2、理解特殊的平行四边形之间的内在联系，培养辩证看问题的观点。
教学重点
探索正方形的判定，掌握正方形的判定条件。
教学难点
利用特殊平行四边形的判定进行有关的论证和推理
学法
自主探究、合作交流、展示提升
教具
课件、微课、几何画板、魔方、纱巾、长方形纸片等
教学过程设计
教学内容及问题情境
学生活动
设计意图
一、创设情境，激发兴趣
1、欣赏几何图形的美
（1）欣赏生活中美丽的正方形图案，让学生举出生活中正方形的例子。
师：PPT投放生活中的美丽正方形图案。
（2）欣赏几何画板中美丽的“勾股树”
师：放映由正方形与三角形构成的“勾股树”动画
2、自编童话剧表演——《谁最厉害》
5名学生上台表演，把平行四边形、矩形、菱形、正方形的性质融入其中。
1、欣赏动画与图案，感受几何
图形的美丽。
2、观看童话剧表演。
1、数学源于生活，建立数学与生活之间的联系。
2、感受数学中几何
图形的美妙与不
可思议。
3、寓教于乐，激发学生学习的热情。
知识回顾
从集合的观点看平行四边形、矩形、菱形、正方形这几种特殊四边形之间的关系。
师：PPT投放这几种特殊四边形关系图。
从边、角、对角线几方面总结正方形的性质。
师：表格形式总结正方形的性质，强调几何语言表达。
1、认识这几种特殊四边形之间的联系。
2、学生回忆正方形的性质并回答教师提问。
1、通过复习旧知识，为新知识的学习做准备。
2、通过几种特殊四边形的从属关系，渗透集合思想
三、探索新知
1、探究一 矩形怎样变化后就成了正方形呢?
几何画板动画放映：矩形变化为正方形的过程，猜想：满足怎样条件的矩形是正方形？
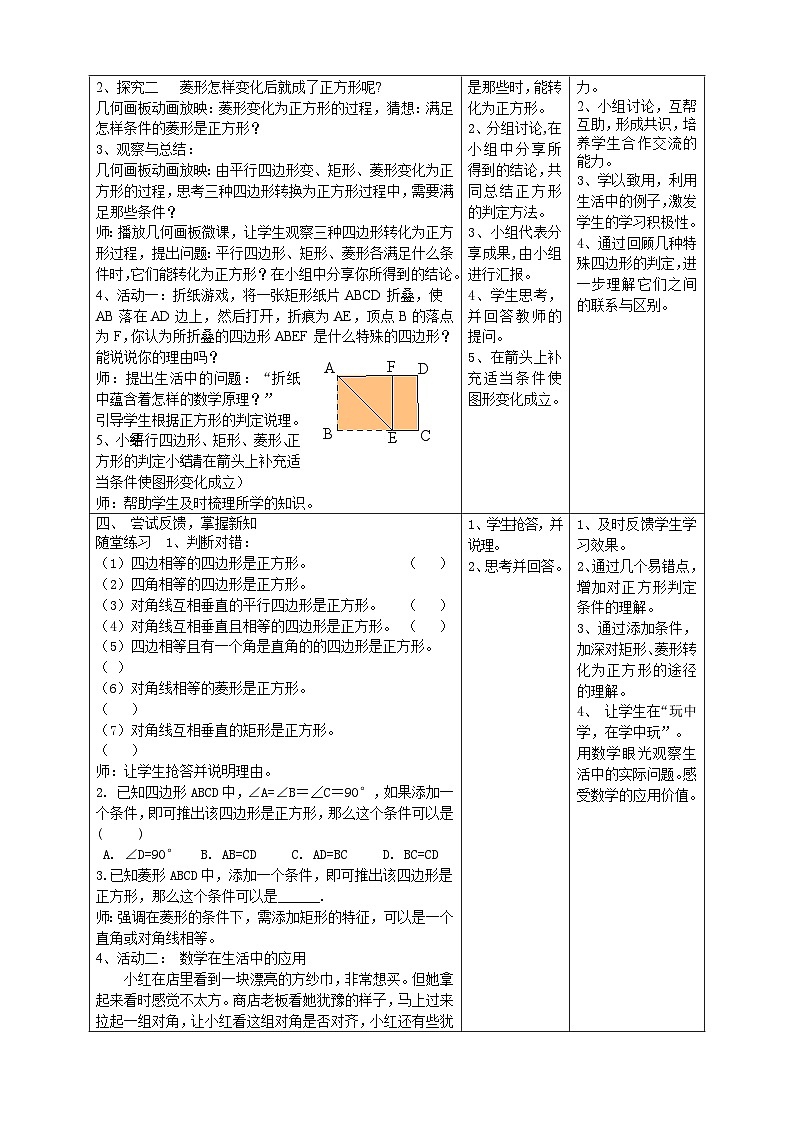
探究二 菱形怎样变化后就成了正方形呢?
几何画板动画放映：菱形变化为正方形的过程，猜想：满足怎样条件的菱形是正方形？
3、观察与总结：
几何画板动画放映：由平行四边形变、矩形、菱形变化为正方形的过程，思考三种四边形转换为正方形过程中，需要满足那些条件？
师：播放几何画板微课，让学生观察三种四边形转化为正方形过程，提出问题：平行四边形、矩形、菱形各满足什么条件时，它们能转化为正方形？在小组中分享你所得到的结论。
4、活动一：折纸游戏，将一张矩形纸片ABCD折叠，使
E图10
C图10
F图10
B图10
A
图10
D图10
AB落在AD边上，然后打开，折痕为AE，顶点B的落点为F，你认为所折叠的四边形ABEF是什么特殊的四边形？能说说你的理由吗？
师：提出生活中的问题：“折纸中蕴含着怎样的数学原理？”
引导学生根据正方形的判定说理。
5、小结：平行四边形、矩形、菱形、正方形的判定小结（请在箭头上补充适当条件使图形变化成立）
师：帮助学生及时梳理所学的知识。
1、认真观察三种变化过程，并思考三种图形各满足的条件是那些时，能转化为正方形。
2、分组讨论,在小组中分享所得到的结论，共同总结正方形的判定方法。
3、小组代表分享成果,由小组进行汇报。
4、学生思考，并回答教师的提问。
5、在箭头上补充适当条件使图形变化成立。
1、让学生进行总结，并归纳几何语言，培养学生观察与总结能力，独立思考的能力。
2、小组讨论，互帮互助，形成共识，培养学生合作交流的能力。
3、学以致用，利用生活中的例子，激发学生的学习积极性。
4、通过回顾几种特殊四边形的判定，进一步理解它们之间的联系与区别。
四、 尝试反馈，掌握新知
随堂练习 1、判断对错：
（1）四边相等的四边形是正方形。 （ ）
（2）四角相等的四边形是正方形。
（3）对角线互相垂直的平行四边形是正方形。 （ ）
（4）对角线互相垂直且相等的四边形是正方形。 （ ）
（5）四边相等且有一个角是直角的的四边形是正方形。（ ）
（6）对角线相等的菱形是正方形。 （ ）
（7）对角线互相垂直的矩形是正方形。 （ ）
师：让学生抢答并说明理由。
2. 已知四边形ABCD中，∠A=∠B＝∠C＝90°，如果添加一个条件，即可推出该四边形是正方形，那么这个条件可以是 ( )
A. ∠D=90° B. AB=CD C. AD=BC D. BC=CD
已知菱形ABCD中，添加一个条件，即可推出该四边形是正方形，那么这个条件可以是______.
师：强调在菱形的条件下，需添加矩形的特征，可以是一个直角或对角线相等。
4、活动二： 数学在生活中的应用
小红在店里看到一块漂亮的方纱巾，非常想买。但她拿起来看时感觉不太方。商店老板看她犹豫的样子，马上过来拉起一组对角，让小红看这组对角是否对齐，小红还有些犹豫，老板又拉起另一组对角，让小红检验。小红终于买了这块纱巾。你认为小红买的这块纱巾真是正方形吗？你能帮她检验吗？
师释疑：对折两次，能完全重合，说明四边相等，只能说明是菱形。
提问：怎样再检验一次，就能保证是正方形？
1、学生抢答，并说理。
2、思考并回答。
及时反馈学生学习效果。
通过几个易错点，增加对正方形判定条件的理解。
3、通过添加条件，加深对矩形、菱形转化为正方形的途径的理解。
4、 让学生在“玩中学，在学中玩”。
用数学眼光观察生活中的实际问题。感受数学的应用价值。
1
2
3
五、运用新知
1、例题讲解：
例：如图，点E，F，P，Q分别是正方形ABCD的四条边上的点，并且AP=BQ=CE=DF。
求证：四边形EFPQ是正方形.
师：分析证明思路，师生共同得出证明过程，并指出判定正方形的途径：先证菱形，再增加矩形的特征。
提出问题：有没有别的证法？再学生回答的基础上，指出可以先证三个直角得到矩形，然后证一组邻边相等，得到菱形的特征，从而证出是正方形。
在教师引导下，寻找证题思路，回答教师提出的问题，并思考别的证法。
例题既综合运用正方形的性质和判定，又用到全等三角形的性质和判定，以及菱形的判定，对训练学生的逻辑思维能力很有帮助。
六、 拓展提升
在△ABC中，点D、E、F分别在BC、AB、AC上，且DE∥AC, DF∥AB.
(1)如果∠BAC=90º，那么四边形AEDF是________形；
(2)如果AD是△BAC的角平分线，那么四边形AEDF是______形；
(3)如果∠BAC=90º，AD是△ABC的角平分线，
那么四边形AEDF是______形；
师：点评学生的回答，分析：平行四边形添加一个直角，得到矩形；平行四边形添加一组邻边相等，得到菱形；把两个条件综合起来，就得到正方形。
学生思考，练习。
学生代表讲证明思路。
1、通过逐步添加条件，理解平行四边形转化为矩形、菱形、以及正方形的方法，进一步认识这几种特殊四边形之间的关系。
2、培养学生分析问题、解决问题的能力
3、训练学生运用已有知识去解决新问题的能力。
七、 课堂总结，知识升华
1、学生回顾本节所学的知识；正方形有哪些判定方法？
2、学生从知识和思想方法两方面谈感悟与收获。
3、教师总结。
总结正方形判定的方法。
培养学生善于思考、归纳总结的习惯，学会总结与梳理知识的方法。
八、 分层布置作业
必做 课本98页 第12题 104页 第九题
选做 选做《同步学习》74页 第6题
学生根据自己的能力，选择相应层次的作业，独立完成。
让不同程度的学生得到不同的发展，体现分层教学的思想。
板书设计
19.3.3 正方形的判定
正方形的判定：
一、定义法：有一个角是直角且有一组邻边相等的平行四边形是正方形。
即：平行四边形+矩形特征+菱形特征=正方形
矩形+菱形特征=正方形
菱形+矩形特征=正方形
对角线法：两条对角线互相垂直平分且相等的四边形是正方形
练习：在△ABC中，点D、E、F分别在BC、AB、AC上，且DE∥AC,DF∥AB.
(1)如果∠BAC=90º，那么四边形AEDF是________形；
(2)如果AD是△BAC的角平分线，那么四边形AEDF是______形；
(3)如果∠BAC=90º，AD是△ABC的角平分线，
那么四边形AEDF是______形；
证明:∵DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形,
(1)∵∠BAC=90º,
∴平行四边形AEDF是矩形.
（2）∵AD是△ABC的角平分线,∴∠1=∠2,
而∠3=∠2，∴∠1=∠3，∴AE=DE
∴平行四边形AEDF是菱形。