初中数学第十七章 勾股定理17.1 勾股定理评课ppt课件

这是一份初中数学第十七章 勾股定理17.1 勾股定理评课ppt课件，共19页。PPT课件主要包含了学习目标，新课导入，概念剖析，想一想，方法一割，方法二补，方法三拼，SA+SBSC，勾股定理，SAa2等内容，欢迎下载使用。
1.经历探索勾股定理的过程,体会数形结合和从特殊到一般的思想.2.能掌握用面积法证明勾股定理,能利用勾股定理进行简单的计算
由于安全问题，工人小戴打算加一条钢索用来稳固电线杆.从电线杆离地面8m处向地面拉一条钢索，如果这条钢索在地面的固定点距离电线杆底部6m，那么工人小戴应准备多长的钢索？
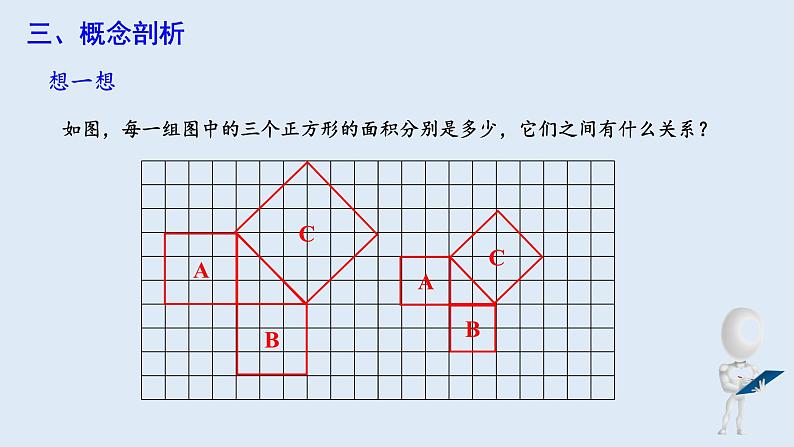
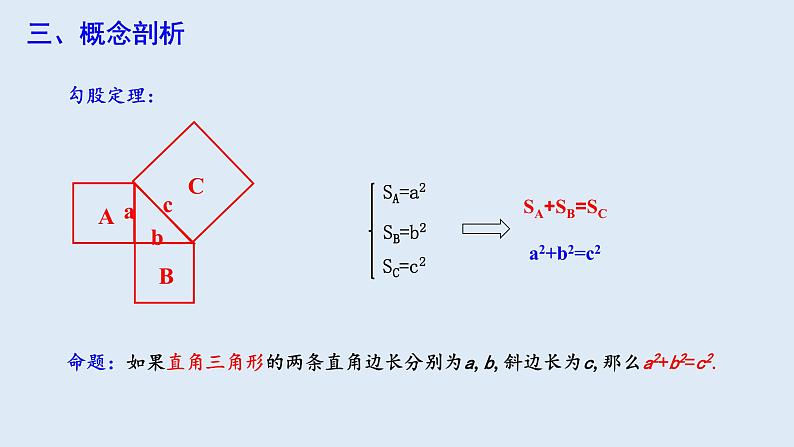
如图，每一组图中的三个正方形的面积分别是多少，它们之间有什么关系？
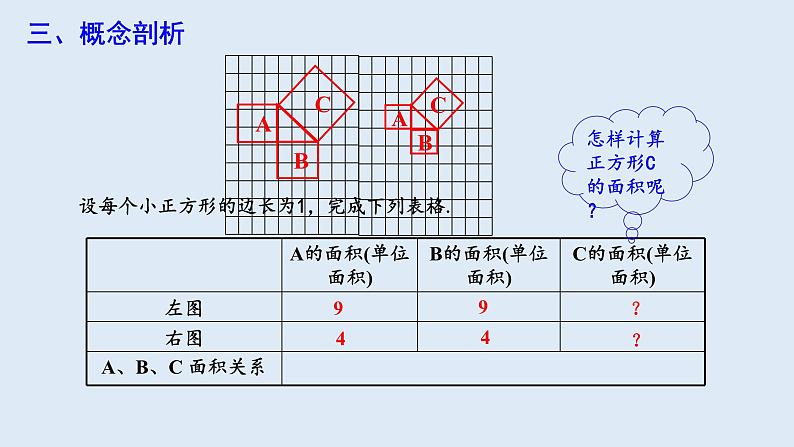
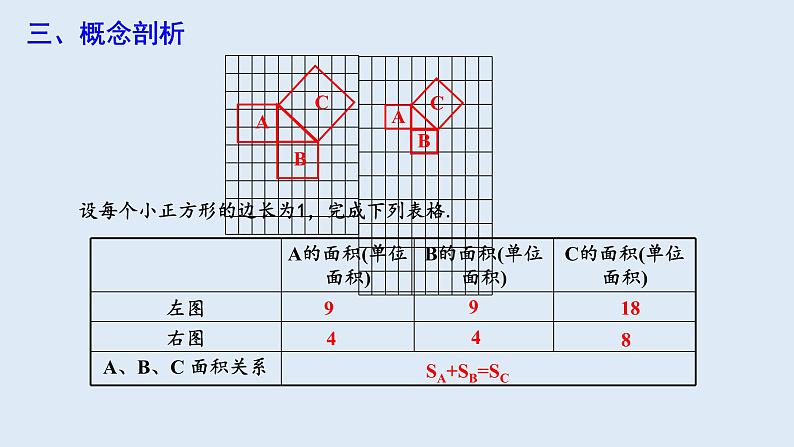
设每个小正方形的边长为1，完成下列表格.
怎样计算正方形C的面积呢？
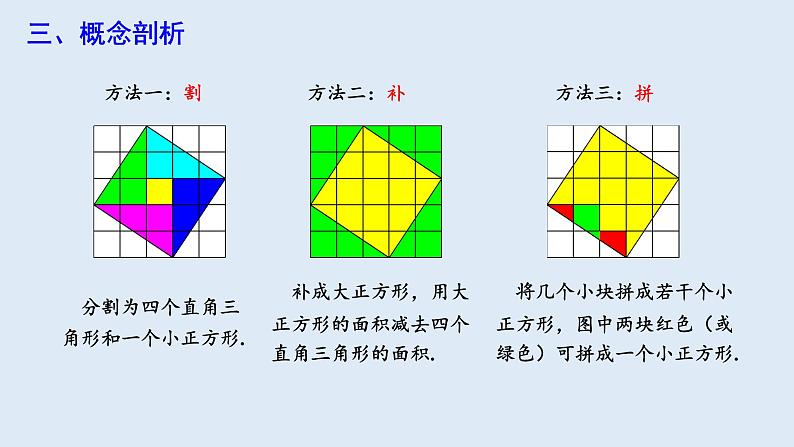
分割为四个直角三角形和一个小正方形.
补成大正方形，用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形，图中两块红色（或绿色）可拼成一个小正方形.
命题：如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么a2+b2=c2.
例1.求图中直角三角形的未知边的长度.
解：在Rt△ABC中，∠B=900 ，AB=8，BC=6.
根据勾股定理可得：
AC2=AB2+BC2=82+62=100
∴AC=10
例2.如图，每个小正方形的边长为1，a,b,c是△ABC的三边，求△ABC的周长．
勾股定理反映了直角三角形中边的数量关系，所以在直角三角形中已知任意两边长，使用勾股定理求第三边长. 
1.在△ABC中，∠C=90°，a、b、c分别为∠A、∠B、∠C的对边．（1）如果a=5，b=12，那么c= ．（2）如果c=61，a=60，那么b= ．（3）若∠A=45°，a=2，则c= ．
2.求斜边长为17 cm、一条直角边长为15 cm的直角三角形的面积.
解：设另一条直角边长是x cm，由勾股定理得:
故直角三角形的面积是:
所以另一直角边长为8 cm，
152+ x2 =172，x2=172-152=289–225=64，
解得 x=±8（负值舍去），
例3.[定理表述]请你根据图1中的直角三角形，写出勾股定理内容；[尝试证明]以图1中的直角三角形为基础，可以构造出以a、b为底，以a+b为高的直角梯形（如图2），请你利用图2，验证勾股定理．
定理表述：直角三角形中，两直角边的平方和等于斜边的平方．
证明：∵SABCD=S△ABE+S△AED+S△CDE，
∴（a+b）2=2ab+c2，
∴a2+2ab+b2=2ab+c2，
勾股定理的证明，一般都是通过用不同的方式表示同一图形的面积，即等面积法得证.
3.学完了勾股定理后，张老师给同学们布置了这样一道题：有两个形状、大小完全相同的香烟盒按照图1放置，从正前方看图1得到的图形如图2所示，你能运用这个图形证明勾股定理吗？赶紧试一试吧，相信你一定能行！（提示：连接AC、CF、AF）
证明：连接AC、CF、AF．
两者列成等式化简即可得：a2+c2=b2．