2023-2024学年甘肃省天水市秦安县兴国初级中学七年级（上）期末数学试卷（含解析）

这是一份2023-2024学年甘肃省天水市秦安县兴国初级中学七年级（上）期末数学试卷（含解析），共21页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
1．2的相反数和绝对值分别是（ ）
A．2，2B．﹣2，2C．﹣2，﹣2D．2，﹣2
2．未来三年，国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题．将8450亿元用科学记数法表示为（ ）
A．0.845×1012元B．8.45×1011元
C．8.45×1012元D．84.5×1010元
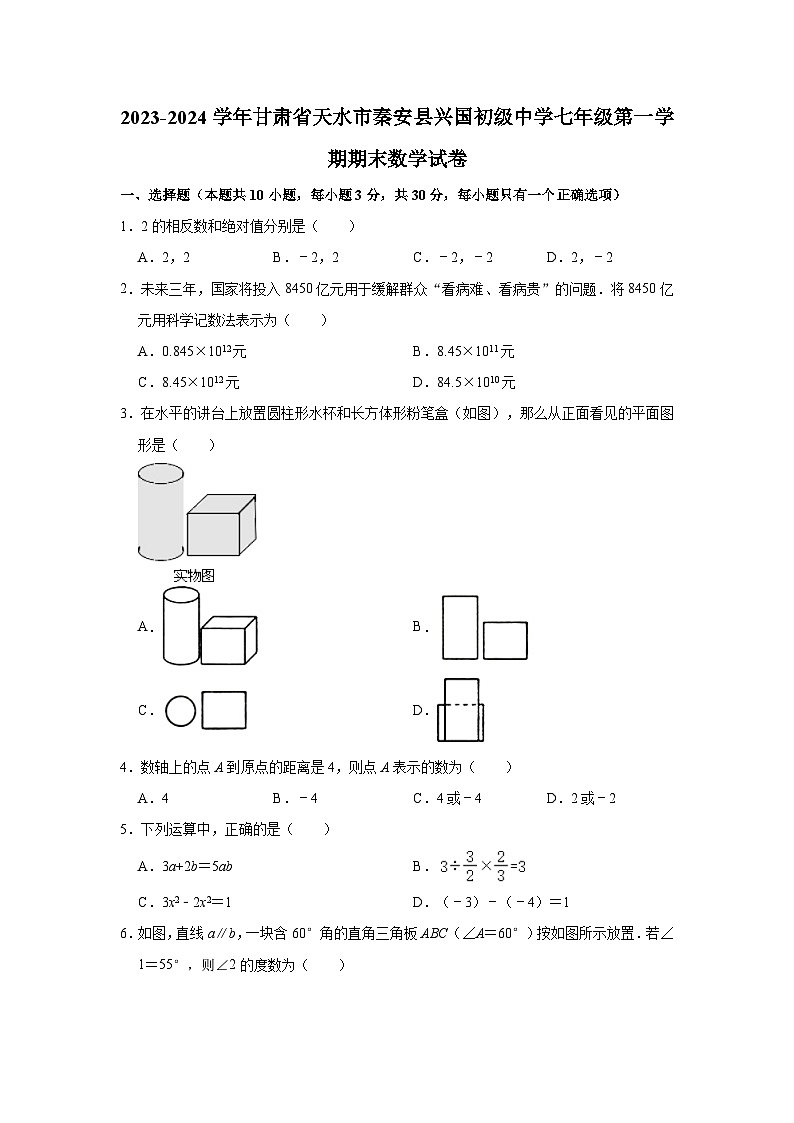
3．在水平的讲台上放置圆柱形水杯和长方体形粉笔盒（如图），那么从正面看见的平面图形是（ ）
A．B．
C．D．
4．数轴上的点A到原点的距离是4，则点A表示的数为（ ）
A．4B．﹣4C．4或﹣4D．2或﹣2
5．下列运算中，正确的是（ ）
A．3a+2b＝5abB．
C．3x2﹣2x2＝1D．（﹣3）﹣（﹣4）＝1
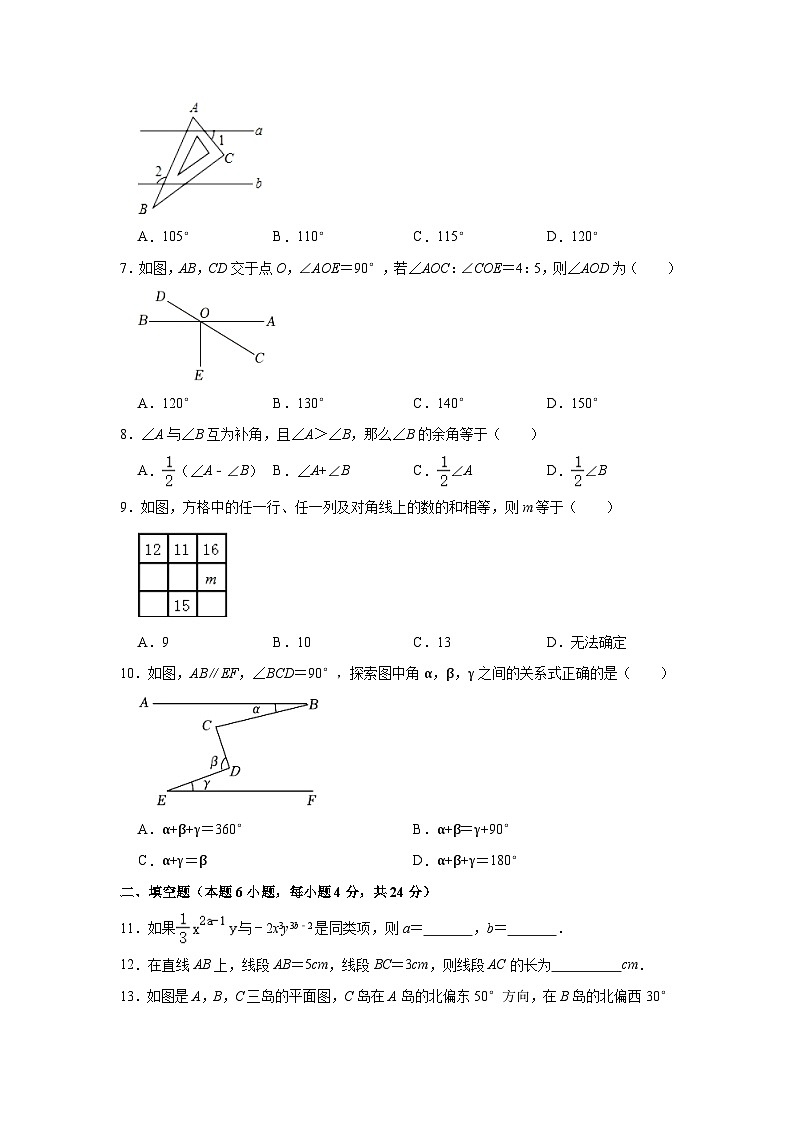
6．如图，直线a∥b，一块含60°角的直角三角板ABC（∠A＝60°）按如图所示放置．若∠1＝55°，则∠2的度数为（ ）
A．105°B．110°C．115°D．120°
7．如图，AB，CD交于点O，∠AOE＝90°，若∠AOC：∠COE＝4：5，则∠AOD为（ ）
A．120°B．130°C．140°D．150°
8．∠A与∠B互为补角，且∠A＞∠B，那么∠B的余角等于（ ）
A．（∠A﹣∠B）B．∠A+∠BC．∠AD．∠B
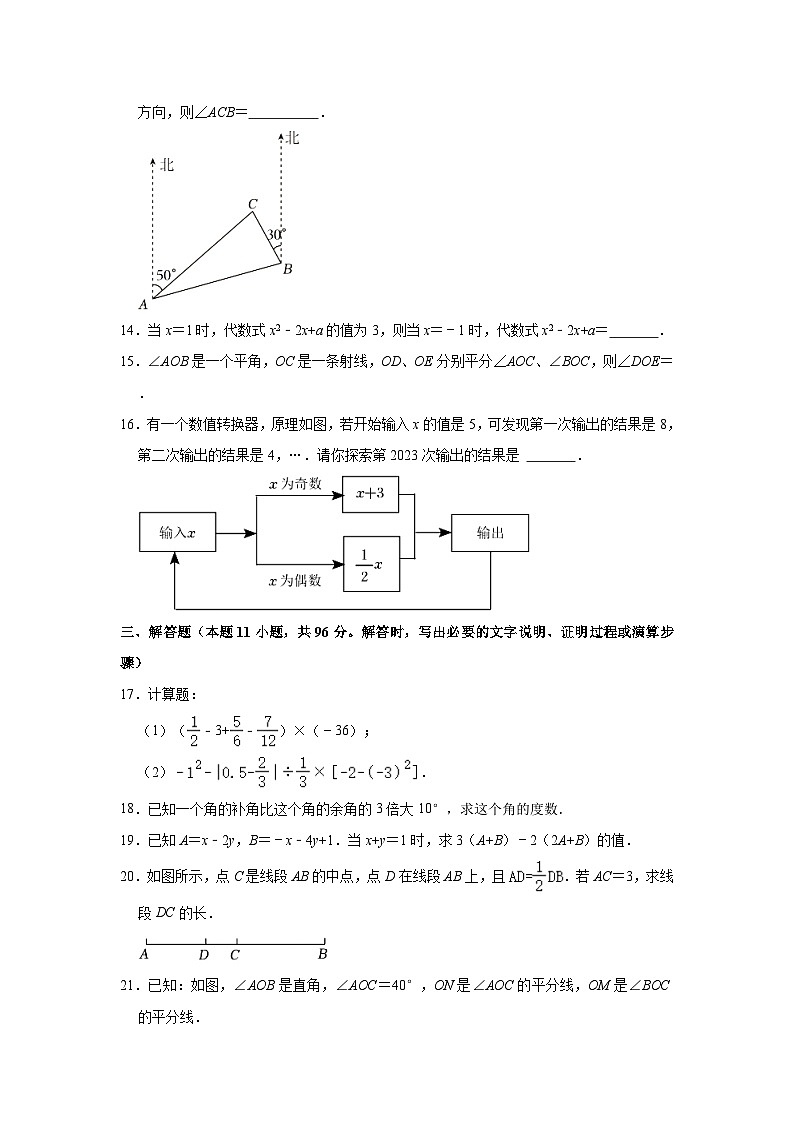
9．如图，方格中的任一行、任一列及对角线上的数的和相等，则m等于（ ）
A．9B．10C．13D．无法确定
10．如图，AB∥EF，∠BCD＝90°，探索图中角α，β，γ之间的关系式正确的是（ ）
A．α+β+γ＝360°B．α+β＝γ+90°
C．α+γ＝βD．α+β+γ＝180°
二、填空题（本题6小题，每小题4分，共24分）
11．如果与﹣2x3y3b﹣2是同类项，则a＝ ，b＝ ．
12．在直线AB上，线段AB＝5cm，线段BC＝3cm，则线段AC的长为 cm．
13．如图是A，B，C三岛的平面图，C岛在A岛的北偏东50°方向，在B岛的北偏西30°方向，则∠ACB＝ ．
14．当x＝1时，代数式x2﹣2x+a的值为3，则当x＝﹣1时，代数式x2﹣2x+a＝ ．
15．∠AOB是一个平角，OC是一条射线，OD、OE分别平分∠AOC、∠BOC，则∠DOE＝ ．
16．有一个数值转换器，原理如图，若开始输入x的值是5，可发现第一次输出的结果是8，第二次输出的结果是4，…．请你探索第2023次输出的结果是 ．
三、解答题（本题11小题，共96分。解答时，写出必要的文字说明、证明过程或演算步骤）
17．计算题：
（1）（﹣3+﹣）×（﹣36）；
（2）．
18．已知一个角的补角比这个角的余角的3倍大10°，求这个角的度数．
19．已知A＝x﹣2y，B＝﹣x﹣4y+1．当x+y＝1时，求3（A+B）﹣2（2A+B）的值．
20．如图所示，点C是线段AB的中点，点D在线段AB上，且．若AC＝3，求线段DC的长．
21．已知：如图，∠AOB是直角，∠AOC＝40°，ON是∠AOC的平分线，OM是∠BOC的平分线．
（1）求∠MON的大小；
（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？为什么？
22．已知代数式A＝2x2+3xy+2y﹣1，B＝x2﹣xy+x﹣
（1）当x＝y＝﹣2时，求A﹣2B的值；
（2）若A﹣2B的值与x的取值无关，求y的值．
23．已知∠1和∠2（∠1＞∠2），利用直尺和圆规作一个角使它等于∠1﹣∠2．（不写画法，只保留作图痕迹）
24．新华书店推出售书优惠方案：一次性购书不超过100 元，不享受优惠；一次性购书超过100元但不超过200元一律打九折；一次性购书200元以上一律打八折．
（1）如果小明一次性购书的原价为250元，那么他实际付款 元；
（2）如果小华同学一次性购书付款162元，那么小华所购书的原价为多少元？
25．有理数a、b、c在数轴上的对应点分别为A，B，C，其位置如图所示，试去掉绝对值符号并合并同类项：|c|﹣|c+b|+|a﹣c|+|b+a|．
26．已知如图，∠DAE＝∠E，∠B＝∠D，直线AD与BE平行吗？直线AB与DC平行吗？说明理由（请在下面的解答过程的空格内填空或在括号内填写理由）．
解：直线AD与BE平行，直线AB与DC平行．
理由如下：
∵∠DAE＝∠E（已知）
∴ ∥
∴∠D＝∠DCE
又∵∠B＝∠D
∴∠B＝∠ （等量代换）
∴ ∥ ．
27．如图，P是线段AB上任一点，AB＝12cm，C、D两点分别从P、B同时向A点运动，且C点的运动速度为2cm/s，D点的运动速度为3cm/s，运动的时间为t s．
（1）若AP＝8cm，
①运动1s后，求CD的长；
②当D在线段PB上运动时，试说明AC＝2CD；
（2）如果t＝2s时，CD＝1cm，试探索AP的值．
参考答案
一、选择题（本题共10小题，每小题3分，共30分，每小题只有一个正确选项）
1．2的相反数和绝对值分别是（ ）
A．2，2B．﹣2，2C．﹣2，﹣2D．2，﹣2
【分析】根据相反数和绝对值的定义求解即可．
解：2的相反数是﹣2，绝对值是2，
故选：B．
【点评】本题考查了相反数和绝对值的定义，绝对值规律总结：一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；0的绝对值是0．
相反数规律方法总结：求一个数的相反数的方法就是在这个数的前边添加“﹣”，如a的相反数是﹣a，m+n的相反数是﹣（m+n），这时m+n是一个整体，在整体前面添负号时，要用小括号．
2．未来三年，国家将投入8450亿元用于缓解群众“看病难、看病贵”的问题．将8450亿元用科学记数法表示为（ ）
A．0.845×1012元B．8.45×1011元
C．8.45×1012元D．84.5×1010元
【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值≥10时，n是正数；当原数的绝对值＜1时，n是负数．
解：8450亿元用科学记数法表示为8.45×1011，
故选：B．
【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．
3．在水平的讲台上放置圆柱形水杯和长方体形粉笔盒（如图），那么从正面看见的平面图形是（ ）
A．B．
C．D．
【分析】先细心观察原立体图形中圆柱和正方体的位置关系，找到从正面看所得到的图形即可．
解：圆柱的主视图是矩形，正方体的主视图是正方形，所以它们的主视图是图B．
故选：B．
【点评】此题主要考查了三视图的知识，主视图是从物体的正面看得到的视图．
4．数轴上的点A到原点的距离是4，则点A表示的数为（ ）
A．4B．﹣4C．4或﹣4D．2或﹣2
【分析】在数轴上点A到原点的距离为4的数有两个，意义相反，互为相反数．即4和﹣4．
解：在数轴上，4和﹣4到原点的距离为4．
∴点A所表示的数是4和﹣4．
故选：C．
【点评】此题考查的知识点是数轴．关键是要明确原点的距离为4的数有两个，意义相反．
5．下列运算中，正确的是（ ）
A．3a+2b＝5abB．
C．3x2﹣2x2＝1D．（﹣3）﹣（﹣4）＝1
【分析】同类项要合并，系数相加字母和字母的指数不变，按运算顺序计算即可．
解：A、3a+2b＝5ab，不是同类项，不能合并，故本选项错误；
B、原式＝，故本选项错误；
C、3x2﹣2x2＝x2，故本选项错误；
D、（﹣3）﹣（﹣4）＝1，故本选项正确．
故选：D．
【点评】本题考查了有理数的混合运算、同类项和合并同类项的法则，是基础知识比较简单．
6．如图，直线a∥b，一块含60°角的直角三角板ABC（∠A＝60°）按如图所示放置．若∠1＝55°，则∠2的度数为（ ）
A．105°B．110°C．115°D．120°
【分析】如图，首先证明∠AMO＝∠2；然后运用对顶角的性质求出∠ANM＝55°，借助三角形外角的性质求出∠AMO即可解决问题．
解：如图，∵直线a∥b，
∴∠AMO＝∠2；
∵∠ANM＝∠1，而∠1＝55°，
∴∠ANM＝55°，
∴∠AMO＝∠A+∠ANM＝60°+55°＝115°，
∴∠2＝∠AMO＝115°．
故选：C．
【点评】该题主要考查了平行线的性质、对顶角的性质、三角形的外角性质等几何知识点及其应用问题；牢固掌握平行线的性质、对顶角的性质等几何知识点是灵活运用、解题的基础．
7．如图，AB，CD交于点O，∠AOE＝90°，若∠AOC：∠COE＝4：5，则∠AOD为（ ）
A．120°B．130°C．140°D．150°
【分析】根据图形中角的比例关系以及邻补角的定义进行计算即可．
解：∵∠AOE＝90°＝∠AOC+∠COE，而∠AOC：∠COE＝4：5，
∴∠AOC＝90°×＝40°，
∴∠AOE＝180°﹣40°＝140°．
故选：C．
【点评】本题考查对顶角、邻补角，掌握对顶角相等以及邻补角的定义是正确解答的关键．
8．∠A与∠B互为补角，且∠A＞∠B，那么∠B的余角等于（ ）
A．（∠A﹣∠B）B．∠A+∠BC．∠AD．∠B
【分析】根据互为补角的两个角的和等于180°用∠A表示出∠B，再根据互为余角的两个角的和等于90°表示出∠B的余角即可得解．
解：∵∠A与∠B互为补角，
∴∠B＝180°﹣∠A，
∴∠B的余角＝90°﹣（180°﹣∠A）＝∠A﹣90°＝∠A﹣（∠A+∠B）＝（∠A﹣∠B）．
故选：A．
【点评】本题考查了余角和补角，熟记概念是解题的关键．注意：余角（补角）与这两个角的位置没有关系．不论这两个角在哪儿，只要度数之和满足了定义，则它们就具备相应的关系．
9．如图，方格中的任一行、任一列及对角线上的数的和相等，则m等于（ ）
A．9B．10C．13D．无法确定
【分析】由第一行可得每一行的和为39，继而可求出m左边及m下面的数，即能得出m的值．
解：由题意得三个数的和为39，
∴m左边的空格里面的数为13，m下面的空格里面的数为14．
∴m的值为39﹣16﹣14＝9．
故选：A．
【点评】本题考查有理数的加法，难度不大，求出m下面的空格里面的数是关键．
10．如图，AB∥EF，∠BCD＝90°，探索图中角α，β，γ之间的关系式正确的是（ ）
A．α+β+γ＝360°B．α+β＝γ+90°
C．α+γ＝βD．α+β+γ＝180°
【分析】首先过点C作CM∥AB，过点D作DN∥AB，由AB∥EF，即可得AB∥CM∥DN∥EF，然后由两直线平行，内错角相等，即可求得答案．
解：过点C作CM∥AB，过点D作DN∥AB，
∵AB∥EF，
∴AB∥CM∥DN∥EF，
∴∠BCM＝α，∠DCM＝∠CDN，∠EDN＝γ，
∵β＝∠CDN+∠EDN＝∠CDN+γ①，∠BCD＝α+∠CDN＝90°②，
由①②得：α+β﹣γ＝90°．
故选：B．
【点评】此题考查了平行线的性质．此题难度适中，注意掌握辅助线的作法，注意数形结合思想的应用．
二、填空题（本题6小题，每小题4分，共24分）
11．如果与﹣2x3y3b﹣2是同类项，则a＝ 2 ，b＝ 1 ．
【分析】所含字母相同，并且相同字母的指数也相同的项叫做同类项，由此得到2a﹣1＝3，3b﹣2＝1，求出a、b的值即可．
解：如果与﹣2x3y3b﹣2是同类项，
则2a﹣1＝3，3b﹣2＝1，
解得a＝2，b＝1，
故答案为：2，1．
【点评】本题考查了同类项，解一元一次方程，熟知同类项的定义是解题的关键．
12．在直线AB上，线段AB＝5cm，线段BC＝3cm，则线段AC的长为 2或8 cm．
【分析】分当C在线段AB上和当C在线段AB的延长线上两种情况进行讨论即可求解．
解：当C在线段AB上时，AC＝AB﹣BC＝5﹣3＝2cm；
当C在线段AB的延长线上时：AC＝AB+BC＝5+3＝8cm．
故答案为：2或8．
【点评】本题考查了选段的计算，注意到分情况进行讨论是关键．
13．如图是A，B，C三岛的平面图，C岛在A岛的北偏东50°方向，在B岛的北偏西30°方向，则∠ACB＝ 80° ．
【分析】根据方位角的概念，过点C作辅助线，构造两组平行线，利用平行线的性质即可求解．
解：如图，作CE∥AD，
∵DA∥FB，
∴CE∥BF．
∵CE∥AD，
∴∠DAC＝∠ACE＝50°．
∵CE∥BF，
∴∠CBF＝∠BCE＝30°．
∴∠ACB＝∠ACE+∠BCE＝50°+30°＝80°．
故答案为：80°．
【点评】本题考查了方位角的概念，解答题目的关键是作辅助线，构造平行线．两直线平行，内错角相等．
14．当x＝1时，代数式x2﹣2x+a的值为3，则当x＝﹣1时，代数式x2﹣2x+a＝ 7 ．
【分析】将x＝1代入代数式求出a的值，将x＝﹣1及a的值代入计算即可求出值．
解：∵当x＝1时，x2﹣2x+a＝3，
∴1﹣2+a＝3，即a＝4，
∴当x＝﹣1时，x2﹣2x+a＝（﹣1）2﹣2×（﹣1）+4＝7．
故答案为：7．
【点评】此题考查了代数式求值，求出a的值是解本题的关键．
15．∠AOB是一个平角，OC是一条射线，OD、OE分别平分∠AOC、∠BOC，则∠DOE＝ 90° ．
【分析】根据角平分线定义得到∠DOC＝∠AOC，∠EOC＝∠BOC，把它们相加得到∠DOE＝∠AOB，然后根据平角的定义进行计算．
解：∵OD、OE分别平分∠AOC、∠BOC，
∴∠DOC＝∠AOC，∠EOC＝∠BOC，
∴∠DOC+∠EOC＝（∠AOC+∠BOC），
∴∠DOE＝∠AOB＝×180°＝90°．
故答案为90°．
【点评】本题考查了角平分线的定义：从一个角的顶点出发，把这个角分成相等的两个角的射线叫做这个角的平分线．
16．有一个数值转换器，原理如图，若开始输入x的值是5，可发现第一次输出的结果是8，第二次输出的结果是4，…．请你探索第2023次输出的结果是 1 ．
【分析】根据题意，可以写出前几个输出结果，从而可以发现输出结果的变化特点，从而可以求得第2023次输出的结果．
解：第一次输出：5+3＝8，
第二次输出：，
第三次输出：，
第四次输出：，
第五次输出：1+3＝4，
第六次输出：，
……，
从第二次开始，每3次为一循环，按照4，2，1的顺序进行循环，
∵（2023﹣1）÷3＝674，
∴第2023次输出的结果是第674组的第3个数，
∴第2023次输出的结果是1，
故答案为：1．
【点评】本题考查数字的变化类，流程图，有理数的混合运算，熟练掌握找规律是关键．
三、解答题（本题11小题，共96分。解答时，写出必要的文字说明、证明过程或演算步骤）
17．计算题：
（1）（﹣3+﹣）×（﹣36）；
（2）．
【分析】（1）根据乘法分配律进行计算即可；
（2）先乘方再计算括号内部分，最后乘除加减即可．
解：（1）原式＝（﹣+﹣）×（﹣36）
＝（﹣36）×（﹣）+（﹣36）×﹣（﹣36）×
＝90﹣30+21
＝81；
（2）
＝﹣1﹣×3×（﹣2﹣9）
＝﹣1﹣×3×（﹣11）
＝﹣1+
＝．
【点评】本题考查了有理数的混合运算，熟练掌握相关运算法则是关键．
18．已知一个角的补角比这个角的余角的3倍大10°，求这个角的度数．
【分析】利用题中“一个角的补角比这个角的余角的3倍大10°”作为相等关系列方程求解即可．
解：设这个角是x，则（180°﹣x）﹣3（90°﹣x）＝10°，
解得x＝50°．
故答案为50°．
【点评】主要考查了余角和补角的概念以及运用．互为余角的两角的和为90°，互为补角的两角之和为180度．解此题的关键是能准确的从图中找出角之间的数量关系，从而计算出结果．
19．已知A＝x﹣2y，B＝﹣x﹣4y+1．当x+y＝1时，求3（A+B）﹣2（2A+B）的值．
【分析】将3（A+B）﹣2（2A+B）去括号合并同类项化简后将A，B两整式代入后化简为含有x+y的系形式，再将x+y＝1代入计算可求解．
解：∵A＝x﹣2y，B＝﹣x﹣4y+1，
∴3（A+B）﹣2（2A+B）
＝3A+3B﹣4A﹣2B
＝B﹣A
＝（﹣x﹣4y+1）﹣（x﹣2y）
＝﹣x﹣4y+1﹣x+2y
＝﹣2x﹣2y+1
＝﹣2（x+y）+1，
∵x+y＝1，
∴原式＝﹣2×1+1＝﹣1．
【点评】本题主要考查整式的化简求值，灵活运用去括号．合并同类项化简是解题的关键．
20．如图所示，点C是线段AB的中点，点D在线段AB上，且．若AC＝3，求线段DC的长．
【分析】利用AC＝3，C是线段AB的中点，可以求出AB的长，再利用，可以求出AD，DB的长，最后利用线段的和差公式求出DC的长即可．
解：∵AC＝3，C是线段AB的中点，
∴AB＝2AC＝2×3＝6，
∵，AB＝AD+BD，
∴，
∴DC＝AC﹣AD＝3﹣2＝1．
【点评】本题主要考查两点间的距离，熟练掌握中点的定义和线段的和差关系是解题的关键．
21．已知：如图，∠AOB是直角，∠AOC＝40°，ON是∠AOC的平分线，OM是∠BOC的平分线．
（1）求∠MON的大小；
（2）当锐角∠AOC的大小发生改变时，∠MON的大小是否发生改变？为什么？
【分析】（1）根据∠AOB是直角，∠AOC＝40°，可得∠AOB+∠AOC＝90°+40°＝130°，再利用OM是∠BOC的平分线，ON是∠AOC的平分线，即可求得答案．
（2）根据∠MON＝∠MOC﹣∠NOC，又利用∠AOB是直角，不改变，可得．
解：（1）∵∠AOB是直角，∠AOC＝40°，
∴∠AOB+∠AOC＝90°+40°＝130°，
∵OM是∠BOC的平分线，ON是∠AOC的平分线，
∴，．
∴∠MON＝∠MOC﹣∠NOC＝65°﹣20°＝45°，
（2）当锐角∠AOC的大小发生改变时，∠MON的大小不发生改变．
∵＝，
又∠AOB是直角，不改变，
∴．
【点评】此题主要考查角的计算和角平分线的定义等知识点的理解和掌握，难度不大，属于基础题．
22．已知代数式A＝2x2+3xy+2y﹣1，B＝x2﹣xy+x﹣
（1）当x＝y＝﹣2时，求A﹣2B的值；
（2）若A﹣2B的值与x的取值无关，求y的值．
【分析】（1）将A、B表示的代数式代入A﹣2B中，去括号，合并同类项即可；
（2）由（1）可知A﹣2B＝5xy+2y﹣2x，将含x的项合并得（5y﹣2）x+2y，令含xd的项系数为0即可．
解：（1）A﹣2B＝2x2+3xy+2y﹣1﹣2（）
＝2x2+3xy+2y﹣1﹣2x2+2xy﹣2x+1
＝5xy+2y﹣2x，
当x＝y＝﹣2时，
A﹣2B＝5xy+2y﹣2x
＝5×（﹣2）×（﹣2）+2×（﹣2）﹣2×（﹣2）
＝20；
（2）由（1）可知A﹣2B＝5xy+2y﹣2x＝（5y﹣2）x+2y，
若A﹣2B的值与x的取值无关，则5y﹣2＝0，
解得．
【点评】本题考查了整式的化简．整式的加减运算实际上就是去括号、合并同类项，这是各地中考的常考点．
23．已知∠1和∠2（∠1＞∠2），利用直尺和圆规作一个角使它等于∠1﹣∠2．（不写画法，只保留作图痕迹）
【分析】作∠AOB＝∠1，在∠AOB内部作∠BOC＝∠2，∠AOC即为所求．
解：作∠AOB＝∠1，在∠AOB内部作∠BOC＝∠2，如图：
∠AOC即为所求．
【点评】本题考查作图﹣复杂作图，解题的关键是熟练掌握作一个角等于已知角的尺规作图方法，属于中考常考题型．
24．新华书店推出售书优惠方案：一次性购书不超过100 元，不享受优惠；一次性购书超过100元但不超过200元一律打九折；一次性购书200元以上一律打八折．
（1）如果小明一次性购书的原价为250元，那么他实际付款 200 元；
（2）如果小华同学一次性购书付款162元，那么小华所购书的原价为多少元？
【分析】（1）根据一次性购书超过200元，打八折，可得出实际付款；
（2）设原价为x，则分两种情况讨论，①100＜x≤200，②x＞200，列出方程，解出后判断即可．
解：（1）实际付款＝250×0.8＝200元．
（2）设原价为x元，
①若100＜x≤200，则0.9x＝162，
解得：x＝180；
②若x＞200，则0.8x＝162，
解得：x＝202.5．
答：如果小华同学一次性购书付款162元，那么小华所购书的原价为180元或202.5元．
【点评】本题考查了一元一次方程的应用，解答本题的关键是理解打折的含义，第二问注意分类讨论．
25．有理数a、b、c在数轴上的对应点分别为A，B，C，其位置如图所示，试去掉绝对值符号并合并同类项：|c|﹣|c+b|+|a﹣c|+|b+a|．
【分析】先根据数轴上各点的位置判断出a、b、c的大小，判断出b+c、a﹣c、a+b的符号，再由绝对值的性质把原式进行化简即可．
解：由图知：b＜c＜0＜a，且|b|＞|a|，
∴c+b＜0，a﹣c＞0，b+a＜0，
∴原式＝﹣c﹣（﹣b﹣c）+（a﹣c）+（﹣b﹣a）
＝﹣c+b+c+a﹣c﹣b﹣a
＝﹣c．
【点评】本题考查的是整式的加减及数轴上的特点，熟知整式的加减实质上就是合并同类项是解答此题的关键．
26．已知如图，∠DAE＝∠E，∠B＝∠D，直线AD与BE平行吗？直线AB与DC平行吗？说明理由（请在下面的解答过程的空格内填空或在括号内填写理由）．
解：直线AD与BE平行，直线AB与DC平行．
理由如下：
∵∠DAE＝∠E（已知）
∴ AD ∥ BE
∴∠D＝∠DCE （两条直线平行，内错角相等）
又∵∠B＝∠D （已知）
∴∠B＝∠ DCE （等量代换）
∴ AB ∥ DC ．
【分析】因为∠DAE＝∠E，所以根据内错角相等，两条直线平行，可以证明AD∥BE；根据平行线的性质，可得∠D＝∠DCE，结合已知条件，运用等量代换，可得∠B＝∠DCE，可证明AB∥DC．
解：直线AD与BE平行，直线AB与DC平行．
理由如下：
∵∠DAE＝∠E，（已知）
∴AD∥BE，
∴∠D＝∠DCE．（两条直线平行，内错角相等）
又∵∠B＝∠D，（已知）
∴∠B＝∠DCE，（等量代换）
∴AB∥DC．
故答案为：AD，BE，（两条直线平行，内错角相等），（已知），DCE，AB，DC．
【点评】此题综合运用了平行线的性质和判定，关键是找准两条直线被第三条直线所截而形成的同位角、内错角．
27．如图，P是线段AB上任一点，AB＝12cm，C、D两点分别从P、B同时向A点运动，且C点的运动速度为2cm/s，D点的运动速度为3cm/s，运动的时间为t s．
（1）若AP＝8cm，
①运动1s后，求CD的长；
②当D在线段PB上运动时，试说明AC＝2CD；
（2）如果t＝2s时，CD＝1cm，试探索AP的值．
【分析】（1）①先求出PB、CP与DB的长度，然后利用CD＝CP+PB﹣DB即可求出答案；
②用t表示出AC、DP、CD的长度即可求证AC＝2CD；
（2）当t＝2时，求出CP、DB的长度，由于没有说明D点在C点的左边还是右边，故需要分情况讨论．
解：（1）①由题意可知：CP＝2×1＝2cm，DB＝3×1＝3cm，
∵AP＝8cm，AB＝12cm，
∴PB＝AB﹣AP＝4cm，
∴CD＝CP+PB﹣DB＝2+4﹣3＝3cm；
②∵AP＝8cm，AB＝12cm，
∴BP＝4cm，AC＝（8﹣2t）cm，
∴DP＝（4﹣3t）cm，
∴CD＝DP+CP＝2t+4﹣3t＝（4﹣t）cm，
∴AC＝2CD；
（2）当t＝2s时，
CP＝2×2＝4cm，DB＝3×2＝6cm，
当点D在C的右边时，如图所示：
由于CD＝1cm，
∴CB＝CD+DB＝7cm，
∴AC＝AB﹣CB＝5cm，
∴AP＝AC+CP＝9cm，
当点D在C的左边时，如图所示：
∴AD＝AB﹣DB＝6cm，
∴AP＝AD+CD+CP＝11cm，
综上所述，AP＝9cm或11cm．
【点评】本题考查两点间的距离，涉及列代数式，注意分类讨论是解题关键．