
2023-2024学年河南省南阳市油田八年级(上)期末数学试卷(含解析)
展开
这是一份2023-2024学年河南省南阳市油田八年级(上)期末数学试卷(含解析),共24页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。
1.下列各数为无理数的是( )
A.0.618B.C.D.
2.下列计算正确的是( )
A.(﹣3x)2=﹣9x2
B.7x+5x=12x2
C.(x﹣3)2=x2﹣6x+9
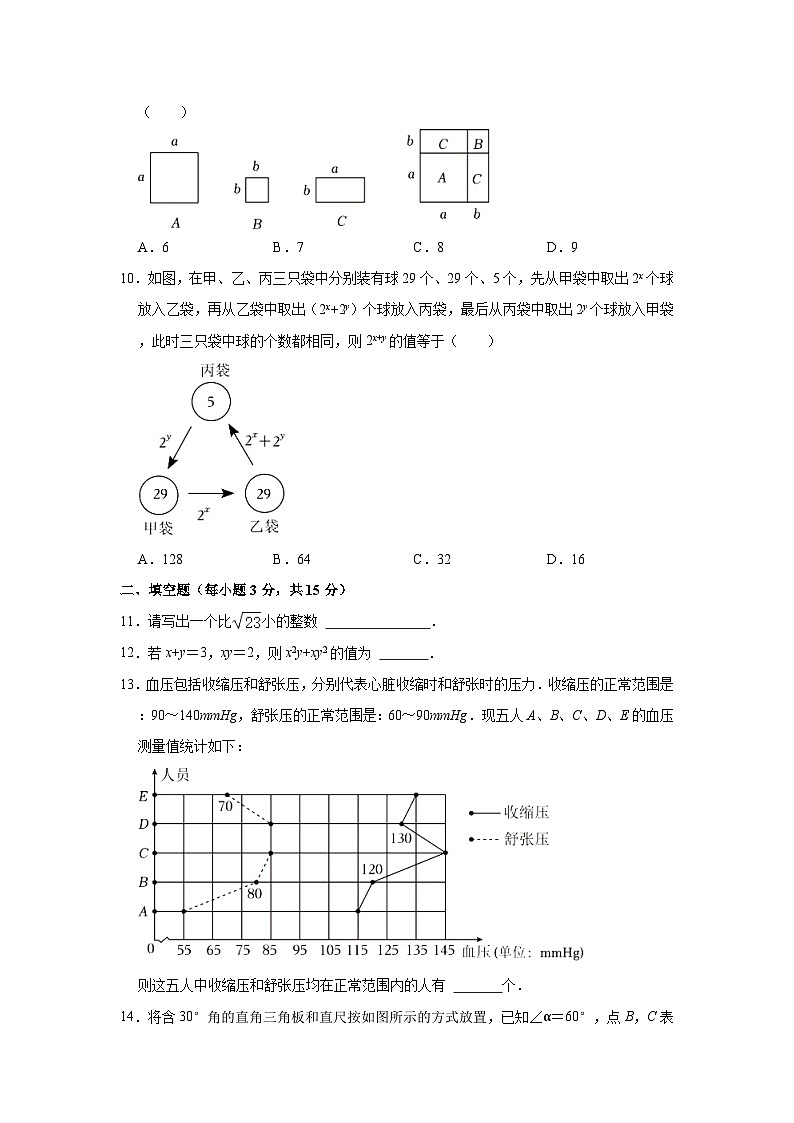
D.(x﹣2y)(x+2y)=x2+4y2
3.下列各式从左到右的变形,因式分解正确的是( )
A.(a+3)2=a2+6a+9
B.a2﹣4a+4=a(a﹣4)+4
C.5ax2﹣5ay2=5a(x+y)(x﹣y)
D.a2﹣2a﹣8=(a﹣2)(a+4)
4.如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA′、BB'的中点.只要量出A′B′的长度.就可以知道该零件内径AB的长度.依据的数学基本事实是( )
A.两角和它们的夹边分别相等的两个三角形全等
B.两边和它们的夹角分别相等的两个三角形全等
C.三边分别相等的两个三角形全等
D.两点之间线段最短
5.若等腰三角形有一个内角为110°,则这个等腰三角形的底角是( )
A.70°B.45°C.35°D.50°
6.空气的成分(除去水汽、杂质等)是:氮气约占78%,氧气约占21%,其他微量气体约占1%.要反映上述信息,宜采用的统计图是( )
A.条形统计图B.折线统计图
C.扇形统计图D.频数分布直方图
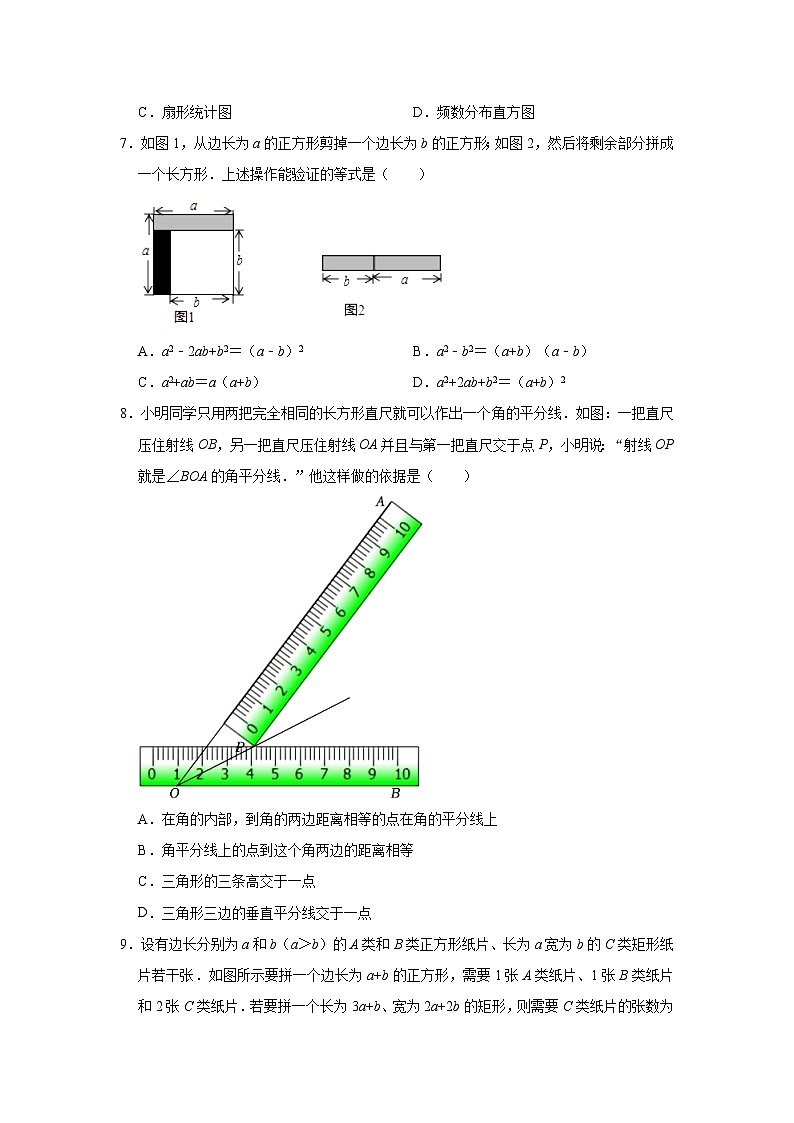
7.如图1,从边长为a的正方形剪掉一个边长为b的正方形;如图2,然后将剩余部分拼成一个长方形.上述操作能验证的等式是( )
A.a2﹣2ab+b2=(a﹣b)2B.a2﹣b2=(a+b)(a﹣b)
C.a2+ab=a(a+b)D.a2+2ab+b2=(a+b)2
8.小明同学只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
A.在角的内部,到角的两边距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形的三条高交于一点
D.三角形三边的垂直平分线交于一点
9.设有边长分别为a和b(a>b)的A类和B类正方形纸片、长为a宽为b的C类矩形纸片若干张.如图所示要拼一个边长为a+b的正方形,需要1张A类纸片、1张B类纸片和2张C类纸片.若要拼一个长为3a+b、宽为2a+2b的矩形,则需要C类纸片的张数为( )
A.6B.7C.8D.9
10.如图,在甲、乙、丙三只袋中分别装有球29个、29个、5个,先从甲袋中取出2x个球放入乙袋,再从乙袋中取出(2x+2y)个球放入丙袋,最后从丙袋中取出2y个球放入甲袋,此时三只袋中球的个数都相同,则2x+y的值等于( )
A.128B.64C.32D.16
二、填空题(每小题3分,共15分)
11.请写出一个比小的整数 .
12.若x+y=3,xy=2,则x2y+xy2的值为 .
13.血压包括收缩压和舒张压,分别代表心脏收缩时和舒张时的压力.收缩压的正常范围是:90~140mmHg,舒张压的正常范围是:60~90mmHg.现五人A、B、C、D、E的血压测量值统计如下:
则这五人中收缩压和舒张压均在正常范围内的人有 个.
14.将含30°角的直角三角板和直尺按如图所示的方式放置,已知∠α=60°,点B,C表示的刻度分别为1cm,3cm,则线段AB的长为 cm.
15.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADB的度数是 .
三、解答题(本大题共8个小题,满分75分)
16.(1)已知x+y﹣4=0,求2x•2y的值;
(2)先化简,再求值:(a﹣b)2﹣2a(a+3b)+(a+2b)(a﹣2b)其中a=1,b=﹣3.
17.学生的学业负担过重会严重影响学生对待学习的态度.为此某市教育部门对某学校的七年级学生对待学习的态度进行了一次调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中最小的扇形的圆心角的度数.
18.如图.已知锐角△ABC,∠B=48°,请用尺规作图法,在△ABC内部求作一点P.使PB=PC.且∠PBC=24°.(保留作图痕迹,不写作法)
19.如图,港口B在港口A的北偏东38°方向,且A、B之间的距离为75km.港口C在港口B的北偏西38°方向,且港口A的正北方向.求港口B与C之间的距离BC.
20.如图,点D,E分别在AB,AC上,∠ADC=∠AEB=90°,BE,CD相交于点O,OB=OC.
求证:∠1=∠2.
小虎同学的证明过程如下:
(1)小虎同学的证明过程中,第 步出现错误;
(2)请写出正确的证明过程.
21.如图,某社区有两块相连的长方形空地,一块长为(3a+2b)m,宽为(2a+b)m;另一块长为(a+b)m,宽为(a﹣b)m.现将两块空地进行改造,计划在中间边长为(a﹣b)m的正方形(阴影部分)中种花,其余部分种植草坪.
(1)求计划种植草坪的面积;
(2)已知a=30,b=10,若种植草坪的价格为30元/m2,求种植草坪应投入的资金是多少元?
22.阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0,(n﹣4)2=0,
∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)a2+b2﹣2a+1=0,则a= .b= .
(2)已知x2+2y2+2xy﹣6y+9=0,求xy的值.
(3)已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2﹣4a﹣6b+11=0,求△ABC的周长.
23.综合与实践:
问题探究:(1)如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9“平分一个已知角,”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在OA和OB上分别取点C和D,使得OC=OD,连接CD,以CD为边作等边三角形CDE,则OE就是∠AOB的平分线.请写出OE平分∠AOB的依据: ;
类比迁移:(2)小明根据以上信息研究发现:△CDE不一定必须是等边三角形,只需CE=DE即可,他查阅资料;我国古代已经用角尺平分任意角,做法如下:如图3,在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线OC是∠AOB的平分线,请说明此做法的理由;
拓展实践:(3)小明将研究应用于实践.如图4,校园的两条小路AB和AC,汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等,试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
参考答案
一、选择题(每小题3分,共30分)下列各小题均有四个答案,其中只有一个是正确的.
1.下列各数为无理数的是( )
A.0.618B.C.D.
【分析】明确无理数是无限不循环小数;有理数分为整数和分数.
解:∵=﹣3,
∴0.618;;均为有理数,是无理数.
故选:C.
【点评】本题考查实数的分类,明确无理数是无限不循环小数;有理数分为整数和分数.题目难度较小,多为考卷中第一题.
2.下列计算正确的是( )
A.(﹣3x)2=﹣9x2
B.7x+5x=12x2
C.(x﹣3)2=x2﹣6x+9
D.(x﹣2y)(x+2y)=x2+4y2
【分析】利用幂的乘方与积的乘方的性质,合并同类项的法则,完全平方公式和平方差公式对每个选项进行逐一判断即可得出结论.
解:∵(﹣3x)2=9x2,
∴A选项的运算不正确,不符合题意;
∵7x+5x=12x,
∴B选项的运算不正确,不符合题意;
∵(x﹣3)2=x2﹣6x+9,
∴C选项的运算正确,符合题意;
∵(x﹣2y)(x+2y)=x2﹣4y2,
∴D选项的运算不正确,不符合题意.
故选:C.
【点评】本题主要考查了整式的混合运算,幂的乘方与积的乘方的性质,合并同类项的法则,完全平方公式和平方差公式,熟练掌握上述性质与公式是解题的关键.
3.下列各式从左到右的变形,因式分解正确的是( )
A.(a+3)2=a2+6a+9
B.a2﹣4a+4=a(a﹣4)+4
C.5ax2﹣5ay2=5a(x+y)(x﹣y)
D.a2﹣2a﹣8=(a﹣2)(a+4)
【分析】本题考查因式分解﹣十字相乘,提公因式等相关知识.
解:A:(a+3)2=a2+6a+9是完全平方公式,不是因式分解的形式,故选项A错误,
B:a2﹣4a+4=(a﹣2)2,故选项B错误,
C:5ax2﹣5ay2=5a(x2﹣y2)=5a(x+y)(x﹣y),故选项C正确,
D:a2﹣2a﹣8=(a+2)(a﹣4),故选项D错误.
故答案为:C.
【点评】本题考查因式分解,提公因式等相关知识.解题的关键是能够熟悉因式分解的定义,熟练运用因式分解中的提公因式,十字相乘等方法.
4.如图,工人师傅设计了一种测零件内径AB的卡钳,卡钳交叉点O为AA′、BB'的中点.只要量出A′B′的长度.就可以知道该零件内径AB的长度.依据的数学基本事实是( )
A.两角和它们的夹边分别相等的两个三角形全等
B.两边和它们的夹角分别相等的两个三角形全等
C.三边分别相等的两个三角形全等
D.两点之间线段最短
【分析】根据点O为AA'、BB'的中点得出OA=OA',OB=OB',根据对顶角相等得到∠AOB=∠A'OB',从而证得△AOB和△A'OB'全等,于是有AB=A'B',问题得证.
解:∵点O为AA'、BB'的中点,
∴OA=OA',OB=OB',
由对顶角相等得∠AOB=∠A'OB',
在△AOB和△A'OB'中,
,
∴△AOB≌△A'OB'(SAS),
∴AB=A'B',
即只要量出A'B'的长度,就可以知道该零件内径AB的长度,
故选:B.
【点评】本题考查了三角形全等的判定与性质,正确运用三角形全等的判定定理是解题的关键.
5.若等腰三角形有一个内角为110°,则这个等腰三角形的底角是( )
A.70°B.45°C.35°D.50°
【分析】根据等腰三角形的性质进行计算,即可解答.
解:当等腰三角形的顶角为110°时,则它的底角==35°,
故选:C.
【点评】本题考查了等腰三角形的性质,三角形内角和定理,熟练掌握等腰三角形的性质,以及三角形内角和定理是解题的关键.
6.空气的成分(除去水汽、杂质等)是:氮气约占78%,氧气约占21%,其他微量气体约占1%.要反映上述信息,宜采用的统计图是( )
A.条形统计图B.折线统计图
C.扇形统计图D.频数分布直方图
【分析】根据扇形统计图的特点:①用扇形的面积表示部分在总体中所占的百分比.②易于显示每组数据相对于总数的大小即可得到答案.
解:氮气约占78%,氧气约占21%,其他微量气体约占1%.要反映上述信息,宜采用的统计图是扇形统计图.
故选:C.
【点评】此题考查的是扇形统计图的特点,掌握其特点是解决此题关键.
7.如图1,从边长为a的正方形剪掉一个边长为b的正方形;如图2,然后将剩余部分拼成一个长方形.上述操作能验证的等式是( )
A.a2﹣2ab+b2=(a﹣b)2B.a2﹣b2=(a+b)(a﹣b)
C.a2+ab=a(a+b)D.a2+2ab+b2=(a+b)2
【分析】由图1可知剩余部分的面积,由图2可求长方形的面积,两部分面积相等即可求解.
解:由图1可知剩余部分的面积=a2﹣b2,
由图2可求长方形的面积=(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),
故选:B.
【点评】本题考查平方差公式的几何背景;利用面积的关系验证平方差公式是解题的关键.
8.小明同学只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )
A.在角的内部,到角的两边距离相等的点在角的平分线上
B.角平分线上的点到这个角两边的距离相等
C.三角形的三条高交于一点
D.三角形三边的垂直平分线交于一点
【分析】由题意可知,点P到射线OB,OA的距离相等,则点P在∠BOA的平分线上,即可得出答案.
解:由题意可知,点P到射线OB的距离是直尺的宽度,点P到射线OA的距离也是直尺的宽度,
∴点P到射线OB,OA的距离相等,
∴点P在∠BOA的平分线上(在角的内部,到角的两边距离相等的点在角的平分线上).
故选:A.
【点评】本题考查角平分线的性质,理解题意,掌握角的内部到角的两边距离相等的点在角的平分线上是解答本题的关键.
9.设有边长分别为a和b(a>b)的A类和B类正方形纸片、长为a宽为b的C类矩形纸片若干张.如图所示要拼一个边长为a+b的正方形,需要1张A类纸片、1张B类纸片和2张C类纸片.若要拼一个长为3a+b、宽为2a+2b的矩形,则需要C类纸片的张数为( )
A.6B.7C.8D.9
【分析】用长乘宽,列出算式,根据多项式乘多项式的运算法则展开,然后根据A、B、C类卡片的形状可得答案.
解:∵(3a+b)(2a+2b)
=6a2+6ab+2ab+2b2
=6a2+8ab+2b2,
∴若要拼一个长为3a+b、宽为2a+2b的矩形,则需要C类纸片的张数为8张.
故选:C.
【点评】本题考查了多项式乘多项式在几何图形问题中的应用,数形结合并明确多项式乘多项式的运算法则是解题的关键.
10.如图,在甲、乙、丙三只袋中分别装有球29个、29个、5个,先从甲袋中取出2x个球放入乙袋,再从乙袋中取出(2x+2y)个球放入丙袋,最后从丙袋中取出2y个球放入甲袋,此时三只袋中球的个数都相同,则2x+y的值等于( )
A.128B.64C.32D.16
【分析】根据题意列出方程,分别求出2x和2y,再根据同底数幂乘法的逆运算求出2x+y即可.
解:由题意,得5﹣2y+2x+2y=29+2y﹣2x=29+2x﹣2x﹣2y,
即5+2x=29+2y﹣2x=29﹣2y,
∴
解得
∴2x+y=2x×2y=16×8=128,
故选:A.
【点评】本题考查指数幂的运算法则和方程思想,根据题意列出方程,并能对方程进行变形是解题的关键.
二、填空题(每小题3分,共15分)
11.请写出一个比小的整数 4(答案不唯一) .
【分析】根据算术平方根的定义估算无理数的大小即可.
解:∵42=16,52=25,而16<23<25,
∴4<<5,
∴比小的整数有4(答案不唯一),
故答案为:4(答案不唯一).
【点评】本题考查估算无理数的大小,理解算术平方根的定义是正确解答的前提.
12.若x+y=3,xy=2,则x2y+xy2的值为 6 .
【分析】把x+y和xy看作整体,利用提公因式对x2y+xy2进行分解,代入可得.
解:∵x+y=3,xy=2,
∴x2y+xy2=xy(x+y)=2×3=6.
故答案为:6.
【点评】本题考查了因式分解,关键把x+y和xy看作整体,然后利用提公因式对x2y+xy2进行分解,代入即可.
13.血压包括收缩压和舒张压,分别代表心脏收缩时和舒张时的压力.收缩压的正常范围是:90~140mmHg,舒张压的正常范围是:60~90mmHg.现五人A、B、C、D、E的血压测量值统计如下:
则这五人中收缩压和舒张压均在正常范围内的人有 3 个.
【分析】分析折线统计图即可得出结果.
解:观察图象可知:收缩压在正常范围的有A、B、D、E,
舒张压在正常范围的有B、C、D、E,
这五人中收缩压和舒张压均在正常范围内的人有B、D、E,
即3个.
故答案为:3.
【点评】本题考查了折线统计图,熟练识别折线统计图,从中获得准确信息是本题的关键.
14.将含30°角的直角三角板和直尺按如图所示的方式放置,已知∠α=60°,点B,C表示的刻度分别为1cm,3cm,则线段AB的长为 2 cm.
【分析】先由平行线的性质可得∠ACB的度数,根据等边三角形的判定和性质定理可得AB=BC,则可得出AB的长.
解:∵直尺的两对边相互平行,
∴∠ACB=∠α=60°,
∵∠A=60°,
∴∠ABC=180°﹣∠ACB﹣∠A=180°﹣60°﹣60°=60°,
∴∠A=∠ABC=∠ACB,
∴△ABC是等边三角形,
∴AB=BC=3﹣1=2(cm).
故答案为:2.
【点评】此题主要是考查了等边三角形的判定和性质,平行线的性质,能够得出AB=BC是解答此题的关键.
15.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,连接AD,若△ABD为直角三角形,则∠ADB的度数是 90°或50° .
【分析】首先根据等腰三角形的性质求出∠B=∠C=40°,然后分两种情况进行讨论:①∠ADB=90°;②∠BAD=90°,进而根据三角形的内角和定理求出∠ADB的度数即可.
解:∵在△ABC中,AB=AC,∠BAC=100°,
∴∠B=∠C=(180°﹣∠A)=40°,
∵△ABD为直角三角形,
∴有以下两种情况:
①∠ADB=90°,
②∠BAD=90°,
此时∠ADB=180°﹣∠BAD﹣∠B=180°﹣90°﹣40°=50°.
∴若△ABD为直角三角形,则∠ADB的度数是90°或50°.
故答案为:90°或50°.
【点评】此题主要考查了等腰三角形的性质,三角形的内角的定理,熟练掌握等腰三角形的性质,三角形的内角的定理是解答此题的关键;分类讨论是解答此题的难点,也是易错点之一.
三、解答题(本大题共8个小题,满分75分)
16.(1)已知x+y﹣4=0,求2x•2y的值;
(2)先化简,再求值:(a﹣b)2﹣2a(a+3b)+(a+2b)(a﹣2b)其中a=1,b=﹣3.
【分析】(1)先根据已知条件求出a+b,然后利用同底数幂的乘法法则进行计算即可;
(2)利用去括号法则和合并同类项法则进行化简,然后把a,b的值代入化简后的式子进行计算即可.
解:(1)∵x+y﹣4=0
∴x+y=4,
∴2x⋅2y
=2x+y
=24
=16;
(2)原式=a2﹣2ab+b2﹣2a2﹣6ab+a2﹣4b2
=a2+a2﹣2a2+b2﹣4b2﹣2ab﹣6ab
=﹣3b2﹣8ab,
当 a=1,b=﹣3 时,
原式=﹣3×(﹣3)2﹣8×1×(﹣3)
=﹣3×9+8×1×3
=﹣27+24
=﹣3.
【点评】本题主要考查了整式的化简求值,解题关键是熟练掌握同底数幂相乘法则、去括号法则和合并同类项法则
17.学生的学业负担过重会严重影响学生对待学习的态度.为此某市教育部门对某学校的七年级学生对待学习的态度进行了一次调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次调查中,共调查了 200 名学生;
(2)将图①补充完整;
(3)求出图②中最小的扇形的圆心角的度数.
【分析】(1)由A级人数及其所占百分比可得被调查的总人数;
(2)用总人数减去A、B级人数求出C级人数,据此可补全图形;
(3)用360°乘以C级人数所占比例即可.
解:(1)50÷25%=200(名),
答:此次抽样调查中,共调查了200名学生;
故答案为:200;
(2)C级学生人数为200﹣(50+120)=30(名),
补全图形如下:
(3)图②中C级所占的圆心角的度数为360°×=54°.
答:图②中最小的扇形的圆心角的度数为54°.
【点评】本题主要考查的是条形统计图与扇形统计图的综合运用.读懂统计图,从统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据,扇形统计图可以显示出每一部分在总体中所占的百分比.
18.如图.已知锐角△ABC,∠B=48°,请用尺规作图法,在△ABC内部求作一点P.使PB=PC.且∠PBC=24°.(保留作图痕迹,不写作法)
【分析】先作∠ABC的平分线BD,再作BC的垂直平分线l,直线l交BD于P点,则P点满足条件.
解:如图,点P即为所求.
【点评】本题考查了作图﹣复杂作图:解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了等腰三角形的性质.
19.如图,港口B在港口A的北偏东38°方向,且A、B之间的距离为75km.港口C在港口B的北偏西38°方向,且港口A的正北方向.求港口B与C之间的距离BC.
【分析】首先根据题意可得CN∥BD,可得∠BCA=∠DBC=38°,即可得∠BCA=∠A,再根据等腰三角形的判定,即可求解.
解:∵CN∥BD,
∴∠BCA=∠DBC=38°,
∴∠BCA=∠A=38°,
∴BC=AB=75km,
故港口B与C之间的距离BC为75km.
【点评】此题考查了方位角的应用,平行线的性质,等腰三角形的判定,解答本题的关键是将实际问题转化为数学模型进行求解.
20.如图,点D,E分别在AB,AC上,∠ADC=∠AEB=90°,BE,CD相交于点O,OB=OC.
求证:∠1=∠2.
小虎同学的证明过程如下:
(1)小虎同学的证明过程中,第 二 步出现错误;
(2)请写出正确的证明过程.
【分析】(1)根据全等三角形的判定定理判断;
(2)证明△DOB≌△EOC,根据全等三角形的性质得到OD=OE,再证明Rt△ADO≌Rt△AEO,得到∠1=∠2.
【解答】(1)解:小虎同学的证明过程中,第二步出现错误,
故答案为:二;
(2)证明:∵∠ADC=∠AEB=90°,
∴∠BDC=∠CEB=90°,
在△DOB和△EOC中,
,
∴△DOB≌△EOC(AAS),
∴OD=OE,
在Rt△ADO和Rt△AEO中,
,
∴Rt△ADO≌Rt△AEO(HL),
∴∠1=∠2,
方法二:∵OD=OE,∠ADC=∠AEB=90°,
∴∠1=∠2.
【点评】本题考查的是全等三角形的判定和性质,掌握三角形全等的判定定理是解题的关键.
21.如图,某社区有两块相连的长方形空地,一块长为(3a+2b)m,宽为(2a+b)m;另一块长为(a+b)m,宽为(a﹣b)m.现将两块空地进行改造,计划在中间边长为(a﹣b)m的正方形(阴影部分)中种花,其余部分种植草坪.
(1)求计划种植草坪的面积;
(2)已知a=30,b=10,若种植草坪的价格为30元/m2,求种植草坪应投入的资金是多少元?
【分析】(1)计划种植草坪的面积等于2个矩形的面积减去阴影部分的面积,利用多项式乘多项式法则,平方差公式和完全平方公式化简,去括号合并得到最简结果即可;
(2)将a与b的值代入(1)中求得的栽花面积和草坪面积,再根据总价=单价×数量计算即可求解.
解:(1)两块空地总面积:(3a+2b)×(2a+b)+(a+b)×(a﹣b),
=6a2+7ab+2b2+a2﹣b2
=7a2+7ab+b2,
栽花面积:(a﹣b)2=a2﹣2ab+b2,
草坪面积:7a2+7ab+b2﹣(a2﹣2ab+b2)=6a2+9ab.
(2)a=30,b=10,草坪价格为30元/m2,
应投入的资金=(6a2+9ab)×30=(6×302+9×30×10)×30=243000元.
【点评】本题考查了列代数式,多项式乘多项式,以及整式的混合运算﹣化简求值,弄清楚题意是解答本题的关键.
22.阅读材料:若m2﹣2mn+2n2﹣8n+16=0,求m、n的值.
解:∵m2﹣2mn+2n2﹣8n+16=0,
∴(m2﹣2mn+n2)+(n2﹣8n+16)=0,
∴(m﹣n)2+(n﹣4)2=0,
∴(m﹣n)2=0,(n﹣4)2=0,
∴n=4,m=4.
根据你的观察,探究下面的问题:
(1)a2+b2﹣2a+1=0,则a= 1 .b= 0 .
(2)已知x2+2y2+2xy﹣6y+9=0,求xy的值.
(3)已知△ABC的三边长a、b、c都是正整数,且满足2a2+b2﹣4a﹣6b+11=0,求△ABC的周长.
【分析】(1)先根据例题凑成2个完全平方式的和等于0的形式,再根据非负数的性质求得a、b的值即可解答;
(2)先根据例题凑成2个完全平方式的和等于0的形式,再根据非负数的性质求得x、y的值,最后代入xy即可解答;
(3)先先根据例题凑成3个完全平方式的和等于0的形式,再根据非负数的性质求得a、b、c的值,最后代入xy即可解答.
解:(1)∵a2+b2﹣2a+1=0,
∴a2﹣2a+1+b2=0,
∴(a﹣1)2+b2=0,
∴a﹣1=0,b=0,
∴a=1,b=0,
故答案为:1,0.
(2)∵x2+2y2+2xy﹣6y+9=0,
∴x2+y2+2xy+y2﹣6y+9=0,即:(x+y)2+(y﹣3)2=0,
∴x+y=0,y﹣3=0,
∴x=﹣3,y=3,
∴xy=(﹣3)3=﹣27.
(3)∵2a2+b2﹣4a﹣6b+11=0,
∴2a2﹣4a+2+b2﹣6b+9=0,
∴2(a﹣1)2+(b﹣3)2=0,
∴a﹣1=0,b﹣3=0,解得:a=1,b=3,
由三角形三边关系可知,三角形三边分别为1、3、3,
∴△ABC的周长为1+3+3=7.
【点评】本题考查了完全平方公式、非负数的性质,完全平方公式、在记忆相关知识点是解题的关键.
23.综合与实践:
问题探究:(1)如图1是古希腊数学家欧几里得所著的《几何原本》第1卷命题9“平分一个已知角,”即:作一个已知角的平分线,如图2是欧几里得在《几何原本》中给出的角平分线作图法:在OA和OB上分别取点C和D,使得OC=OD,连接CD,以CD为边作等边三角形CDE,则OE就是∠AOB的平分线.请写出OE平分∠AOB的依据: SSS ;
类比迁移:(2)小明根据以上信息研究发现:△CDE不一定必须是等边三角形,只需CE=DE即可,他查阅资料;我国古代已经用角尺平分任意角,做法如下:如图3,在∠AOB的边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同刻度分别与点M,N重合,则过角尺顶点C的射线OC是∠AOB的平分线,请说明此做法的理由;
拓展实践:(3)小明将研究应用于实践.如图4,校园的两条小路AB和AC,汇聚形成了一个岔路口A,现在学校要在两条小路之间安装一盏路灯E,使得路灯照亮两条小路(两条小路一样亮),并且路灯E到岔路口A的距离和休息椅D到岔路口A的距离相等,试问路灯应该安装在哪个位置?请用不带刻度的直尺和圆规在对应的示意图5中作出路灯E的位置.(保留作图痕迹,不写作法)
【分析】(1)由等边三角形的性质得CE=DE,再证△OCE≌△ODE(SSS),得∠COE=∠DOE,即可得出结论;
(2)证△OCM≌△OCN(SSS),得∠AOC=∠BOC,即可得出结论;
(3)先作∠BAC的平分线AK,再在AK上截取AE=AD即可.
解:(1)∵△CDE是等边三角形,
∴CE=DE,
又∵OC=OD,OE=OE,
∴△OCE≌△ODE(SSS),
∴∠COE=∠DOE,
∴OE是∠AOB的平分线,
故答案为:SSS;
(2)∵OM=ON,CM=CN,OC=OC,
∴△OCM≌△OCN(SSS),
∴∠AOC=∠BOC,
∴射线OC是∠AOB的平分线;
(3)如图,
点E即为所求的点.
【点评】本题是三角形综合题目,考查了全等三角形的判定与性质、等边三角形的性质、角平分线定义以及尺规作图等知识,熟练掌握角平分线定义和等边三角形的性质,证明三角形全等是解题的关键,属于中考常考题型.
证明:∵∠ADC=∠AEB=90°,
∴∠DOB+∠B=∠EOC+∠C=90°.
∵∠DOB=∠EOC,
∴∠B=∠C.……第一步
又OA=OA,OB=OC,
∴△ABO≌△ACO.……第二步
∴∠1=∠2.……第三步
证明:∵∠ADC=∠AEB=90°,
∴∠DOB+∠B=∠EOC+∠C=90°.
∵∠DOB=∠EOC,
∴∠B=∠C.……第一步
又OA=OA,OB=OC,
∴△ABO≌△ACO.……第二步
∴∠1=∠2.……第三步
相关试卷
这是一份2023-2024学年河南省南阳市油田九年级(上)期末数学试卷(含解析),共20页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年河南省南阳市油田七年级(上)期末数学试卷(含解析),共18页。试卷主要包含了选择题,填空题,计算题,解答题等内容,欢迎下载使用。
这是一份2022-2023学年河南省南阳市油田七年级(下)期末数学试卷(含解析),共19页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。








