湘教版八年级下册2.1 多边形教案

这是一份湘教版八年级下册2.1 多边形教案，共6页。

课题
2.1多边形（2）
单元
1
学科
数学
年级
八
学习
目标
情感态度和价值观目标
通过对生活中数学问题的探究，进一步提高学数学、用数学的意识，在自主探究、合作交流的过程中，体会数学的重要作用，感受数学活动的重要意义和合作成功的喜悦，提高学生学习的热情。
能力目标
经历质疑、猜想、归纳等活动，发展学生的合情推理能力，积累数学活动的经验，在探索中学会与人合作，学会交流自己的思想和方法
知识目标
掌握多边形外角和定理，进一步了解转化的数学思想
重点
多边形的外角和等于360度
难点
如何引导学生通过自主学习, 探索多边形外角和为什么都正好是360度。
学法
自主探究，合作交流
教法
多媒体，问题引领
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
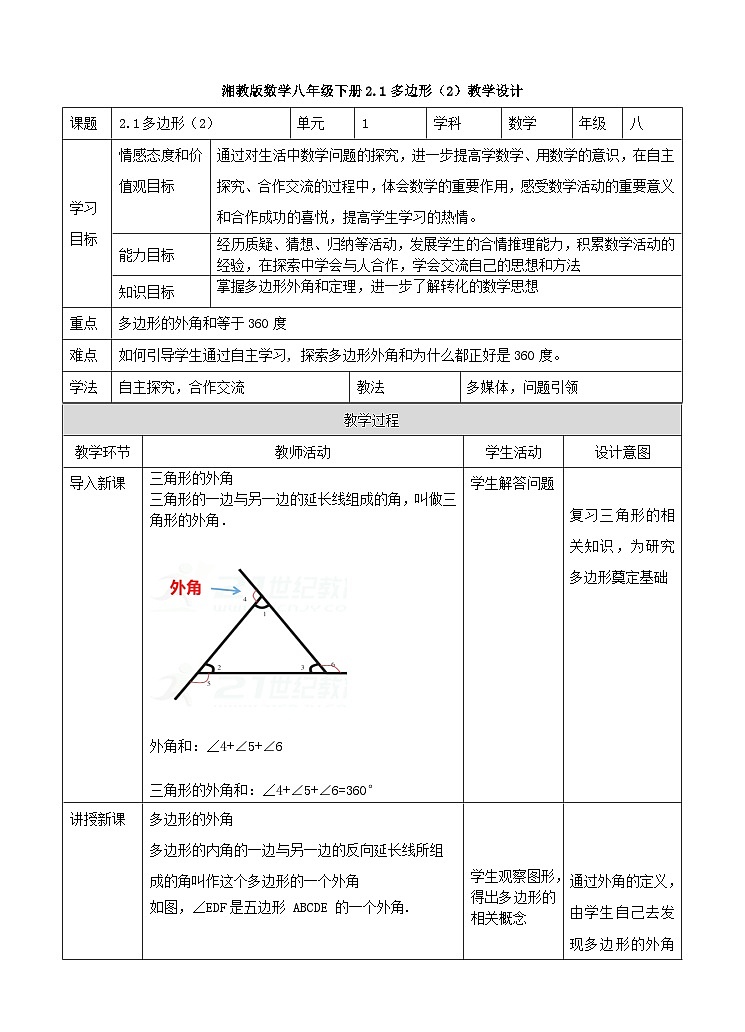
三角形的外角
三角形的一边与另一边的延长线组成的角，叫做三角形的外角．
外角和：∠4+∠5+∠6
三角形的外角和：∠4+∠5+∠6=360°
学生解答问题

复习三角形的相关知识，为研究多边形奠定基础
讲授新课
多边形的外角
多边形的内角的一边与另一边的反向延长线所组成的角叫作这个多边形的一个外角
如图，∠EDF是五边形 ABCDE 的一个外角.
多边形的外角和
在多边形的每个顶点处取一个外角，它们的和叫作这个多边形的外角和．
注意：
一般地，在多边形的任一顶点处按顺(逆)时针方向可作外角，n边形有n个外角
动脑筋
我们已经知道三角形的外角和为360°，那么四边形的外角和为多少度呢？
如图， 在四边形ＡBCＤ的每一个顶点处取一个外角， 如∠1， ∠2，∠3，∠4.
∵ ∠1+∠DAB=180°，∠2+∠ABC=180°， ∠3+∠BCD=180°，∠4+∠ADC=180°，
又 ∠DAB+∠ABC+∠BCD+∠ADC=360°，
∴ ∠1+∠2+∠3+∠4=4×180°-360°=360°.
∴ 四边形的外角和为360°
分别求出下列多边形的外角和的度数
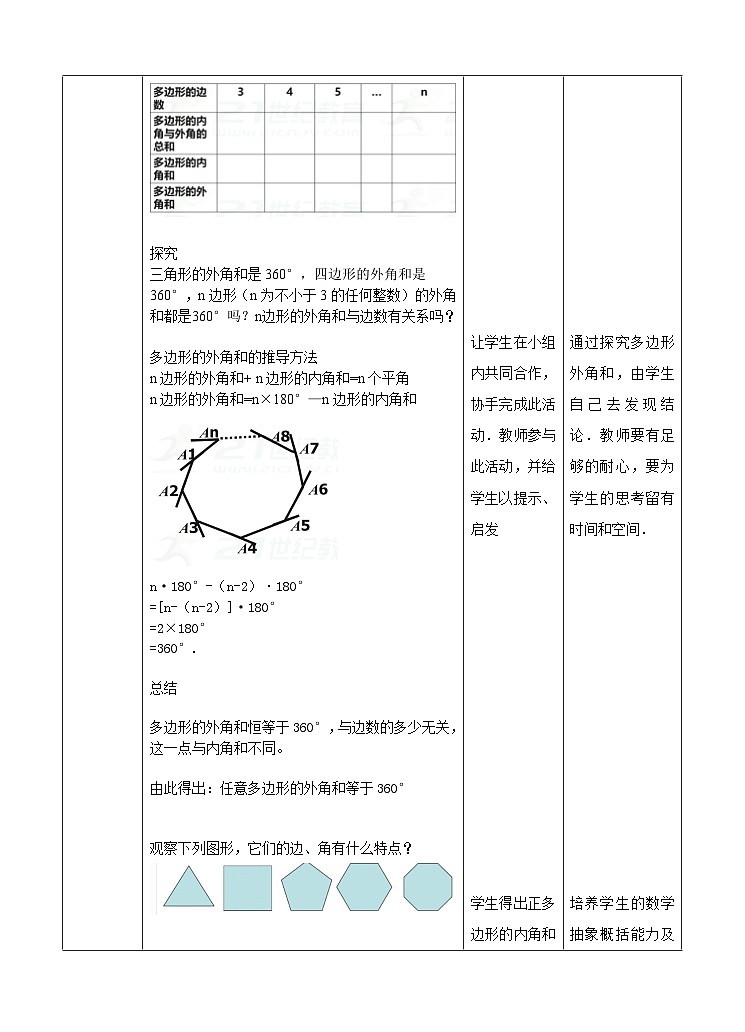
探究
三角形的外角和是360°，四边形的外角和是
360°，n边形（n为不小于3的任何整数）的外角和都是360°吗？n边形的外角和与边数有关系吗？
多边形的外角和的推导方法
n边形的外角和+ n边形的内角和=n个平角
n边形的外角和=n×180°—n边形的内角和
n·180°-（n-2）·180°
=[n-（n-2）]·180°
=2×180°
=360°.
总结
多边形的外角和恒等于360°，与边数的多少无关，这一点与内角和不同。
由此得出：任意多边形的外角和等于360°
观察下列图形，它们的边、角有什么特点？
上面正多边形的一个内角和外角各是多少度？
正多边形每个内角度数的计算公式：
或180°－
正多边形每个外角度数的计算公式：
例1、一个多边形的内角和等于它外角和的５倍，它是几边形？
练习：
一个正多边形的每个内角比相邻外角大36°求这个多边形的边数。
观察:
三角形具有稳定型，那么四边形呢？用4根木条钉成如图的木框，任意扭转四边形的边，它的形状会发生变化吗？
我们发现，四边形的边长不变，但它的形状改变了，这说明四边形具有不稳定性.
在实际生活中，我们经常利用四边形的不稳定性，如上图a中电动伸缩门，图b中的升降机.有时又要克服四边形的不稳定性，例如图c中的栅栏两横梁之间加钉斜木条，构成三角形，这是为了利用三角形的稳定性.
学生观察图形，得出多边形的相关概念
让学生在小组内共同合作，协手完成此活动．教师参与此活动，并给学生以提示、启发
让学生在小组内共同合作，协手完成此活动．教师参与此活动，并给学生以提示、启发
学生得出正多边形的内角和以及外角和的公式。
学生自主解答例题，教师巡视学生的结果
学生观察图形，得出四边形的不稳定性，并举出现实中的例子
通过外角的定义，由学生自己去发现多边形的外角和的表示方法．教师要有足够的耐心，要为学生的思考留有时间和空间．
培养学生的数学抽象概括能力及理性精神.
让学生体验成功
通过探究多边形外角和，由学生自己去发现结论．教师要有足够的耐心，要为学生的思考留有时间和空间．
培养学生的数学抽象概括能力及理性精神.
让学生体验成功
通过此题的解答，充分调动学生动脑的积极性，培养学生发散思维。
进一步理解和掌握四边形的不稳定性，提高学生的数学应用意识和逻辑推理能力．
巩固提升
1、若一个多边形的内角和小于其外角和，则这个多边形的边数是( )
A.3 B.4 C.5 D.6
答案：A
2、四边形不具有稳定性，当四边形形状改变时，发生变化的是( )
A.四边形的边长 B.四边形的周长
C.四边形的某些角的大小 D.四边形的内角和
答案：C
3.正八边形的每个外角都等于__________度.
答案： 45°
4. 一个多边形的内角和比它的外角和的3倍少180°，则它的边数是__________.
答案：7
5.一个多边形的每一个外角都等于30°，则该多边形的内角和等于__________.
答案：1800°
6、某多边形的内角和与外角和的总和为2160°，求此多边形的边数.
答案：
解：设这个多边形的边数为n，根据题意得
(n-2)·180+360=2 160.
解得x=12.
所以此多边形的边数是12.
7.多边形的内角和与某一外角的度数总和为1 350°，那么这个多边形的边数是多少？
答案：
解：设边数为n，外角为x°，则x+(n-2)×180=1350.
∴x=1350-180(n-2).
∵0 ∴0<1350-(n-2)×180<180.解得 ∵n为整数，
∴n=9.
学生自主解答，教师讲解答案。
鼓励学生认真思考；发现解决问题的方法，引导学生主动地参与教学活动，发扬数学民主，让学生在独立思考、合作交流等数学活动中，培养学生合作互助意识，提高数学交流与数学表达能力。
课堂小结
谈一谈本节的主要内容，畅所欲言聊收获。
学生归纳本节所学知识
培养学生总结，归纳的能力。
板书