初中数学湘教版八年级下册2.5.1矩形的性质教学设计

这是一份初中数学湘教版八年级下册2.5.1矩形的性质教学设计，共10页。

课题
矩形的性质
单元
2
学科
数学
年级
八
学习
目标
情感态度和价值观目标
培养严谨的推理能力，以及自主合作的精神，体会逻辑推理的思维价值
能力目标
经历探索矩形的概念和性质的过程，发展学生合情推理的意识；掌握几何思维方法。并渗透运动联系、从量变到质变的观点
知识目标
1.掌握矩形的概念和性质，理解矩形与平行四边形的区别与联系．
2.会初步运用矩形的概念和性质来解决有关问题．
重点
矩形的性质
难点
矩形的性质的灵活应用
学法
自主探究，合作交流
教法
多媒体，问题引领
教学过程
教学环节
教师活动
学生活动
设计意图
导入新课
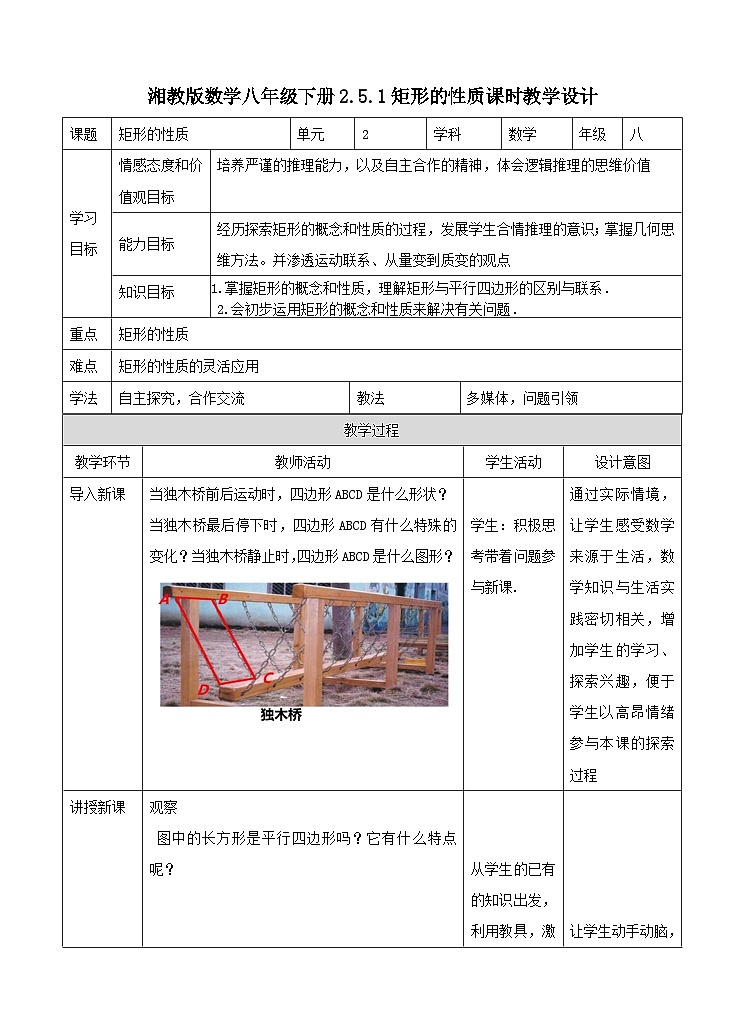
当独木桥前后运动时，四边形ABCD是什么形状？
当独木桥最后停下时，四边形ABCD有什么特殊的变化？当独木桥静止时，四边形ABCD是什么图形？
学生：积极思考带着问题参与新课.
通过实际情境，让学生感受数学来源于生活，数学知识与生活实践密切相关，增加学生的学习、探索兴趣，便于学生以高昂情绪参与本课的探索过程
讲授新课
观察
图中的长方形是平行四边形吗？它有什么特点呢？

如图，这是一个活动框架，改变这个平行四边形的形状，你会发现什么?
矩形的定义：
有一个角是直角的平行四边形叫做矩形，也称为长方形。
矩形是特殊的平行四边形。
想一想：
你能举出在人们的日常生活和生产实践中，有哪些东西是矩形的？

矩形的一般性质：
1.矩形的两组对边分别平行
2.矩形的两组对边分别相等
动脑筋
矩形是一个特殊的平行四边形，除了具有平行四边形的所有性质外，还有哪些特殊性质呢？
当平行四边形ABCD的一个∠ABC为直角时,观察其它角
猜想1：矩形的四个角都是直角．
已知：如图，四边形ABCD是矩形
求证：∠A=∠B=∠C=∠D=90°
证明： ∵四边形ABCD是矩形。
∴ ∠A=90°
又矩形ABCD是平行四边形
∴ ∠A=∠C ∠B = ∠D
∠A +∠B =180°
∴ ∠A=∠B=∠C=∠D=90°
即矩形的四个角都是直角
矩形的特殊性质
矩形的四个角都是直角
数学语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90°
当平行四边形ABCD的一个∠ABC为直角时,观察其对角线AC、BD的长度有何变化？
猜想2：矩形的对角线相等．
已知：如图,四边形ABCD是矩形
求证：AC =BD
证明：在矩形ABCD中
∵∠ABC = ∠DCB = 90°
又∵AB = DC ， BC = CB
∴△ABC≌△DCB
∴AC = BD 即矩形的对角线相等
矩形的特殊性质
矩形的对角线相等
数学语言
∵四边形ABCD是矩形
∴AC = BD
矩形特殊的性质
从角上看：矩形的四个角都是直角．
从对角线上看：矩形的两条对角线相等，且互相平分
例1 如图，矩形ABCD的两条对角线AC、BD相交于点O, AC= 4cm ，∠AOB=60°。求BC的长。
练习：
矩形ABCD中,AC、BD相交于点O，AB=6，BC=8，则△ABO的周长为_____。
做一做
画出一个矩形ABCD，把它减下来，怎样折叠能使矩形在折痕两旁的部分互相重合？满足这个要求的折叠方法有几种？由此猜测：矩形是轴对称图形吗？如果是，它有几条对称轴？你的猜测正确吗？
猜测：矩形是轴对称图形，有两条对称轴。
矩形是轴对称图形,过每一组对边中点的直线都是矩形的对称轴.
试着去证明猜测吧！
解： ∵四边形ABCD是矩形
∴OA=
∵E是AB的中点
∴EF垂直平分AB
∴点A、B关于直线EF对称，同理：点C、D关于直线EF对称
∴矩形关于直线EF对称，同理：矩形关于直线MN对称
已知四边形ABCD是矩形
相等的线段：AB=CD AD=BC AC=BD
OA=OC=OB=OD=
相等的角：∠DAB=∠ABC=∠BCD=∠CDA=90°
∠AOB=∠DOC ∠AOD=∠BOC
∠OAB=∠OBA=∠ODC=∠OCD
∠OAD=∠ODA=∠OBC=∠OCB
全等三角形有： Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB △OAB≌△OCD △OAD≌△OCB
等腰三角形有：△OAB,△OBC,△OCD,△OAD
直角三角形有：
Rt△ABC,Rt△BCD,Rt△CDA,Rt△DAB
总结
从学生的已有的知识出发，利用教具，激发学生的强烈的好奇心和求知欲。学生经历了将实际问题转化为数学问题的建模过程。
学生举出生活中的例子
并总结矩形的一般性质
自主归纳并组织语言作答，交流与讨
论，在教师
的引导下探
究矩形的性
质的证明方
法。启发学生分析，引导学生归纳探究，层层理清命题证明的思路，简化证明方法。
试着证明矩形的对角线相等。
试着总结矩形的特殊性质
教师引导学生审题，学生弄清题意后，师生共同分析思路，教师渗透综合分析法。
学生口答，教师板书解题过程。
学生动手操作，猜测矩形的对称轴并证明自己的猜测。
学生观察图形，总结矩形ABCD中的相关知识
让学生动手动脑，自主发现和认识矩形定义。 并运用了类比和比较的方式，让学生加深对定义的理解
让学生在特定的数学活动中经历矩形性质的形成过程，通过操作、
观察、分析、推
理、归纳总结出
了一般性的结
论。
师生共同完成推理过程。引导学生多角度多方位思考问题
培养学生独立思考，总结归纳的能力。
学生审题是解题的关键，通过运用矩形的性质学会解决简单的实际问题，培养了学生的应用意识。
培养学生动手，独立思考，总结归纳的能力。
培养学生独立思考，观察并总结归纳的能力。
巩固提升
1.如图，在矩形ABCD中，若AC=2AB，则∠AOB的大小是( )
A.30°B.45°C.60°D.90°
答案：C
2.如图，矩形ABCD的对角线AC，BD相交于点O，CE∥BD，DE∥AC.若AC=4，则四边形CODE的周长是( )
A.4 B.6 C.8 D.10
答案：C
3.如图，在矩形ABCD中，对角线AC，BD相交于点O，点E，F分别是AO，AD的中点，若AB=6 cm，BC=8 cm，则△AEF的周长=__________cm. .
答案：9
4. 如图，矩形ABCD中，点E,F分别是AB,CD的中点，连接DE和BF，分别取DE,BF的中点M,N，连接AM,CN,MN，若AB=2 ，BC=2 ，则图中阴影部分的面积为__________.

答案： 2
5、四个学生正在做投圈游戏，他们分别站在一个矩形的四个顶点处，目标物放在对角线的交点处，这样的队形对每个人公平吗？为什么？
答案：
答：公平
∵四边形ABCD是矩形，
∴AC＝2OA=2OC， BD=20B=2OD.
AC=BD，
∴OA=OB=OC=OD.
拓展延伸
如图，四边形ABCD是矩形，试利用矩形的性质说明：在直角三角形ABC斜边AC上的中线BD等于斜边的一半.
解：∵四边形ABCD为矩形
∴OA=OB=OC=OD=
直角三角形ABC斜边AC上的中线BO等于斜边的一半.
学生自主解答，教师讲解答案。
通过这几道题目来反馈学生对本节所学知识的掌握程度，落实基础。学生刚刚接触到新的知识需要一个过程，也就是对新知识从不熟悉到熟练的过程，无论是基础的习题，还是变式强化，都要以学生理解透彻为最终目标。
课堂小结
这节课你有哪些收获？你认为自己的表现如何？
1.矩形定义：
有一个角是直角的平行四边形叫矩形.
2.矩形的性质
矩形的对边平行且相等
矩形的四个角均为直角
矩形的对角线互相平分且相等
学生归纳本节所学知识
回顾、总结、提高。学生自觉形成本节的课的知识网络
板书
矩形的性质
矩形的定义：
有一个角是直角的平行四边形叫做矩形，也称为长方形。
矩形是特殊的平行四边形。