浙江省温州市2023-2024学年九年级上学期期末数学试题

这是一份浙江省温州市2023-2024学年九年级上学期期末数学试题，共20页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
本试卷分为选择题和非选择题两个部分，共4页，考试时间90分钟，全卷满分100分．答题时请在答题纸答题区域作答，不得超出答题区域边框线．
选择题部分
一、选择题（本题有10小题，每小题3分，共30分．每小题只有一个选项是正确的，不选、多选、错选均不给分）
1. 抛物线y＝﹣3（x﹣4）2+5的顶点坐标是（ ）
A. （4，5）B. （﹣4，5）C. （4，﹣5）D. （﹣4，﹣5）
【答案】A
【解析】
【分析】已知抛物线解析式为顶点式，可直接写出顶点坐标．
【详解】解：∵抛物线的解析式为y＝﹣3（x﹣4）2+5，
∴其顶点坐标为：（4，5）．
故选：A．
【点睛】本题考查了二次函数的性质，将解析式化为顶点式，顶点坐标是，对称轴是直线．
2. 已知点P到圆心O的距离为5，若点P在圆内，则的半径可能为（ ）
A. 3B. 4C. 5D. 6
【答案】D
【解析】
【分析】由点与圆的位置关系可知，的半径，进而可得出结果．
【详解】解：由点与圆的位置关系可知，的半径
故选D．
【点睛】本题考查了点与圆的位置关系．解题的关键在于对知识的熟练掌握．
3. 如图是海上风力发电装置，相同的三个转子叶片呈均匀分布．若图案绕中心旋转后能与原图案重合，则可以取（ ）您看到的资料都源自我们平台，家威杏 MXSJ663 低至0.3/份
A. 90B. 120C. 150D. 180
【答案】B
【解析】
【分析】本题考查旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．该图形被平分成三部分，因而每部分被分成的圆心角是．
【详解】解：∵该图形被平分成三部分，
∴，
故选：B．
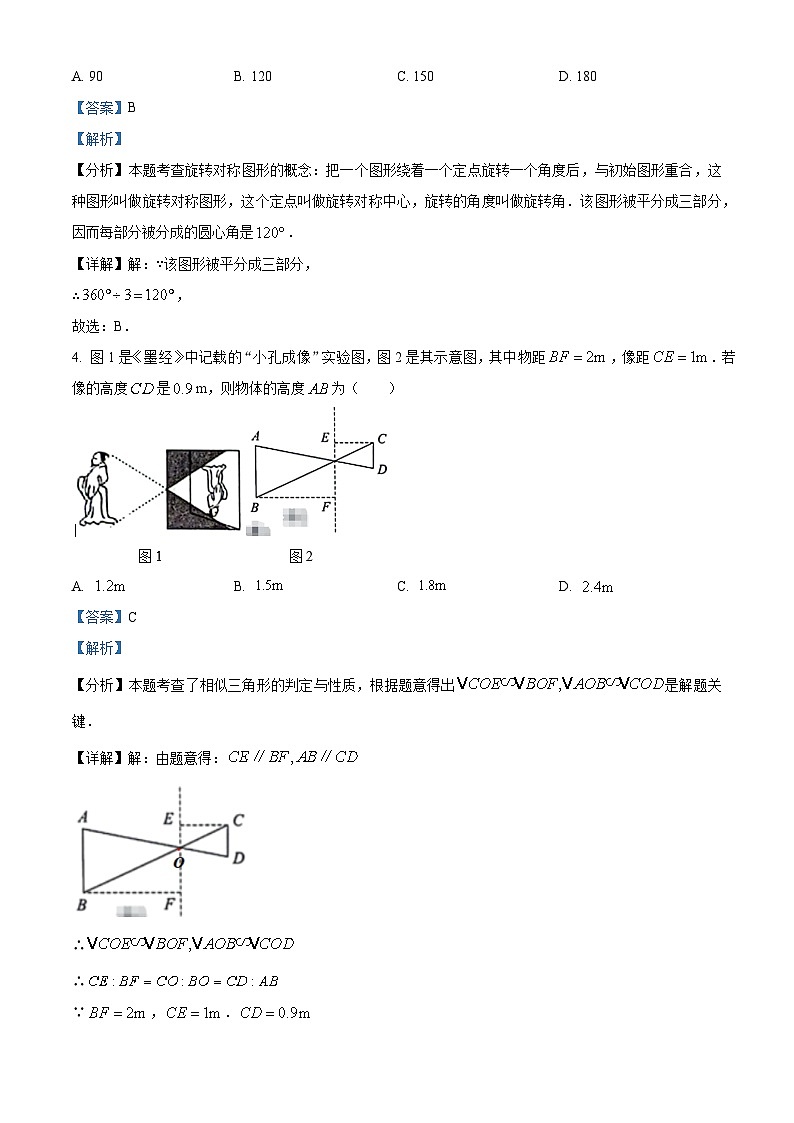
4. 图1是《墨经》中记载的“小孔成像”实验图，图2是其示意图，其中物距，像距．若像的高度是m，则物体的高度为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查了相似三角形的判定与性质，根据题意得出是解题关键．
【详解】解：由题意得：
∴
∴
∵，．
∴
∴物体的高度为
故选：C
5. 一个不透明的盒子内装有1个红球，1个黄球，1个蓝球，它们除颜色外其余均相同．现从中随机摸出一球，记下颜色后放回搅匀，如此继续．如表是小温前两次摸球的情况，当小温第三次摸球时，下列说法正确的是（ ）
A. 一定摸到红球B. 一定摸不到红球
C. 摸到黄球比摸到蓝球的可能性大D. 摸到红球、黄球和蓝球的可能性一样大
【答案】D
【解析】
【分析】本题考查概率公式，分别求出三种颜色球的概率再判断即可．
【详解】由题意得，摸到红球的概率为，摸到黄球的概率为，摸到蓝球的概率为，
∴摸到红球、黄球和蓝球的可能性一样大．
故选：D．
6. 一个不透明的盒子内装有1个红球，1个黄球，1个蓝球，它们除颜色外其余均相同．现从中随机摸出一球，记下颜色后放回搅匀，如此继续．小州摸球两次，则出现相同颜色的概率为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】本题考查列表法与树状图法，熟练掌握列表法与树状图法以及概率公式是解答本题的关键．画树状图得出所有等可能的结果数以及出现相同颜色的结果数，再利用概率公式可得出答案．
【详解】解：画树状图如下：
共有9种等可能的结果，其中出现相同颜色的结果有3种，
∴出现相同颜色的概率为．
故选：C．
7. 已知二次函数的图象如图所示，则点所在的象限是（ ）
A. 第一象限B. 第二象限C. 第三象限D. 第四象限
【答案】B
【解析】
【分析】此题考查了二次函数系数与图象的关系．注意二次函数系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线确定的．由开口向下，可得，由抛物线与y轴交于正半轴，可得，又由对称轴在y轴右侧，即可得a，b异号，继而求得答案．
【详解】解：∵开口向下，
∴，
∵抛物线与y轴交于正半轴，
∴，
∵对称轴在y轴右侧，
∴a，b异号，即，
∴，
∴点在第二象限．
故选：B．
8. 如图，内接于，为直径，半径，连结，．若，则的度数为（ ）
A. B. C. D.
【答案】C
【解析】
【分析】此题考查平行线的性质、圆周角定理等知识，由为的直径，，得，，由，，则，所以，于是得到问题的答案．
【详解】解：∵为的直径，，
∴，，
∵，
∴，
∴，
∴，
故选：C．
9. 如图，在中，，在上取点，使，延长至点，使得．若，则等于（ ）
A. B. C. D.
【答案】A
【解析】
【分析】本题主要考查了等腰三角形的性质和相似三角形的判定与性质．熟练掌握以上知识是解题的关键．先通过证明，再证明，最后得出即可．
【详解】解：，
，
，
，
，
，
，
，
，
，
，
，
，
．
故选：A．
10. 已知抛物线，当时，．若将抛物线向左平移4个单位后经过点，则的值为（ ）
A B. C. D.
【答案】D
【解析】
【分析】本题考查抛物线与x轴的交点，平移的性质以及二次函数的性质，关键是掌握平移的性质和二次函数的性质．先根据平移的性质得出抛物线过点，然后求出抛物线对称轴，再根据二次函数的性质得出当时，y有最小值，从而得出结论．
【详解】解：∵将抛物线向左平移4个单位后经过点，
∴抛物线过点，
∴，
解得，
∴抛物线对称轴为直线，
∴抛物线与x轴的另一交点为，
又∵当时，，
∴当时，y有最小值，
∴，
∴，
故选：D．
二、填空题（本题有6个小题，11-15每小题3分，16题4分，共19分）
11. 若一个正多边形的每一个外角都是，则该正多边形的边数是_______．
【答案】10
【解析】
【分析】本题考查多边形外角与边数的关系，正多边形的边数等于除以每一个外角的度数．
【详解】解：∵一个正多边形的每一个外角都是，
∴边数．
故答案为：10．
12. 某扇形的圆心角为，扇形的半径为4，则此扇形弧长为______．（结果保留）
【答案】
【解析】
【分析】根据弧长公式可进行求解．
【详解】解：由题意得：此扇形弧长为；
故答案为：．
【点睛】本题主要考查弧长公式，熟练掌握弧长的计算公式是解题的关键．
13. 某次踢球，足球飞行高度（米）与水平距离（米）之间满足，则足球从离地到落地的水平距离为_____米．
【答案】
【解析】
【分析】本题考查了二次函数的应用，依题意令，求出的值即可，解题的关键是熟练掌握二次函数的性质．
【详解】解：由题意得，当时，，
解得：，，
∴足球从离地到落地的水平距离为米，
故答案为：．
14. 如图，四边形内接于圆，点在上，若，，，则为______度．
【答案】25
【解析】
【分析】本题考查了圆内接四边形的性质以及圆周角定理，解题的关键是熟练掌握相关性质并灵活运用．连接、，先根据圆内接四边形的性质求出，然后根据，求出即可解答．
【详解】解：连接、，
，
，
，
，
．
故答案为：25．
15. 如图，在中，，点在上，作于点，将绕点逆时针旋转至，点，分别落在，上．若，，则______．
【答案】
【解析】
【分析】根据将绕点逆时针旋转至，，可得，，，即得，证明，可得，故，而，故：，可解得．
【详解】
将绕点逆时针旋转至．
，，
根据勾股定理可得：
在和中，
，
根据平行线分线段对应成比例可知：
即：
解得：
故答案为：．
【点睛】本题考查旋转的性质及应用，涉及全等三角形的判定与性质、平行线分线段对应成比例、勾股定理等，解题的关键是掌握全等三角形判定定理．
16. 【情境】图1是某庭院所砌的一堵带有月洞门的墙，其设计图（图2）是轴对称图形，对称轴交圆弧于点，墙面为正方形，门洞上方匾额的中点，，，分别是上方两个矩形对角线的交点．已知米，米，米，米．
【问题】月洞门所在圆半径为______米，匾额的长与宽之比为______．

图1 图2
【答案】 ①. ②.
【解析】
【分析】本题考查了垂径定理，相似三角形的判定与性质等知识点．设圆心为点，半径为，连接，①根据垂径定理即可求解；②证即可求解；
【详解】解：如图所示：设圆心为点，半径为，连接，
由题意可知：，
∴，
解得：
∵
∴
∴
∵，
∴
∴
∴匾额的长与宽之比为：
故答案为：①，②．
三、解答题（本题有6小题，共51分，解答需写出必要的文字说明、演算步骤或证明过程）
17. 已知线段，，满足．
（1）求的值．
（2）当线段是线段，的比例中项，且时，求的值．
【答案】（1）1 （2）
【解析】
【分析】本题考查比例线段，解题的关键是理解比例线段的定义，属于中考常考题型．
（1）由题意，，利用整体代入的思想解决问题；
（2）判断出a，b的值，再根据比例中项的定义求解．
【小问1详解】
解：，
，
；
【小问2详解】
解：，，
．
18. 某校七年级社会实践，安排三辆车，编号分别为，，．小温与小州都可以从这三辆车中任意选择一辆搭乘．
（1）求小温没有搭乘车的概率．
（2）若小温没有搭乘车，请用画树状图或列表的方法，求出小温与小州不同车的概率．
【答案】（1）
（2）
【解析】
【分析】本题主要考查用列表法或树状图法求事件发生的概率：
（1）直接利用概率公式求解即可；
（2）先列表得到所有的等可能结果，再找到符合条件的结果数，然后利用概率公式求解即可．
【小问1详解】
解：小温没有搭乘车的概率为；
【小问2详解】
解：列表如下：
由表可知，共有6种等可能结果，其中小温和小州搭不同车的结果有4种，
小温和小州搭不同车的概率为．
19. 如图，，，三点都在方格纸的格点上，请按要求在方格纸内作图．
（1）在图1中以点为位似中心，作线段的位似图形，使其长度为的2倍．
（2）已知的三边比为，在图2中画格点，使与相似．
【答案】19. 见解析 20. 见解析
【解析】
【分析】本题考查了位似图形的作图以及勾股定理的运算，掌握分类讨论的数学思想是解决第二问的关键．
（1）连接并等倍延长即可完成作图；
（2）由题意得是直角三角形，所以也是直角三角形；根据图示得，可得的三边长为：或或（舍）．
【小问1详解】
解：如图所示：
【小问2详解】
解：∵的三边比为，
且，
∴是直角三角形，
∴也是直角三角形，
由图可知：
∴的三边长为：或或（舍）
如图所示：
20. 如图，抛物线经过点，，与轴交于点．
（1）求抛物线的表达式及点坐标．
（2）点是抛物线上一点，且当时，的最大值为3，求的面积．
【答案】（1），点为
（2）
【解析】
【分析】本题主要考查了二次函数的图象和性质．求抛物线的表达式以及与面积有关的综合问题.
（1）用待定系数法求出抛物线的表达式，以及当当时，即可求出C点的坐标．
（2）根据时，的最大值为3，可确定m的值，进而可求出答案．
【小问1详解】
解：把，代入，
得，
解得：，
；
当时，，
∴点为．
【小问2详解】
由题意得，二次函数经过点
由（1）得，，，；
，
21. 如图，在中，，点在边上，的外接圆交于点，，过点作于点，延长交于点．

（1）求证：．
（2）求证：．
（3）若，，求的长．
【答案】（1）见解析 （2）见解析
（3）
【解析】
【分析】本题考查了圆周角定理，勾股定理，相似三角形的性质与判定．
（1）根据，得到，利用圆周角定理即可得出结果；
（2）由，得到，推出，证明，即可得出结论；
（3）设，，求出，由，得到，证明，根据相似三角形的性质即可得出结果．
小问1详解】
证明：，
，
，，
，
；
【小问2详解】
证明：，
，
，
，
；
【小问3详解】
解：，
设，，
在中，，
，，
，，
，
，，
，
，，
，
．
22. 综合与实践：设计公交车停靠站的扩建方案．
【素材1】图1为某公交车停靠站，顶棚截面由若干段形状相同的抛物线拼接而成．图2为某段结构示意图，，皆为轴对称图形，且关于点成中心对称，该段结构水平宽度为8米．
【素材2】图3为停靠站部分截面示意图，两根长为2.5米的立柱，竖直立于地面并支撑在对称中心，处．小温将长为2.8米的竹竿竖直立于地面，当点触碰到顶棚时，测得为1米．
【素材3】将顶棚扩建，要求截面为轴对称图形，且水平宽度为27米．计划在顶棚两个末端到地面之间加装垂直于地面的挡风板．
【任务】
（1）确定中心：求图2中点到该结构最低点的水平距离．
（2）确定形状：在图3中建立合适的直角坐标系，求的函数表达式．
（3）确定高度：求挡风板的高度．
【答案】（1）2米 （2）见解析
（3）2.675m或2.325m
【解析】
【分析】本题考查了用待定系数法求函数的解析式、二次函数的图象和性质，根据题意建立适当的平面直角坐标系是解题的关键．
（1）根据对称性求解即可；
（2）以点为原点，按如图形式建立直角坐标系，由条件可求对称轴为，设顶点式为，把、代入求解即可；
（3）把，分别代入（2）中解析式求解即可．
【小问1详解】
解：由中心对称性得：米，由轴对称性得：米．
即图2中点到该结构最低点的水平距离为2米；
【小问2详解】
解：以点为原点，按如图形式建立直角坐标系，
由条件得，过、，对称轴为，
设顶点式为，
将、代入得，
解得：，，
；
【小问3详解】
解：，
（图3）
情况①：当时，，
情况②：将时，，
综上，挡风板的高度为2.675m或2.325m．次数
第1次
第2次
第3次
颜色
红球
红球
小温
小州