



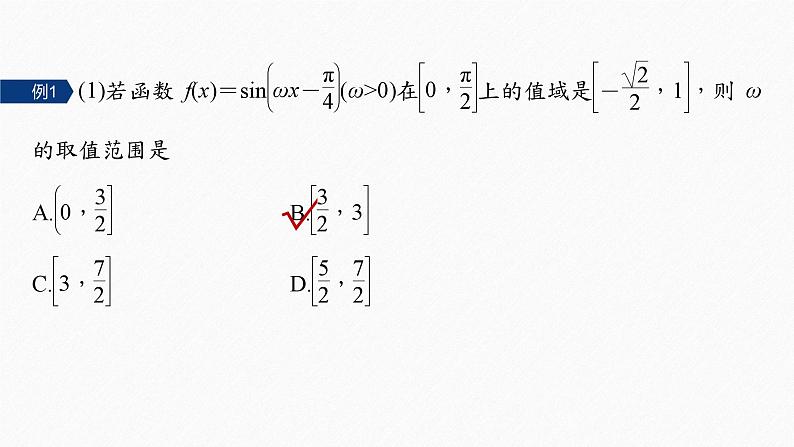







专题二 微重点3 三角函数中ω,φ的范围问题 2024年高考数学大二轮复习课件(含讲义)
展开三角函数中ω,φ的范围问题,是高考的重点和热点,主要考查由三角函数的最值(值域)、单调性、零点等求ω,φ的取值范围,难度中等偏上.
三角函数的最值(值域)与ω,φ的取值范围
单调性与ω,φ的取值范围
零点与ω,φ的取值范围
求三角函数的最值(值域)问题,主要是整体代换ωx±φ,利用正、余弦函数的图象求解,要注意自变量的范围.
其图象与直线y=3相邻两个交点的距离为π,
所以ω的最小值为11.
若三角函数在区间[a,b]上单调递增,则区间[a,b]是该函数单调递增区间的子集,利用集合的包含关系即可求解.
(1)(2023·新高考全国Ⅰ)已知函数f(x)=cs ωx-1(ω>0)在区间[0,2π]上有且仅有3个零点,则ω的取值范围是________.
因为0≤x≤2π,所以0≤ωx≤2ωπ,令f(x)=cs ωx-1=0,则cs ωx=1有3个根,令t=ωx,则cs t=1有3个根,其中t∈[0,2ωπ],结合余弦函数y=cs t的图象性质可得4π≤2ωπ<6π,故2≤ω<3.
已知函数的零点、极值点求ω,φ的取值范围问题,一是利用三角函数的图象求解;二是利用解析式,直接求函数的零点、极值点即可,注意函数的极值点即为三角函数的最大值、最小值点.
由上分析知,极值点个数可能为5或6个,B错误;
又因为f(x)在[-t,t]上单调递增,
即ω=6k1或ω=6k2+2,其中k1,k2∈Z,由于ω>0,所以ω的最小值为2.
由题意若f(x)的图象与直线y=-1在[0,2π]上有且仅有1个交点,
即f(x)在[0,2π]上可能有2个零点,也可能有3个或4个零点,B错误;
要使φ最小,则k取0,
2024年新高考数学第一轮复习课件:微专题6 三角函数中ω的范围问题: 这是一份2024年新高考数学第一轮复习课件:微专题6 三角函数中ω的范围问题,共14页。PPT课件主要包含了答案B,ACD,答案BD等内容,欢迎下载使用。
2024年新高考数学第一轮复习课件:微专题6 三角函数中ω的范围问题: 这是一份2024年新高考数学第一轮复习课件:微专题6 三角函数中ω的范围问题,共14页。
新高考版高考数学二轮复习(新高考版) 第1部分 专题突破 专题2 微重点6 三角函数中ω,φ的范围问题课件PPT: 这是一份新高考版高考数学二轮复习(新高考版) 第1部分 专题突破 专题2 微重点6 三角函数中ω,φ的范围问题课件PPT,共59页。PPT课件主要包含了专题强化练等内容,欢迎下载使用。












