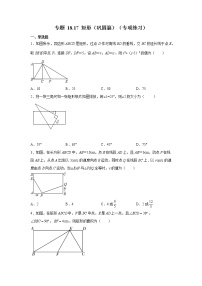
初中数学人教版八年级下册17.1 勾股定理随堂练习题

这是一份初中数学人教版八年级下册17.1 勾股定理随堂练习题，共28页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

1．《九章算术》是我国古代数学的重要著作，其中有一道题，原文是：今有户不知高、广，从之不出二尺，斜之适出，不知其高、宽，有竿，竿比门宽长出4尺；竖放；斜放，竿与门对角线恰好相等问．问门高、宽、对角线长分别是多少？若设门对角线长为x尺，则可列方程（ ）
A．x2＝（x﹣4）2＋（x﹣2）2B．2x2＝（x﹣4）2＋（x﹣2）2
C．x2＝42＋（x﹣2）2D．x2＝（x﹣4）2＋22
2．如图，在长方体盒子上有一只蚂蚁从顶点出发，要爬行到顶点去找食物，已知长方体的长、宽、高分别为4、1、2，则蚂蚁走的最短路径长为（ ）
A．B．5C．D．7
3．如图，沿AC方向开山修建一条公路,为了加快施工进度,要在小山的另一边寻找点E同时施工，从AC上的一点B取∠ABD=150°，沿BD的方向前进,取∠BDE=60°，测得BD=520 m,BC=80 m,并且AC、BD和DE在同一平面内，那么公路CE段的长度为( )
A．180mB．260mC．(260-80)mD．(260-80)m
4．如图，有一个水池，水面是一个边长为14尺的正方形，在水池正中央有一根芦苇，它高出水面1尺，如果把这根芦苇拉向水池一边的中点，它的顶端恰好到达池边的水面．则水的深度是（ ）
A．15尺B．24尺C．25尺D．28尺
5．如图是楼梯的一部分，若，，，一只蚂蚁在A处发现C处有一块糖，则这只蚂蚁吃到糖所走的最短路程为（ ）
A．B．3C．D．
6．如图，高速公路上有A、B两点相距25km，C、D为两村庄，已知DA＝10km，CB＝15km．DA⊥AB于A，CB⊥AB于B，现要在AB上建一个服务站E，使得C、D两村庄到E站的距离相等，则AE的长是（ ）km．
A．5B．10C．15D．25
7．如图，已知中，，F是高和的交点，，，则线段的长度为（ ）
A．B．2C．D．1
8．如图，在中，，按以下步骤作图：①以为圆心，任意长为半径作弧，分别交、于、两点；②分别以、为圆心，以大于的长为半径作弧，两弧相交于点；③作射线，交边于点．若，，则线段的长为（ ）
A．3B．C．D．
9．如图甲，直角三角形的三边a，b，c，满足的关系．利用这个关系，探究下面的问题：如图乙，是腰长为1的等腰直角三角形，，延长至，使，以为底，在外侧作等腰直角三角形，再延长至，使，以为底，在外侧作等腰直角三角形，……，按此规律作等腰直角三角形（，n为正整数），则的长及的面积分别是（ ）
A．2，B．4，C．，D．2，
10．如图，桌上有一个圆柱形玻璃杯（无盖）高6厘米，底面周长16厘米，在杯口内壁离杯口1.5厘米的A处有一滴蜜糖，在玻璃杯的外壁，A的相对方向有一小虫P，小虫离杯底的垂直距离为1.5厘米，小虫爬到蜜糖处的最短距离是（ ）
A．厘米B．10厘米C．厘米D．8厘米
二、填空题
11．如图，在离水面高度为8米的岸上，有人用绳子拉船靠岸，开始时绳子BC的长为17米，几分钟后船到达点D的位置，此时绳子CD的长为10米，问船向岸边移动了__米．
12．我国古代数学名著《算法统宗》有一道“荡秋千”的问题：“平地秋千未起，踏板一尺离地．送行二步与人齐，5尺人高曾记，仕女家人争蹴．良工高士素好奇，算出索长有几？”此问题可理解为：“如图，有一架秋千，当它静止时，踏板离地距离的长为1尺，将它向前水平推送10尺时，即尺，秋千踏板离地的距离和身高5尺的人一样高，秋千的绳索始终拉得很直，试问绳索有多长？”，设秋千的绳索长为x尺，根据题意可列方程为___________．
13．如图，海中有一个小岛A，一艘轮船由西向东航行，在点处测得小岛A在它的北偏东方向上，航行12海里到达点处，测得小岛A在它的北偏东方向上，那么小岛A到航线的距离等于____________海里．
14．如图，在高2米，坡角为30°的楼梯表面铺地毯，地毯的长至少需______米．
15．如图，一个长方体盒子紧贴地面，一只蚂蚁由出发，在盒子表面上爬到点，已知，，，这只蚂蚁爬行的最短路程是________．
16．如图，商场（点M）距公路（直线l）的距离（MA）为3km，在公路上有一车站（点N），车站距商场（NM）为4km，公交公司拟在公路上建一个公交车站停靠站（点P），要求停靠站到商场与到车站的距离相等，则停靠站到车站的距离（NP）的长为_____．
17．如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝4，点E在AC上，且AE＝1，连接BE，∠BEF＝90°，且BE＝FE，连接CF，则CF的长为____________
18．如图，AB⊥BC于点B，AB⊥AD于点A，点E是CD中点，若BC＝5，AD＝10，BE＝，则AB的长是 _____．
三、解答题
19．中国机器人创意大赛于2014年7月15日在哈尔滨开幕．如图是一参赛队员设计的机器人比赛时行走的路径，机器人从A处先往东走4m，又往北走1.5m，遇到障碍后又往西走2m，再转向北走4.5m处往东一拐，仅走0.5m就到达了B．问机器人从点A到点B之间的距离是多少？
20．如图，在平静的湖面上有一支红莲BA，高出水面的部分AC为0.5米，一阵风吹来，红莲被吹到一边，花朵齐及水面（即），已知红莲移动的水平距离CD为2米，则湖水深CB为多少？
21．台风是一种自然灾害，它以台风中心为圆心在周围上百千米的范围内形成极端气候，有极强的破坏力，如图，有一台风中心沿东西方向由行驶向，已知点为一海港，且点与直线上的两点，的距离分别为，，又，以台风中心为圆心周围以内为受影响区域．
（1）求的度数．
（2）海港受台风影响吗？为什么？
（3）若台风的速度为千米/小时，当台风运动到点处时，海港刚好受到影响，当台风运动到点时，海港刚好不受影响，即，则台风影响该海港持续的时间有多长？
22．如图，在等边△ABC中，D是CB延长线上一点，E是AD上一点，且AE＝AB，EB、AC的延长线相交于点F．
求证：∠D＝2∠F；
探究线段AD、BD、CF的数量关系，并说明理由；
若DE＝4，CF＝12，求BD的长．
23．如图，在平面直角坐标系中，点，，且，，以为腰作等腰，，点为的中点，直线轴，交轴于点，交的延长线于点．
求证：；
若，试探究a，b之间的关系式；
在（2）的条件下，当时，求三角形的面积．
24．（1）已知如图，在中，，，，，求的长．
（2）【拓展】已知在中，，，．
（如图）（一），求的长．可以运用“等面积法”解答如下：
解：∵，
∴，
①如图（二），在斜边上有一点，，；若，则的长为________．
②如图（三），在内有一点，，，，若，则的长为________．
参考答案
1．A
【分析】根据题中所给的条件可知，竿斜放就恰好等于门的对角线长，可与门的宽和高构成直角三角形，运用勾股定理可求出门高、宽、对角线长．
解：根据勾股定理可得：
x2=（x-4）2+（x-2）2，
故选：A．
【点拨】本题考查勾股定理的运用，正确运用勾股定理，将数学思想运用到实际问题中是解答本题的关键，难度一般．
2．B
【分析】如图（见分析），根据长方体的展开图分三种情况讨论，然后分别利用勾股定理求解即可得．
解：根据长方体的展开图，分以下三种情况：
（1）如图1，最短路径；
（2）如图2，最短路径；
（3）如图3，最短路径；
因为，
所以蚂蚁走的最短路径长为5，
故选：B．
【点拨】本题考查了勾股定理的应用，根据长方体的展开图分情况讨论是解题关键．
3．C
【分析】由已知可求得∠DBE=180°-∠ABD=30°，∠E=90°，继而根据可求出DE的长，然后根据勾股定理可求出BE的长，继而可求出CE的长.
解：∵∠ABD是△BDE的外角，∠ABD=150°，∠D=60°，
∴∠DBE=180°-∠ABD=30°，∠E=150°-60°=90°，
∴DE=BD=×520=260，
∴BE==260（m），
∴公路CE段的长度为(260-80)（m），
故选：C．
【点拨】本题考查了勾股定理的应用，熟练掌握勾股定理以及含30度角的直角三角形的性质是解题的关键.
4．B
【分析】根据题意，可知EB'的长为14尺，则尺，设出尺，表示出水深AC，根据勾股定理建立方程即可．
解：依题意画出图形，
设芦苇长尺，则水深尺，因为尺，所以尺，
在Rt△AB'C中，∵，
∴，
解得：，
∴水深为：尺，
故选：B．
【点拨】本题考查了勾股定理的应用，正方形的性质等知识，熟悉数形结合的解题思想是解题关键．
5．D
【分析】此类题目只需要将其展开便可直观的得出解题思路．将台阶展开得到的是一个矩形，蚂蚁要从A点到C点的最短距离，便是矩形的对角线，利用勾股定理即可解出答案．
解：将台阶展开，如图，
因为DC=AE+BE=3+1=4，AD=2，
所以AC2=DC2+AD2=20，
所以AC=，
故选：D．
【点拨】本题考查了平面展开-最短路径问题，用到台阶的平面展开图，根据题意判断出长方形的长和宽是解题的关键．
6．C
【分析】根据题意设出AE的长为x，再由勾股定理列出方程求解即可．
解：设AE＝x，则BE＝25﹣x，
由勾股定理得：
在Rt△ADE中，
DE2＝AD2+AE2＝102+x2，
在Rt△BCE中，
CE2＝BC2+BE2＝152+（25﹣x）2，
由题意可知：DE＝CE，
所以：102+x2＝152+（25﹣x）2，
解得：x＝15km．
所以，E应建在距A点15km处．
故选：C．
【点拨】本题考查正确运用勾股定理，善于观察题目的信息是解题以及学好数学的关键．
7．D
【分析】先证明△BDF≌△ADC，得到BF=AC=，再根据勾股定理即可求解．
解：∵和是△ABC的高线，
∴∠ADB=∠ADC=∠BEC=90°，
∴∠DBF+∠C=90°，∠CAD+∠C=90°，
∴∠DBF=∠CAD，
∵，
∴∠BAD=45°，
∴BD=AD，
∴△BDF≌△ADC，
∴BF=AC=，
在Rt△BDF中，DF=．
故选：D
【点拨】本题考查了全等三角形的判定与性质，勾股定理等知识，证明△BDF≌△ADC是解题关键．
8．A
【分析】由尺规作图痕迹可知，BD是∠ABC的角平分线，过D点作DH⊥AB于H点，根据全等证明出BC=BH,设DC=DH=x则AD=AC-DC=8-x，BC=BH=6，AH=AB-BH=4，在Rt△ADH中，由勾股定理得到 ，由此即可求出x的值．
解：由尺规作图痕迹可知，BD是∠ABC的角平分线，
过D点作DH⊥AB于H点，
∵∠C=∠DHB=90°，
∴DC=DH，
，
∵∠C=∠DHB=90°，∠HBD=∠CBD，BD=BD
∴△BHD≌△BCD（AAS）
∴ BC=BH
设DC=DH=x，则AD=AC-DC=8-x，BC=BH=6，AH=AB-BH=4，
在Rt△ADH中，由勾股定理：，
代入数据：，解得，故，
故选：A．
【点拨】本题考查了角平分线的尺规作图，在角的内部角平分线上的点到角两边的距离相等，勾股定理等相关知识点，熟练掌握角平分线的尺规作图是解决本题的关键．
9．A
【分析】根据题意结合等腰直角三角形的性质，即可判断出的长，再进一步推出一般规律，利用规律求解的面积即可．
解：由题意可得：，，
∵为等腰直角三角形，且“直角三角形的三边a，b，c，满足的关系”，
∴根据题意可得：，
∴，
∴，
，
∴总结出，
∵，，，
∴归纳得出一般规律：，
∴，
故选：A．
【点拨】本题考查等腰直角三角形的性质，图形变化类的规律探究问题，立即题意并灵活运用等腰直角三角形的性质归纳一般规律是解题关键．
10．B
【分析】把圆柱沿着点A所在母线展开，把圆柱上最短距离转化为将军饮马河型最短问题求解即可.
解：把圆柱沿着点A所在母线展开，如图所示，
作点A的对称点B，
连接PB，
则PB为所求，
根据题意，得PC=8，BC=6，
根据勾股定理，得PB=10，
故选B.
【点拨】本题考查了圆柱上的最短问题，利用圆柱展开，把问题转化为将军饮马河问题，灵活使用勾股定理是解题的关键.
11．9．
【分析】在Rt△ABC中，利用勾股定理计算出AB长，再根据题意可得CD长，然后再次利用勾股定理计算出AD长，再利用BD=AB-AD可得BD长．
解：在Rt△ABC中：
∵∠CAB＝90°，BC＝17米，AC＝8米，
∴AB＝＝＝15（米），
∵CD＝10（米），
∴AD＝＝6（米），
∴BD＝AB﹣AD＝15﹣6＝9（米），
答：船向岸边移动了9米，
故答案为：9．
【点拨】本题考查了勾股定理的应用，关键是掌握从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．
12．（x+1﹣5）2+102＝x2．
【分析】根据勾股定理列方程即可得出结论．
解：由题意知：
OP'＝x，OC＝x+1﹣5，P'C＝10，
在Rt△OCP'中，由勾股定理得：
（x+1﹣5）2+102＝x2．
故答案为：（x+1﹣5）2+102＝x2．
【点拨】本题主要考查了勾股定理的应用和列方程，读懂题意是解题的关键．
13．
【分析】如图，过点A作AD⊥BC于D，根据题意可知∠EBA=60°，∠FCA=30°，EB⊥BC，FC⊥BC，可得∠ABD=30°，∠ACD=60°，∠CAD=30°，根据外角性质可得∠BAC=30°，可得AC=BC，根据含30°角的直角三角形的性质可得出CD的长，利用勾股定理即可求出AD的长，可得答案．
解：如图，过点A作AD⊥BC于D，
根据题意可知∠EBA=60°，∠FCA=30°，EB⊥BC，FC⊥BC，BC=12，
∴∠ABD=30°，∠ACD=60°，∠CAD=30°，
∴∠BAC=∠ACD-∠ABD=30°，
∴AC=BC=12，
∴CD=AC=6，
∴AD===．
故答案为：
【点拨】本题考查方向角的定义、三角形外角性质、含30°角的直角三角形的性质及勾股定理，三角形的一个外角，等于和它不相邻的两个内角的和；30°角所对的直角边，等于斜边的一半；熟练掌握相关性质及定义是解题关键．
14．2+2
【分析】地毯的竖直的线段加起来等于BC，水平的线段相加正好等于AC，即地毯的总长度至少为（AC+BC）．
解：
在Rt△ABC中，∠A=30°，BC=2m，∠C=90°，
∴AB=2BC=4m，
∴AC=m，
∴AC+BC=2+2（m）.
故答案为2+2.
【点拨】本题主要考查勾股定理的应用，解此题的关键在于准确理解题中地毯的长度为水平与竖直的线段的和.
15．
【分析】将长方体盒子按不同方式展开，得到不同的长方形，求出不同长方形的对角线，最短者即为正确答案．
解：由题意，
如图所示，
得；
如图所示，
得，
如图3所示，
，
∴蚂蚁爬行的最短路程是10．
故答案为：10.
【解答】本题考查了勾股定理的应用，根据题意将长方体盒子展开为平面图形，根据勾股定理求出最短路程进行比较是解题关键．
16．km
【分析】首先在Rt△AMN中，求出AN，设PN=PM=x，在Rt△PAM中，利用勾股定理列出方程即可解决问题．
解：如图，
连接MP，在Rt△MAN中，MA=3，MN=4，
由勾股定理得，
设NP=xkm，则PM=xkm，
∴PA=（ -x）km，
在Rt△MAP中，由勾股定理得
，
解得．
故答案为：km
【点拨】本题考查勾股定理的应用，解题的关键是学会利用勾股定理构建方程解决问题．
17．.
【分析】过点F作FM⊥AC交AC延长线于M，根据∠BEF=90°且BE=EF，可以得到△EFM≌△BEC，从而可以计算出CM、FM的长，再利用勾股定理即可得到CF的长.
解：∵∠ACB＝90°，AC＝BC＝4，，AE＝1
∴CE＝3
∵FM⊥AC，∠BEF＝90°
∴∠ACB＝∠BEF =∠FME =90°
∴∠FEM+∠EFM=90°=∠BEC+∠FEM
∴∠EFM=∠BEC
又∵BE=FE
∴△EFM≌△BEC
∴BC＝EM＝4，CE＝FM＝3
∴CM=EM-EC=1
∴
故答案为：.
【点拨】此题主要考查了全等三角形的性质与判定，勾股定理的运用，解题的关键在于能够熟练掌握相关知识进行求解.
18．12
【分析】延长BE交AD于点F，由“ASA”可证△BCE≌△FDE，可得DF＝BC＝5，BE＝EF，由勾股定理可求AB的长．
解：如图，延长BE交AD于点F，
∵点E是DC的中点，
∴DE＝CE，
∵AB⊥BC，AB⊥AD，
∴AD∥BC，
∴∠ D＝∠BCE，∠FED＝∠BEC，
∴ △BCE≌△FDE（ASA），
∴DF＝BC＝5，BE＝EF，
∴BF＝2BE＝13，AF=5,
在Rt△ABF中，由勾股定理可得AB＝12．
故答案为：12．
【点拨】本题考查了全等三角形的判定和性质，勾股定理，添加恰当辅助线构造全等三角形是本题的关键．
19．
试题分析：过点B作BCAD于C，可以计算出AC、BC的长度，在直角△ABC中根据勾股定理即可计算AB．
解：过点B作BCAD于C，
所以AC=4﹣2+0．5=2．5m，BC=4．5+1．5=6m，
在直角△ABC中，AB为斜边，则m,
答：机器人从点A到点B之间的距离是m．
考点：勾股定理．
20．湖水深BC为米
【分析】直接利用勾股定理得出，进而求出答案．
解：设BC为米，
∵在中，，，，
∴由勾股定理得：，
即，
解得：，
∴湖水深BC为米．
【点拨】此题主要考查了勾股定理的应用，正确得出方程是解题关键．
21．（1）；（2）海港受台风影响，证明见分析；（3）台风影响该海港持续的时间为小时．
【分析】（1）根据勾股定理的逆定理进行判断；
（2）利用勾股定理的逆定理得出△ABC是直角三角形，进而利用三角形面积得出CD的长，进而得出海港C是否受台风影响；
（3）利用勾股定理得出ED以及EF的长，进而得出台风影响该海港持续的时间．
解：（1），，，
，
是直角三角形，
∴∠ACB=90°；
（2）海港受台风影响，
过点作，
是直角三角形，
，
，
，
以台风中心为圆心周围以内为受影响区域，
海港受台风影响．
（3）当，时，正好影响港口，
，
，
台风的速度为千米/小时，
（小时）
答：台风影响该海港持续的时间为小时．
【点拨】本题考查的是勾股定理在实际生活中的运用，解答此类题目的关键是构造出直角三角形，再利用勾股定理解答．
22．(1) 见分析(2) CF＝BD+AD，理由见分析(3) 5
【分析】（1）在CF上截取CT，使得CT=BD．利用SAS证明△ABD≌△BCT，推出∠D=∠CTB，∠DAB=∠CBT，再证明∠TBF=∠F可得结论．
（2）结论：CF=BD+AD．利用全等三角形的性质证明即可．
（3）过点T作TR⊥DC交DC的延长线于R．设BD=CT=x，AE=BC=AC=AB=y，则AD=BT=TC=4+y，构建方程组求出x即可．
解：（1）证明：如图，在CF上截取CT，使得CT＝BD，连接BT．
∵△ABC是等边三角形，
∴AB＝BC，∠ABC＝∠ACB＝60°，
∴∠ABD＝∠BCT＝120°，
在△ABD和△BCT中，
，
∴△ABD≌△BCT（SAS），
∴∠D＝∠CTB，∠DAB＝∠CBT，
∵AE＝AB，
∴∠AEB＝∠ABE，
∵∠F+∠AEB+∠FAE＝180°，∠BAC＝60°，
∴∠F+∠AEB+∠EAB+60°＝180°，
∵∠TBF+∠CBT+∠ABC+∠ABE＝180°，
∴∠TBF+∠AEB+∠BAD+60°＝180°，
∴∠TBF＝∠F，
∵∠CTB＝∠TBF+∠F，
∴∠D＝2∠F．
（2）结论：CF＝BD+AD．
理由：由（1）可知，△ABD≌△BCT，
∴AD＝BT，
∵∠TBF＝∠F，
∴TB＝TF，
∵CF＝CT+TF，BD＝CT，
∴CF＝BD+AD．
（3）如图，在CF上截取CT，使得CT＝BD，连接BT．过点T作TR⊥DC交DC的延长线于R．
设BD＝CT＝x，AE＝BC＝AC＝AB＝y，则AD＝BT＝TC＝4+y，
在Rt△CTR中，∠R＝90°，∠TCR＝∠ACB＝60°，CT＝x，
∴CR＝x，TR＝x，
在Rt△BTR中，BT2＝BR2+RT2，
∴（4+y）2＝（y+x）2+（x）2，
又∵CF＝12，
∴x+4+y＝12，
∴y＝8﹣x，
∴（12﹣x）2＝（8﹣x+x）2+（x）2，
∴x＝5，
∴BD＝5．
【点拨】本题属于三角形综合题，考查了全等三角形的判定和性质，等边三角形的性质，等腰三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数构建方程组解决问题，属于中考压轴题．
23．(1) 见详解(2) (3)
【分析】（1）根据题意可得，再证明，可得，，从而得到，然后根据，可得，从而得到，即可；
（2）根据，即可求解；
（3）根据，可得，再结合（2）中的结论，可得，即可求解．
（1）解：∵点，，且，，
∴，
是等腰直角三角形，
，
，
，
，，
，
，，
，
轴，
，，
点D是BC的中点，
，
，
，
，
；
（2）解：由（1）得： ，
∴，
∵在等腰中，，
∴，
即，
∴；
（3）由（1）得：，
轴，
∴，
∵，
∴，即，
∴，
∴，
∵，
∴，
∴，
∴．
【点拨】本题主要考查了等腰直角三角形的性质，全等三角形的判定和性质，完全平方公式的应用，坐标与图形，根据题意，证得全等三角形是解题的关键．
24．（1）；（2）①，②
【分析】（1）根据等面积法进行求解即可；
（2）①连接，运用等面积法可得的面积的面积的面积，设，进而计算即可；
②连接，运用等面积法可得的面积的面积的面积的面积，设，进而计算即可．
解：（1）在中，,
∴，
∴，
∴
（2）①连接，
∵的面积的面积的面积，
∴，
设，
∴，
解得，
∴，
故答案为：；
②连接，
∵的面积的面积的面积的面积，
∴，
设，
∴，
解得，
∴，
故答案为：；
【点拨】本题考查了等面积法和一元一次方程的运用，灵活运用所学知识求解是解决本题的关键．