初中数学人教版八年级下册17.1 勾股定理课时练习

这是一份初中数学人教版八年级下册17.1 勾股定理课时练习，共22页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。

一、单选题
1．下列给出的四组数中，能构成直角三角形三边的一组是（ ）
A．，，B．，，C．，，D．，，
2．如图，在中，，若，则正方形和正方形的面积和为（ ）
A．150B．200C．225D．无法计算
3．直角三角形的边长分别为a，b，c，若a2＝9，b2＝16，那么c2的值是（ ）
A．5B．7C．25D．25或7
4．在中，，，、、的对边分别是、、，则下列结论错误的是（ ）
A．B．C．D．
5．在西方，人们称为毕达哥拉斯定理，在我国把它称为勾股定理，其具体内容指的是（ ）
A．如果直角三角形的两条直角边分别为a，b，斜边为c，那么a2+b2=c2
B．如果直角三角形的三边分别为a，b，c，那么a2+b2=c2
C．如果三角形的三边分别为a，b，c，那么a2+b2=c2
D．如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形是直角三角形
6．如图，是一扇高为2m，宽为1.5m的门框，童师傅有3块薄木板，尺寸如下：
①号木板长3 m，宽2.7 m；
②号木板长2.8 m，宽2.8 m；
③号木板长4 m，宽2.4 m．
可以从这扇门通过的木板是（ ）号．
A．②B．③C．②③D．都不能通过
7．如图，在矩形COED中，点D的坐标是，则CE的长是（ ）
A．3B．C．D．4
8．如图，一圆柱体的底面周长为10cm，高AB为12cm，BC是直径，一只蚂蚁从点A出发沿着圆柱的表面爬行到点C的最短路程为（ ）
A．17cmB．13cmC．12cmD．14cm
9．五根小木棒，其长度分别为7，15，20，24，25，现将它们摆成两个直角三角形，如图，其中正确的是（ ）
A． B． C．D．
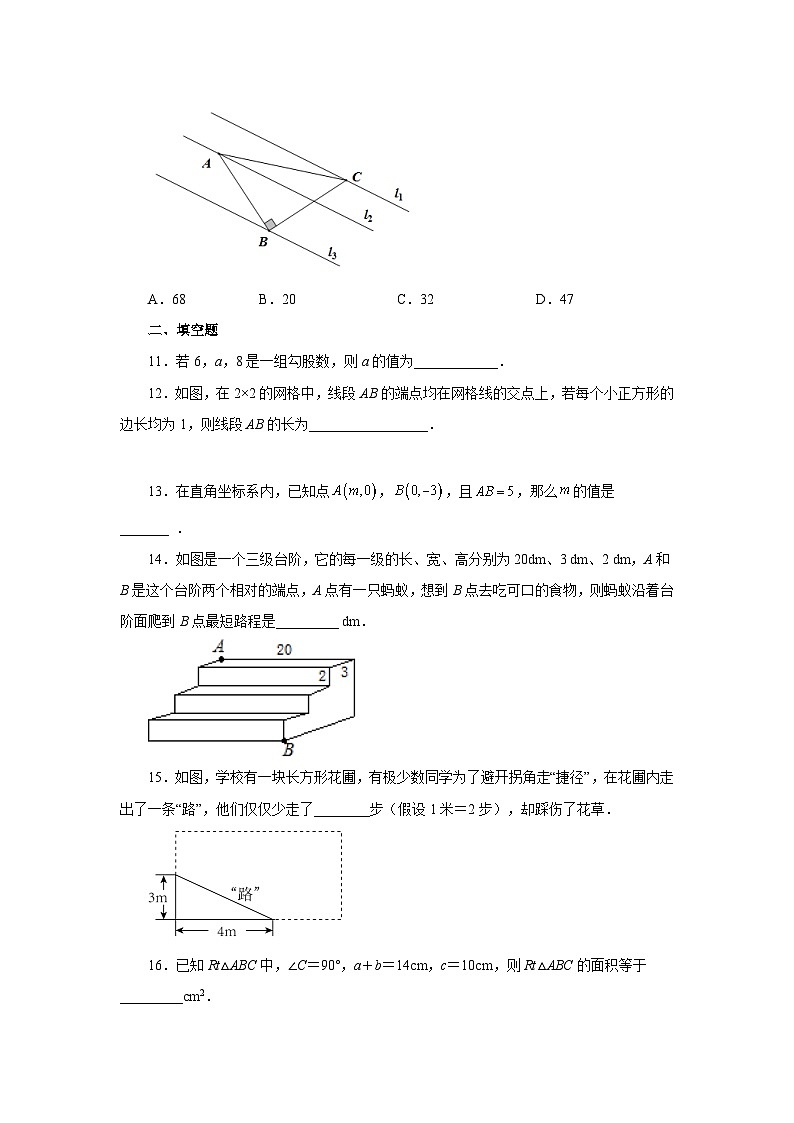
10．如图，已知△ABC中，∠ABC＝90°，AB＝BC，三角形的顶点在相互平行的三条直线，，上，且，之间的距离为2， ，之间的距离为3 ，则的值是（ ）
A．68B．20C．32D．47
二、填空题
11．若6，a，8是一组勾股数，则a的值为____________．
12．如图，在2×2的网格中，线段AB的端点均在网格线的交点上，若每个小正方形的边长均为1，则线段AB的长为_________________．
13．在直角坐标系内，已知点，，且，那么的值是_______ ．
14．如图是一个三级台阶，它的每一级的长、宽、高分别为20dm、3 dm、2 dm，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是_________ dm．
15．如图，学校有一块长方形花圃，有极少数同学为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了________步（假设1米＝2步），却踩伤了花草．
16．已知Rt△ABC中，∠C＝90°，a＋b＝14cm，c＝10cm，则Rt△ABC的面积等于_________cm2．
17．《九章算术》是我国古代最重要的数学著作之一，在“勾股”章中记载了一道“折竹抵地”问题：“今有竹高一丈，末折抵地，去本三尺，问折者高几何?”翻译成数学问题是：如图所示，中，∠ACB＝90°，AC＋AB＝10，BC＝3，求AC的长，如果设AC＝x，则可列方程为________（方程不用化简）．
18．如图，在中，，，D是AB的中点，点E、F分别在AC、BC边上运动点E不与点A、C重合，且保持，连接DE、DF、在此运动变化的过程中，有下列结论：；四边形CEDF的面积随点E、F位置的改变而发生变化；；以上结论正确的是______只填序号．
三、解答题
19．如图，在△ABC中，∠ACB为钝角．
尺规作图：在边AB上确定一点D，使∠ADC=2∠B（不写做法，保留作图痕迹，并标明字母）；
在（1）的条件下，若∠B=15°，CD=3，AC=，求△ABC的面积．
20．如图，，，．
求证：≌．
若，，，求的长．
21．勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，请你利用图1或图2证明勾股定理（其中∠DAB＝90°）
求证：a2+b2＝c2．
22．定义：在四边形中，如果，那么我们把这样的四边形称为余对角四边形．
{问题探索}问题：如图1，已知、是余对角四边形的对角线，，．求证：．
探索：小明同学通过观察、分析、思考，对上述问题形成了如下想法：
因为，，所以是等边三角形，将绕点顺时针方向旋转，得，连接．……请参考小明同学的想法，完成该问题的解答过程．
23．如图1，中，，
如图2，点是边上一点，沿着折叠，点恰好与斜边上点重合，求的长．
如图3，点为斜边上上动点，连接，在点的运动过程中，若为等腰三角形，请直接写出AF的长．
24．在Rt△ABC中，AB＝AC，∠CAB＝90°．点D是射线BA上一点，点E是线段AB上一点．且点D与点E关于直线AC对称，连接CD，过点E作直EF⊥CD于F，交CB的延长线于点G．
（1）根据题意补全图形；
（2）写出∠CDA与∠G之间的数量关系，并进行证明；
（3）已知在等腰直角三角形中，有以下结论：斜边长为一条直角边长的倍，写出线GB，AD之间的数量关系，并进行证明．
参考答案
1．C
【分析】根据勾股定理的逆定理即可求解．
解：、，不能构成直角三角形；
、，，不能构成直角三角形；
、，能构成直角三角形；
、，不能构成直角三角形．
故选：．
【点拨】本题主要考查勾股定理的逆定理判定直角三角形，掌握勾股定理逆定理的概念及运算是解题的关键．
2．C
【分析】根据勾股定理即可进行解答．
解：∵四边形和四边形为正方形，
∴， ，
∵在中，，
∴，
∴，
故选：C．
【点拨】本题主要考查了勾股定理，解题的关键是掌握直角三角形两直角边的平方和等于斜边的平方．
3．D
【分析】此题有两种情况：①当a，b为直角边，c为斜边，由勾股定理求出c2即可；②当a，c为直角边，b为斜边，利用勾股定理即可求解；即可得出结论．
解：当b为直角边时，c2＝a2+b2＝25，
当b为斜边时，c2＝b2﹣a2＝7，
故选D．
【点拨】此题主要考查学生对勾股定理的理解和掌握；解答此题要用分类讨论的思想，学生容易忽略a，c为直角边，b为斜边时这种情况，很容易选A，因此此题是一道易错题．
4．D
【分析】根据直角三角形的性质得到c＝2a，根据勾股定理计算，判断即可．
解：∵∠C＝90°，∠A＝30°，
∴c＝2a，A正确，不符合题意；
由勾股定理得，a2＋b2＝c2，B正确，不符合题意；
b＝＝a，即a：b＝1：，C正确，不符合题意；
∴b2＝3a2，D错误，符合题意，
故选：D．
【点拨】本题考查的是勾股定理、直角三角形的性质，直角三角形的两条直角边长分别是a，b，斜边长为c，那么a2＋b2＝c2．
5．A
【分析】根据勾股定理的内容，对选项逐个判断即可．
解：勾股定理的内容是：在直角三角形中，两条直角边的平方和等于斜边的平方，故A正确，符合题意；
B：没有指明直角边、斜边，故选项错误，不符合题意；
C：没有说明直角三角形，故选项错误，不符合题意；
D：勾股定理的逆定理，而不是勾股定理，故选项错误，不符合题意；
故选A．
【点拨】此题考查了勾股定理的基础知识，熟练掌握理解勾股定理的内容是解题的关键．
6．B
【分析】根据勾股定理，先计算出能通过的最大距离，然后和题中数据相比较即可．
解：因为，所以木板的长和宽中必须有一个数据小于2.5米．所以选③号木板．
故选：B．
【点拨】本题考查的是勾股定理的应用，掌握在Rt△ABC中，两直角边的平方和等于斜边的平方是解题的关键．
7．C
【分析】根据勾股定理求得，然后根据矩形的性质得出．
解：∵四边形COED是矩形，
∴CE=OD，
∵点D的坐标是（1，3），
∴，
∴，
故选C．
【点拨】本题考查了矩形的性质以及勾股定理的应用，熟练掌握矩形的性质是解题的关键．
8．B
【分析】将圆柱的侧面展开，得到一个长方形，再然后利用两点之间线段最短解答．
解：如图所示：
由于圆柱体的底面周长为10cm，
则AD=10×=5（cm）．
又因为CD=AB=12cm，
所以AC=＝13（cm）．
故蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是13cm．
故选：B．
【点拨】此题主要考查了平面展开图的最短路径问题，将圆柱的侧面展开，构造出直角三角形是解题的关键．
9．C
【分析】欲求证是否为直角三角形，这里给出三边的长，只要验证两小边的平方和等于最长边的平方即可．
解：A、，，，故A不正确，不符合题意；
B、，，故B不正确，不符合题意；
C、，，故C正确，符合题意；
D、，，故D不正确，不符合题意．
故选：C．
【点拨】本题考查了勾股定理逆定理，熟练掌握勾股定理是解本题的关键．
10．A
【分析】过A、C点作l3的垂线构造出直角三角形，根据三角形全等求出BE＝AD＝3，再由勾股定理求出BC的长，再利用勾股定理即可求出AC的长，最后得到AC2.
解：如图所示，过A作AD⊥l3于D，过C作CE⊥l3于E，
∵∠ABC=90°，
∴∠ABD+∠CBE=90°，
又∠DAB+∠ ABD=90°，
∴∠BAD=∠CBE，
在△ABD和△BEC中，
，
∴△ABD≌△BCE （AAS）
∴BE=AD=3，
在Rt△BCE中，根据勾股定理，得，
在Rt△ABC中，根据勾股定理，得 .
故答案是68.
【点拨】本题考查了全等三角形的性质和判定，勾股定理的应用，此题要作出平行线间的距离，构造直角三角形，运用全等三角形的判定和性质以及勾股定理进行计算.
11．10
【分析】分两种情况讨论：当a最大时，当8最大时，即可求解．
解：当a最大时，，
当8最大时， ，不是正整数，
所以a的值为10．
故答案为：10
【点拨】本题主要考查了勾股数，熟练掌握可以构成一个直角三角形三边的一组正整数，称之为勾股数是解题的关键．
12．
【分析】利用勾股定理即可计算．
解：根据题意，利用勾股定理有，
故答案为：．
【点拨】本题考查了勾股定理的的知识，通过网格点找到合适的直角三角形并确定其边长是解答本题的关键．
13．
【分析】结合两点间的距离公式根据的长列等式，计算可求解的值．
解：∵、，
∴，
∵，
∴，
解得，
故答案为：．
【点拨】本题主要考查两点间的距离公式，掌握两点间的距离公式是解题的关键．
14．25
【分析】把立体几何图展开得到平面几何图，如图，然后利用勾股定理计算AB，则根据两点之间线段最短得到蚂蚁所走的最短路线长度．
解：展开图为：
则AC=20dm,BC=3×3+2×3=15（dm）,
在Rt△ABC中， （dm）.
所以蚂蚁所走的最短路线长度为25 dm.
故答案为：25．
【点拨】本题考查了勾股定理的应用，把立体几何图中的问题转化为平面几何图中的问题是解题的关键．
15．4
【分析】根据勾股定理求出“路”的长度，再根据少走的“路”计算出少走的长度，得出所需步数即可．
解：由勾股定理可得：“路”的长度，
∴，
∵1米＝2步，
∴少走了4步
故答案为：4．
【点拨】本题主要考查了勾股定理的运用，熟练掌握相关概念是解题关键．
16．24
【分析】利用勾股定理，可得：a2+b2＝c2＝100，即（a+b）2﹣2ab＝100，可得ab＝48，即可得出面积．
解：∵∠C＝90°，
∴a2+b2＝c2＝100，
∴（a+b）2﹣2ab＝100，
∴196﹣2ab＝100，
∴ab＝48，
∴S△ABC＝＝24cm2；
故答案为：24．
【点拨】本题考查勾股定理、完全平方公式的变形求值、三角形面积计算的运用，熟知勾股定理是解题的关键．
17．
【分析】设AC=x，则AB=10-x，再由即可列出方程．
解：∵，且，
∴，
在Rt△ABC中，由勾股定理有：，
即：，
故可列出的方程为：，
故答案为：．
【点拨】本题考查了勾股定理的应用，熟练掌握勾股定理是解决本题的关键．
18．
【分析】连接CD证明，利用全等三角形的性质一一判断即可．
解：连接CD，
∵△ABC是等腰直角三角形，D是AB的中点，
∴ ，CD⊥AB，
又∵，
∴ ∠ADE=∠CDF=90°-∠EDC，
在△ADE和△CDF中， ，
∴（ASA）
∴ ED=DF，故①正确；
∴ ，
定值，故②错误，
∵，
∴ AE=CF，
∴，故③正确，
∵ AE=CF，AC=BC，
∴ EC=BF，
∴ ，
∵ ，
∴ ，故④正确．
故答案为①③④．
【点拨】本题考查全等三角形的判定和性质，勾股定理，等腰直角三角形的性质，解题的关键是正确寻找全等三角形解决问题．
19．(1) 见分析(2)
【分析】（1）作BC和垂直平分线，交AB于D，即可；
（2）过点C作CE⊥AB于点E，利用含30度角的直角三角形的性质以及勾股定理先后求得CE、DE、AE的长，再利用三角形的面积公式即可求解．
（1）解：如图，点D为所作；
根据垂直平分平分线的性质，知：CD=DB，
∴∠DCB=∠B，
∴∠ADC=∠DCB+∠B=2∠B；
（2）解：由（1）知∠ADC=2∠B，CD=DB，
过点C作CE⊥AB于点E，
∵∠B=15°，
∴∠ADC=2∠B=30°，
∵CD=3，
∴CD=DB=3，CE=CD=，
∴DE=，
∵AC=，
∴AE=，
∴AB=AE+ED+DB=，
∴△ABC的面积= ．
【点拨】本题考查了基本作图以及线段垂直平分线的性质、含30度角的直角三角形的性质、勾股定理等，充分发挥基本图形的作用，利用线段垂直平分线的性质求解．
20．(1)证明见分析
(2)
【分析】由全等三角形的判定定理证得≌；
由全等三角形的性质得出，由勾股定理可求出答案．
解：（1）证明：∵，
∴，
∴．
在与中，
，
∴≌；
（2）解：∵≌，
∴，
∵，，
∴．
【点拨】本题考查了全等三角形的判定与性质，勾股定理，证明≌是解题的关键．
21．见分析.
【分析】图1，根据三个直角三角形的面积和等于梯形的面积列式化简即可得证；
图2，连结DB，过点D作BC边上的高DF，则DF＝EC＝b﹣a，表示出S四边形ADCB＝S△ACD+S△ABC，S四边形ADCB＝S△ADB+S△DCB，两者相等，整理即可得证．
解：利用图1进行证明：
证明：∵∠DAB＝90°，点C，A，E在一条直线上，BC∥DE，则CE＝a+b，
∵S四边形BCED＝S△ABC+S△ABD+S△AED＝ab+c2+ab，
又∵S四边形BCED＝（a+b）2，
∴ab+c2+ab＝（a+b）2，
∴a2+b2＝c2．
利用图2进行证明：
证明：如图，连结DB，过点D作BC边上的高DF，则DF＝EC＝b﹣a，∵S四边形ADCB＝S△ACD+S△ABC＝b2+ab．
又∵S四边形ADCB＝S△ADB+S△DCB＝c2+a（b﹣a），
∴b2+ab＝c2+a（b﹣a），
∴a2+b2＝c2．
【点拨】本题考查勾股定理的证明，解题的关键是利用构图法来证明勾股定理.
22．证明过程见详解
【分析】是等边三角形，通过构造等边三角形，结合余对角四边形得出，在由勾股定理即可求解．
解：证明：∵，，
∴是等边三角形，
∵将绕点顺时针方向旋转，得，则，
∵，，，
∴，
∴，
∴为等边三角形，
∴，，
∵四边形为余对角四边形，
∴，
∴，
∴，
∴在中，，
又∵，，
∴，
故证明．
【点拨】本题主要考查等边三角形的变换问题，通过构造等边三角形，结合余对角四边形找出直角三角形，利用勾股定理即可求解，解题的关键在于将线条构造到直角三角形中．
23．(1) (2) 或
【分析】（1）设，则，根据折叠的性质得出，，在中，根据勾股定理列出方程，解方程即可求解；
（2）根据等腰三角形的定义，分类讨论，即可求解．
（1）解：设，则
∵，
∵沿着折叠，点恰好与斜边上点重合
∴，，
∴
在中，
∴
解得，
∴；
（2）解：∵是等腰三角形，
①，
∴，
②当时，如图，
∴，
又∵，
∴，
∴，
∴．
③∵点为斜边上上动点，所以不存在，
综上所述，或．
【点拨】本题考查了勾股定理，等腰三角形的定义，等腰三角形的判定，掌握分类讨论思想是解题的关键．
24．（1）见分析；（2）；（3），证明见分析
【分析】（1）根据题意画图即可；
（2）由直角三角形中，两个锐角互余，结合三角形的一个外角等于与其不相邻的两个内角的和解题即可；
（3）连接CE，过点G作GH，垂足为H，先证明CD=CE，由三线合一性质可知，并设，计算出，，继而证明EG=CE=CD，可证明，再由全等三角形的对应边相等，解得，最后结合勾股定理解题即可．
解：（1）如图：
（2）由图可知，
（3）连接CE，过点G作GH，垂足为H，
关于直线AC对称，
设
在中，
在中，，
EG=CE=CD
在与中
在中，
【点拨】本题考查几何变换综合题，其中涉及等腰直角三角形的性质、全等三角形的判定与性质、勾股定理、等腰三角形三线合一性质等知识，是重要考点，难度较易，作出适合的辅助线构造全等三角形，掌握相关知识是解题关键．