数学浙教版1.3平行线的判定优秀巩固练习

这是一份数学浙教版1.3平行线的判定优秀巩固练习，共11页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
一、选择题：本题共10小题，每小题3分，共30分。在每小题给出的选项中，只有一项是符合题目要求的。
1.已知在同一平面内有三条不同的直线a，b，c，下列说法中，错误的是
．( )
A. 如果a//b，a⊥c，那么b⊥cB. 如果b//a，c//a，那么b//c
C. 如果b⊥a，c⊥a，那么b⊥cD. 如果b⊥a，c⊥a，那么b//c
2.下列说法中，不正确的是( )
A. 同一平面内的两条直线不平行就相交
B. 同位角相等，两直线平行
C. 过直线外一点，只有一条直线与已知直线平行
D. 同位角互补，两直线平行
3.如图，直线a，b被直线c所截，下列条件中，能判定a/​/b的是( )
A. ∠2=∠4B. ∠1=∠2C. ∠5=∠2D. ∠3=∠4
4.【台州】如图，已知∠1=90°，为保证两条铁轨平行，添加的下列条件中，正确的是．( )
A. ∠2=90°B. ∠3=90°C. ∠4=90°D. ∠5=90°
5.【郴州】如图，直线a，b被直线c，d所截．下列条件能判定a//b的是
．( )
A. ∠1=∠3B. ∠2+∠4=180°C. ∠4=∠5D. ∠1=∠2
6.(2023·山东威海乳山期末)如图，下列条件无法判断AE//CD的是
．( )
A. ∠1=∠2B. ∠3=∠BCD
C. ∠4=∠5D. ∠AEC+∠DCB=180°
7.(2023·无锡滨湖期中)如图，给出下列条件：①∠1=∠2；②∠3=∠4；③AD//BE，且∠D=∠B；④AD//BE，且∠BAD=∠BCD.其中，能得出AB//DC的条件
( )
A. 只有①B. 只有②C. 只有②③D. 有②③④
8.(2023·湖北黄冈武穴期末)如图，下列不能判断AB//CD的条件有
．( )
①∠B+∠BAD=180°；②∠1=∠2；③∠3=∠4；④∠D=∠5．
A. 1个B. 2个C. 3个D. 4个
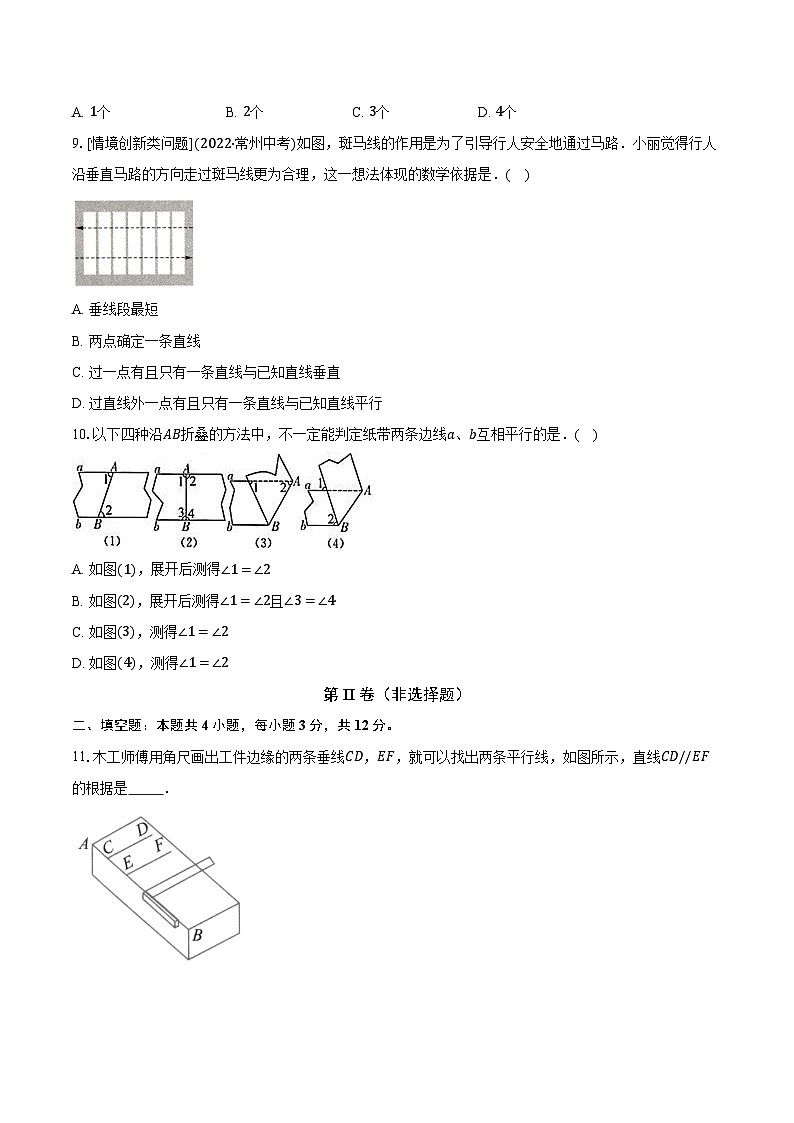
9.[情境创新类问题](2022·常州中考)如图，斑马线的作用是为了引导行人安全地通过马路．小丽觉得行人沿垂直马路的方向走过斑马线更为合理，这一想法体现的数学依据是．( )
A. 垂线段最短
B. 两点确定一条直线
C. 过一点有且只有一条直线与已知直线垂直
D. 过直线外一点有且只有一条直线与已知直线平行
10.以下四种沿AB折叠的方法中，不一定能判定纸带两条边线a、b互相平行的是．( )
A. 如图(1)，展开后测得∠1=∠2
B. 如图(2)，展开后测得∠1=∠2且∠3=∠4
C. 如图(3)，测得∠1=∠2
D. 如图(4)，测得∠1=∠2
第II卷（非选择题）
二、填空题：本题共4小题，每小题3分，共12分。
11.木工师傅用角尺画出工件边缘的两条垂线CD，EF，就可以找出两条平行线，如图所示，直线CD/​/EF的根据是 ．
12.我们学过用直尺和三角尺画平行线的方法，如图所示，直线a/​/b的根据是 ．
13.如图，将木条a，b，c钉在一起，∠1=50∘，∠2=70∘.当木条a按顺时针方向至少旋转 度时，a/​/b.
14.a，b，c为同一平面内三条不同的直线，若a⊥b，c⊥b，则a与c的位置关系是 ．
三、解答题：本题共6小题，共48分。解答应写出文字说明，证明过程或演算步骤。
15.(本小题8分)
如图，∠APB=Rt∠，顶点P在直线b上，一边与直线a交于点A，且∠1+∠2=90°.说明直线a // b的理由。
16.(本小题8分)
如图，BE平分∠ABD，DE平分∠BDC，∠1+∠2=90∘.判断直线AB，CD是否平行，并说明理由．
17.(本小题8分)
如图，已知∠1=30∘，∠B=60∘，AB⊥AC．
(1)∵AB⊥AC，∴∠BAC= ．
∵∠DAB+∠B=∠BAC+∠1+∠B= ，
∴ /​/ ．
(2) AB与CD平行吗?若平行，请说明理由;若不一定，则再加上一个什么条件，就可以说明它们互相平行?
18.(本小题8分)
如图，已知AB⊥BC，∠1+∠2=90∘，∠2=∠3.问：BE与DF平行吗?请说明理由．
19.(本小题8分)
如图，已知AB⊥BC，∠1+∠2=90∘，∠2=∠3.问：BE与DF平行吗?请说明理由．
20.(本小题8分)
如图，点A，D，B在同一条直线上，∠ADE=∠ABC，且DG，BF分别是∠ADE和∠ABC的角平分线.DG与BF平行吗?请说明理由．
答案和解析
1.【答案】C
【解析】【分析】
根据如果两条直线都与第三条直线平行，那么这两条直线也互相平行，同一平面内，垂直于同一条直线的两直线平行进行分析即可．
此题主要考查了平行公理及推论，关键是熟练掌握所学定理．
【解答】
解：A、如果a/​/b，a⊥c，那么b⊥c，说法正确；
B、如果b/​/a，c/​/a，那么b/​/c，说法正确；
C、如果b⊥a，c⊥a，那么b⊥c，应改为b/​/c，说法错误；
D、如果b⊥a，c⊥a，那么b/​/c，说法正确；
故选C．
2.【答案】D
【解析】略
3.【答案】A
【解析】略
4.【答案】C
【解析】【分析】
本题主要考查了平行线的判定，熟练掌握平行线的判定方法是解决问题的关键．
根据平行线的判定逐项分析即可得到结论．
【解答】
解：A.由∠2=90°不能判定两条铁轨平行，故该选项不符合题意；
B.由∠3=90°=∠1，可判定两枕木平行，故该选项不符合题意；
C.因为∠1=90°，∠4=90°，
所以∠1=∠4，
所以两条铁轨平行，故该选项符合题意；
D.由∠5=90°不能判定两条铁轨平行，故该选项不符合题意；
故选：C．
5.【答案】D
【解析】【分析】
此题主要考查了平行线的判定，正确掌握判定方法是解题关键．直接利用平行线的判定方法进而分析得出答案．
【解答】
解：A、当∠1=∠3时，c/​/d，故此选项不合题意；
B、当∠2+∠4=180°时，c/​/d，故此选项不合题意；
C、当∠4=∠5时，c/​/d，故此选项不合题意；
D、当∠1=∠2时，a/​/b，故此选项符合题意；
故选：D．
6.【答案】C
【解析】解：A、根据内错角相等，两直线平行，可以判断AE/​/CD，不符合题意；
B、根据同位角相等，两直线平行，可以判断AE/​/CD，不符合题意；
C、根据内错角相等，两直线平行，可以判断AD//BC，符合题意；
D、根据同旁内角互补，两直线平行，可以判断AE/​/CD，不符合题意．
故选：C．
根据平行线的判定逐一判断，即可得到答案．
本题考查了平行线的判定，熟练掌握平行线的判定方法和两个角的位置关系是解题关键．
7.【答案】D
【解析】【分析】
本题考查的是平行线的判定定理有关知识，根据平行线的判定定理分别进行分析即可．
利用平行线的判定方法判断即可得到正确的选项．
【解答】
解：①∵∠1=∠2，
∴AD//BC，本选项不合题意；
②∵∠3=∠4，∴AB/​/CD，本选项符合题意；
③∵AD//BE，∴∠BAD+∠B=180°，
∵∠D=∠B，
∴∠BAD+∠D=180°，
∴AB/​/CD，本选项符合题意；
④∵AD/​/BE，
∴∠BAD+∠B=180°，
∵∠BAD=∠BCD，
∴∠BCD+∠B=180°，
∴AB/​/CD，本选项符合题意，
则符合题意的选项为②③④．
故选D．
8.【答案】C
【解析】【分析】
本题考查了两直线平行的判定，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行，并要分清给出的角所截的是哪两条直线，根据平行线的判定定理，①，②，④不能判定AB/​/CD．
【解答】
解：因为∠B+∠BAD=180°，所以AD // BC(同旁内角互补，两直线平行)，故①不能判断AB // CD；
因为∠1=∠2，所以AD // BC(内错角相等，两直线平行)，故②不能判断AB // CD；
因为∠3=∠4，所以AB // CD(内错角相等，两直线平行)，故③能判断AB // CD；
因为∠D=∠5，所以AD // BC(内错角相等，两直线平行)，故④不能判断AB // CD．
故选C．
9.【答案】A
【解析】【分析】
本题主要考查了垂线段最短的性质，数学和生活密不可分，用数学的眼光去观察现实世界，将生活中的实际问题抽象成数学问题，再用所学知识去解决．
根据生活经验结合数学原理解答即可．
【解答】
解：小丽觉得行人沿垂直马路的方向走过斑马线更为合理，这一想法体现的数学依据是垂线段最短，
故选：A．
10.【答案】C
【解析】A.∵∠1=∠2，∴a//b，故该选项不符合题意；
B.∵∠1=∠2且∠3=∠4，∠1+∠2=180°，∠3+∠4=180°，∴∠1=∠2=∠3=∠4=90°，∴a//b，
故该选项不符合题意；
C.∵∠1与∠2既不是内错角也不是同位角，∴不一定能判定两直线平行，故该选项符合题意；
D.∵∠1=∠2，∴a//b，故该选项不符合题意．
故选C．
11.【答案】略
【解析】略
12.【答案】略
【解析】略
13.【答案】略
【解析】略
14.【答案】a/​/c
【解析】略
15.【答案】证明：法一：如图：
∵∠2+∠5=90°，∠1+∠2=90°，
∴∠1=∠5，
∴a/​/b；
法二：同上得出∠1=∠5，
∵∠1=∠4，
∴∠4=∠5，
∴a/​/b；
法三：∵∠1=∠5，∠1+∠3=180°，
∴∠3+∠5=180°，
∴a/​/b．
【解析】本题考查的是平行线的判定，用到的知识点为：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行．先根据∠2+∠5=90°，∠1+∠2=90°得出∠1=∠5，故可得出a/​/b；同理得出∠1=∠5，∠1=∠4，故∠4=∠5，故可得出a/​/b；先求出∠1=∠5，再由∠1+∠3=180°，所以∠3+∠5=180°，由此可得出a/​/b．
16.【答案】略
【解析】略
17.【答案】【小题1】
略
【小题2】
略

【解析】1. 略
2. 略
18.【答案】略
【解析】略
19.【答案】BE/​/DF，理由略
【解析】略
20.【答案】DG//BF.理由如下：由DG，BF分别是∠ADE和∠ABC的平分线，得∠ADG=12∠ADE，
∠ABF=12∠ABC，则∠ADG=∠ABF.由“同位角相等，两直线平行”，得DG//BF
【解析】略