专题13.10 期末复习之解答压轴题专项训练-2022-2023学年七年级数学下册举一反三系列（苏科版）

这是一份专题13.10 期末复习之解答压轴题专项训练-2022-2023学年七年级数学下册举一反三系列（苏科版），文件包含专题1310期末复习之解答压轴题专项训练苏科版原卷版docx、专题1310期末复习之解答压轴题专项训练苏科版解析版docx等2份试卷配套教学资源，其中试卷共104页， 欢迎下载使用。

考点1
平面图形的认识（二）解答期末真题压轴题
1．（2022春·江苏·七年级期末）汛期即将来临，防汛指挥部在某水域一危险地带两岸各安置了一探照灯，便于夜间查看河水及两岸河堤的情况．如图，灯A射出的光束自AM顺时针旋转至AN便立即回转，灯B射出的光束自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A射出的光束转动的速度是a°/秒，灯B射出的光束转动的速度是b°/秒，且a、b满足|a−3b|+(a+b−4)2=0．假定这一带水域两岸河堤是平行的，即PQ∥MN，且∠BAN=45°．
(1)求a、b的值；
(2)如图2，两灯同时转动，在灯A射出的光束到达AN之前，若两灯射出的光束交于点C，过C作CD⊥AC交PQ于点D，若∠BCD=20°，求∠BAC的度数；
(3)若灯B射线先转动30秒，灯A射出的光束才开始转动，在灯B射出的光束到达BQ之前，A灯转动几秒，两灯的光束互相平行？
【答案】(1)a=3，b=1
(2)30°
(3)当t=15秒或82.5秒时，两灯的光束互相平行．
【分析】（1）根据a−3b+a+b−42=0，可得a−3b=0，且a+b−4=0，进而得出a、b的值；
（2）设灯A射线转动时间为t秒，根据∠BCD=90°﹣∠BCA=90°−180°−2t=2t−90°=20°可得t的值，根据∠BAC=45°−180°−3t=3t−135°可得∠BAC；
（3）设A灯转动t秒，两灯的光束互相平行，分两种情况进行讨论：①在灯A射线转到AN之前，②在灯A射线转到AN之后，分别求得t的值即可．
【详解】（1）∵a−3b+a+b−42=0．
又∵a﹣3b≥0，a+b−42≥0．
∴a=3，b=1；
（2）设A灯转动时间为t秒，
如图，作CE//PQ，而PQ//MN,
∴PQ//CE//MN,
∴∠ACE=∠CAN=180°−3t°，∠BCE=∠CBD=t°，
∴∠BCA=∠CBD+∠CAN=t+180°−3t=180°−2t，
∵∠ACD=90°，
∴∠BCD=90°﹣∠BCA=90°−180°−2t=2t−90°=20°，
∴t=55°，
∵∠CAN=180°−3t，
∴∠BAC=45°−180°−3t=3t−135°=165°−135°=30°；
（3）设A灯转动t秒，两灯的光束互相平行．
依题意得0①当0解得t=15；
②当60解得t=82.5；
③当120解得t=195>150(不合题意)
综上所述，当t=15秒或82.5秒时，两灯的光束互相平行．
【点睛】本题主要考查了平行线的性质以及角的和差关系的运用，解决问题的关键是运用分类思想进行求解，解题时注意：两直线平行，内错角相等；两直线平行，同旁内角互补．
2．（2022春·江苏无锡·七年级校联考期末）如图，直线PQ∥MN，一副三角板（∠ABC=∠CDE=90°，∠ACB=30°，∠BAC=60°，∠DCE=∠DEC=45°）按如图①放置，其中点E在直线PQ上，点B，C均在直线MN上，且CE平分∠ACN．
(1)求∠DEQ的度数；
(2)如图②，若将△ABC绕B点以每秒5°的速度按逆时针方向旋转（A，C的对应点分别为F，G）．设旋转时间为t秒0≤t≤36；
①在旋转过程中，若边BG∥CD，求t的值；
②若在△ABC绕B点旋转的同时，△CDE绕E点以每秒4°的速度按顺时针方向旋转．请直接写出旋转过程中△CDE有一边与BG平行时t的值．
【答案】(1)60°
(2)①6；②103或703
【分析】（1）如图，先求解∠ACN=180°−∠ACB=150°，∠ECN=12∠ACN=75°，由PQ∥MN，可得∠QEC=180°−75°=105°，从而可得答案；
（2）①如图，由BG∥CD，可得∠GBC=∠DCN，可得∠GBC=30°，再列方程求解即可；②如图，当BG∥CD时，延长DC交MN于R．证明∠GBN=∠DRN，过D作DS∥PQ，则PQ∥DS∥MN，可得∠QED=60°+4t°，∠DRN=90°−60+4t°=30−4t°，再建立方程即可；如图中，当BG∥CD时，延长DC交NM于R．证明∠QED=60+4t°，∠DRM=90°−180°−60°−4t°=4t−30°，再建立方程求解即可．
【详解】（1）解：如图①中，
∵∠ACB=30°，
∴∠ACN=180°−∠ACB=150°，
∵CE平分∠ACN，
∴∠ECN=12∠ACN=75°，
∵PQ∥MN，
∴∠QEC=180°−75°=105°，
∴∠DEQ=∠QEC−∠CED=60°．
（2）①如图②中，
∵BG∥CD，
∴∠GBC=∠DCN，
∵∠DCN=∠ECN−∠ECD=75°−45°=30°，
∴∠GBC=30°，
∴5t=30，
∴t=6．
∴在旋转过程中，若边BG∥CD，t的值为6．
②如图③中，当BG∥CD时，延长DC交MN于R．
∵BG∥CD，
∴∠GBN=∠DRN，
过D作DS∥PQ，则PQ∥DS∥MN，
∴∠QED+∠DRN=∠EDS+∠RDS=∠EDR=90°，
∵∠QED=60°+4t°，
∴∠DRN=90°−60+4t°=30−4t°，
∴5t=30−4t，
∴t=103．
如图③﹣1中，当BG∥CD时，延长DC交NM于R．
∵BG∥CR，
∴∠GBN+∠DRM=180°，
∵∠QED=60+4t°，同理：∠EDR=∠PED+∠DRM，
∴∠DRM=90°−180°−60°−4t°=4t−30°，
∴5t+4t−30=180，
∴t=703．
综上所述，满足条件的t的值为103或703．
【点睛】本题考查的是平行公理的应用，平行线的性质，角平分线的含义，一元一次方程的应用，理解题意，利用数形结合，清晰的分类讨论都是解本题的关键．
3．（2022春·江苏·七年级期末）如图，已知直线AB∥CD，直线EF分别与AB，CD交于O点，G点．P点是直线EF上的一个动点．
(1)如图1，当P运动至AB与CD之间时，过点P作PM⊥PN分别交AB、CD于M、N．若∠BMP=14°，求∠PNG的度数；
(2)如图2，当点P运动至直线AB上方时，过点P作PM⊥PN分别交AB、CD于M、N．作∠EPM的角平分线并反向延长交AB于点T，交CD于点Q，作∠NPF的角平分线与CD交于点H，若∠PHC=70°，求∠BTQ的度数；
(3)过点P作PM⊥PN分别交AB、CD于M、N，设PN与AB交于点K，点O在MK之间，点M在点O的左边且MO∶KO=3∶1，S△POK=8．沿直线EF方向平移直线CD，并保持CD始终在AB下方，使得S△MOG=4．连接MG、MN、KG．请直接写出△MGN的面积．
【答案】(1)76°
(2)25°
(3)109或149
【分析】（1）作PQ∥AB，根据AB∥CD得PQ∥AB∥CD，即可得∠MPQ=∠PMB=14°，∠QPN=∠PNG，根据PM⊥PN得∠MPN=90°，即可得∠QPN=76°；
（2）根据角平分线的性质得∠RPE=∠RPM=12∠EPM ∠NPH=∠HPF=12∠NPF，根据PM⊥PN得∠MPN=90°，即可得∠EPM+∠NPF=90°，12∠EPM+12∠NPF=45°，则∠RPE=∠HPF=45°，根据∠RPE=∠QPG得∠QPG+∠HPF=45°，即∠HPQ=45°，根据三角形外角的性质可得∠PHC=∠HPQ+∠PQH，即∠PQH=25°，再根据AB∥CD，即可得；
（3）分情况讨论：①当点P在AB的下方时，连接KG、ON， 根据MO∶KO=3∶1，S△POK=8得S△POM=3S△POK=24，根据S△MOG=4，可得OP∶OG=24∶4=6∶1，则S△OKG=16S△POK=43，即可得S△PKG=S△POK−SOKG=203，根据OK∥GN，S△OKG=S△OKN=43，可得PK∶KN=S△POK∶S△OKN=6∶1，则S△KGN=16S△PKG=109，根据AB∥CD，即可得；②当点P在AB的上方时，连接KG、ON，同理，即可．
【详解】（1）解：如图1，作PQ∥AB，
∵AB∥CD，
∴PQ∥AB∥CD，
∴∠MPQ=∠PMB=14°，∠QPN=∠PNG，
∵PM⊥PN，
∴∠MPN=90°，
∴∠QPN=∠MPN−∠MPQ=90°−14°=76°，
∴∠PNG=∠QPN=76°；
（2）解：如图2，
∵RP平分∠EPM，
∴∠RPE=∠RPM=12∠EPM，
∵PH平分∠NPF，
∴∠NPAH=∠HPF=12∠NPF，
∵PM⊥PN，
∴∠MPN=90°，
∴∠EPM+∠NPF=90°，
∴12∠EPM+12∠NPF=45°，
∴∠RPE=∠HPF=45°，
∵∠RPE=∠QPG，
∴∠QPG+∠HPF=45°，
即∠HPQ=45°，
∵∠PHC是△PHQ的一个外角，且∠PHC=70°，
∴∠PHC=∠HPQ+∠PQH，
即∠PQH=∠PHC−∠HPQ=70°−45°=25°，
∵AB∥CD，
∴∠BTQ=∠PQH=25°；
（3）解：①如图4，当点P在AB的下方时，连接KG、ON，
∵MO:KO=3:1，S△POK=8，
∴S△POM=3S△POK=24，
∵S△MOG=4，
∴OP:OG=24:4=6:1，
∴S△OKG=16S△POK=43，
∴S△PKG=S△POK−SOKG=8−43=203，
∵OK∥GN，S△OKG=S△OKN=43，
∴PK:KN=S△POK:S△OKN=6:1，
∴S△KGN=16S△PKG=16×203=109，
∵AB∥CD，
∴S△MGN=S△KGN=109；
②如图5，当点P在AB的上方时，连接KG、ON，
∵MO∶KO=3∶1，S△POK=8，
∴S△POM=3S△POK=24，
∵S△MOG=4，
∴OP∶OG=24∶4=6∶1，
∴S△OKG=16S△POK=43，
∴S△PKG=S△POK+SOKG=8+43=283，
∵OK∥GN，S△OKG=S△OKN=43，
∴PK∶KN=S△POK∶S△OKN=6∶1，
∴S△KGN=16S△PKG=16×283=149；
∵AB∥CD，
∴S△MNG=S△GNK=149；
综上所述，△MGN的面积为109或149．
【点睛】本题属于几何变换综合题，考查了平行线的性质，角平分线的定义，三角形内角和定理，三角形的面积等知识，解题的关键是学会利用等高模型解决问题．
4．（2022春·江苏苏州·七年级统考期末）【理解概念】
（1）如果一条直线将一个图形分割成面积相等的两个部分，则称这条直线叫做该图形的“等积线”．
（2）如图①，直线l1∥l2，点A是直线l1上的一点，AB⊥l2，垂足为B，则线段AB的长度是l1与l2之间的距离．我们知道，两条平行线之间的距离处处相等．
【新知探究】
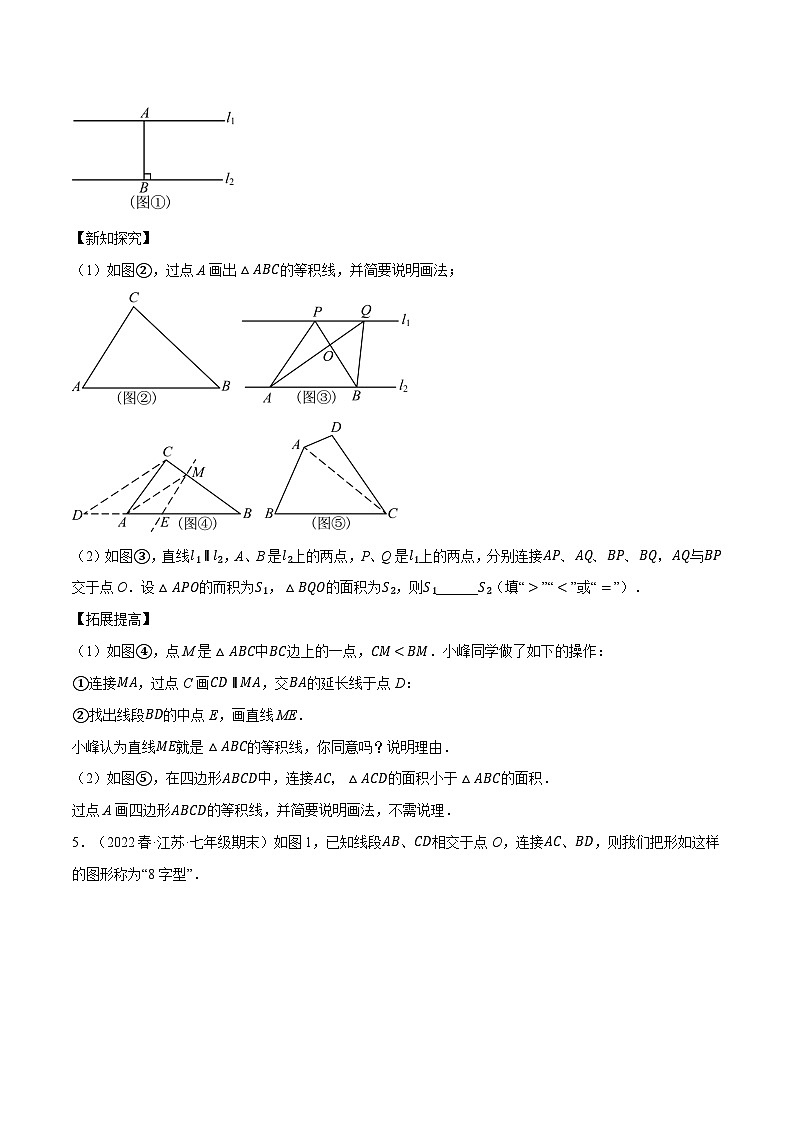
（1）如图②，过点A画出△ABC的等积线，并简要说明画法；
（2）如图③，直线l1∥l2，A、B是l2上的两点，P、Q是l1上的两点，分别连接AP、AQ、BP、BQ，AQ与BP交于点O．设△APO的而积为S1，△BQO的面积为S2，则S1______S2（填“>”“<”或“=”）．
【拓展提高】
（1）如图④，点M是△ABC中BC边上的一点，CM①连接MA，过点C画CD∥MA，交BA的延长线于点D：
②找出线段BD的中点E，画直线ME．
小峰认为直线ME就是△ABC的等积线，你同意吗？说明理由．
（2）如图⑤，在四边形ABCD中，连接AC，△ACD的面积小于△ABC的面积．
过点A画四边形ABCD的等积线，并简要说明画法，不需说理．
【答案】（1）见解析；（2）=；（1）同意，见解析；（2）见解析．
【分析】（1）三角形中线可将三角形面积平分，因此取中点连线即可；
（2）平行线中先找到面积相等的三角形，再减去相同的部分直接求出剩余部分面积相等即可；
（1）通过作辅助线得到S△MDA=S△AMC，然后推论出S△MBE=12S△MDB=12S△ABC，即可证明等积线；
（2）与（ 1）同理，推论出S△ADC=S△APC，然后取BP中点E，连接AE即可．
【详解】（1）取BC中点K，连接AK，AK是△ABC的等积线．
（2）∵l1∥l2，
∴S△APQ=S△BPQ，
∴S1=S2=S△APQ−S△POQ=S△BPQ−S△POQ，
故答案为：=；
（1）连接MD，
∵CD∥MA，
∴S△MDA=S△AMC，
∴S△ABC=S△MDB，
∵BD的中点是E，
∴S△MBE=12S△MDB=12S△ABC，
∴S△MEB=S四边形EMCA
∴ME就是△ABC的等积线．
（2）过D作DP∥AE交BC延长线于P，连接AP，
取BP中点E，连接AE，
与（1）同理可得，AE即为四边形ABCD的等积线．
【点睛】此题考查三角形中线的性质和平行线的性质，解题关键是在平行线中找出等面积的三角形进行转化．
5．（2022春·江苏·七年级期末）如图1，已知线段AB、CD相交于点O，连接AC、BD，则我们把形如这样的图形称为“8字型”．
(1)求证：∠A+∠C=∠B+∠D．
(2)如图2所示，∠1=130°，则∠A+∠B+∠C+∠D+∠E+∠F的度数为 ．
(3)如图3，若∠CAB和∠BDC的平分线AP和DP相交于点P，且与CD，AB分别相交于点M，N．
①若∠B=100°，∠C=120°，求∠P的度数．
②若角平分线中角的关系改成“∠CAP=14∠CAB， ∠CDP=14∠CDB”，试直接写出∠P与∠B，∠C之间存在的数量关系，并证明理由．
【答案】(1)见解析
(2)260°
(3)①110°；②4∠P=∠B+3∠C，理由见解析
【分析】（1）根据三角形的内角和即可得到结论；
（2）利用（1）的结论，结合三角形外角的性质即可求解；
（3）①根据角平分线的定义得到∠CAP=∠BAP，∠BDP=∠CDP，再根据三角形内角和定理得到∠CAP+∠C=∠CDP+∠P，∠BAP+∠P=∠BDP+∠B，两等式相减得到∠C−∠P=∠P−∠B，即∠P=12∠C+∠B，然后把∠C=120°，∠B=100°代入计算即可；
②与①的证明方法一样得到4∠P=∠B+3∠C．
【详解】（1）证明：在图1中，有∠A+∠C=180°−∠AOC，∠B+∠D=180°−∠BOD，
∵∠AOC=∠BOD，
∴∠A+∠C=∠B+∠D；
（2）解：如图2所示，
∵∠DME=∠A+∠E，∠3=∠DME+∠D，
∴∠A+∠E+∠D=∠3，
∵∠2=∠3+∠F，∠1=130°，
∴∠3+∠F=∠2=∠1=130°，
∴∠A+∠E+∠D+∠F=130°，
∵∠B+∠C=∠1=130°，
∴∠A+∠B+∠C+∠D+∠E+∠F=260°．
故答案为：260°．
（3）解①以M为交点“8字型”中，有∠P+∠CDP=∠C+∠CAP，
以N为交点“8字型”中，有∠P+∠BAP=∠B+∠BDP，
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP，
∵AP、DP分别平分∠CAB和∠BDC，
∴∠BAP=∠CAP，∠CDP=∠BDP，
∴2∠P=∠B+∠C，
∵∠B=100°，∠C=120°，
∴∠P=12∠B+∠C=110°；
②4∠P=∠B+3∠C，其理由是：
∵∠CAP=14∠CAB，∠CDP=14∠CDB，
∴∠BAP=34∠CAB，∠BDP=34∠CDB，
以M为交点“8字型”中，有∠P+∠CDP=∠C+∠CAP，
以N为交点“8字型”中，有∠P+∠BAP=∠B+∠BDP，
∴∠C−∠P=∠CDP−∠CAP=14∠CDB−∠CAB，
∠P−∠B=∠BDP−∠BAP=34∠CDB−∠CAB．
∴3∠C−∠P=∠P−∠B，
∴4∠P=∠B+3∠C．
【点睛】本题考查了三角形内角和定理：三角形内角和是180°，三角形外角的性质，角平分线的定义．明确题意，找出所求问题需要的条件是解题的关键．
6．（2022春·江苏南京·七年级校联考期末）如图，已知直线a // b，点A、E在直线a上，点B、F在直线b上，∠ABC＝100°，BD平分∠ABC交直线a于点D，线段EF在线段AB的左侧.若将线段EF沿射线 AD的方向平移，在平移的过程中BD所在的直线与 EF所在的直线交于点P．试探索 ∠1的度数与∠EPB的度数有怎样的关系？
为了解决以上问题，我们不妨从EF的某些特殊位置研究，最后再进行一般化.
【特殊化】
（1）如图，当∠1＝40°，且点P在直线a、b之间时，求∠EPB的度数；
（2）当∠1＝70 °时，求∠EPB的度数；
【一般化】
（3）当∠1＝n°时，求∠EPB的度数.（直接用含n的代数式表示）
【答案】（1）170°（2）见解析（3）①见解析②见解析
【分析】（1）作PG∥a，根据平行线性质和角平分线性质可得∠GPB=180°－12∠ABC=130°，计算即可；（2）作PG∥a，结合画图，分3种情况分析：当交点P在直线a上方，∠EPB＝20°；当交点P在直线a、b之间，∠EPB＝160°；当交点P在直线b下方，∠EPB＝20°；（3）根据（1）（2）情况，分2种情况分析：①当n＞50°时；②当n＜50°时，各有3种情况.
【详解】（1）作PG∥a，
∴∠EPG＝∠EFC=400
∵a∥b
∴PG∥b
∴∠GPB＋∠CBD=1800
又∵BD是∠ABC平分线，且∠ABC=1000，
∴∠GPB=1800－12∠ABC=1300
∴∠EPB＝∠EPG＋∠GPB=1700
（2）①当交点P在直线a上方，作PG∥a，
∵a∥b
∴PG∥b
∴∠EPG=∠1, ∠GPB=∠DBC
∴∠EPB＝700－500=200
②当交点P在直线a、b之间，作PG∥a，
∵a∥b
∴PG∥b
∴∠GPB=∠PBC=12∠ABC=500,∠BFE＝∠EPG=1800-∠1
∴∠EPB＝∠EPG＋∠GPB=500+1800-∠1=2300－700=1600
③当交点P在直线b下方，作PG∥a，
∵a∥b
∴PG∥b
∴∠EPG=∠1, ∠GPB=∠DBC
∴∠EPB＝700－500=200
（3）由（1）（2）得：①当n＞500时，
交点P在直线a上方，∠EPB＝n－500
交点P在直线a、b之间，∠EPB＝2300－n
交点P在直线b下方，∠EPB＝n－500
②当n＜500时，
交点P在直线a上方，∠EPB＝500－n
交点P在直线a、b之间，∠EPB＝1300＋n
交点P在直线b下方，∠EPB＝500－n
【点睛】考核知识点：平行线性质和判定的综合运用.作好辅助线，分类讨论是解决问题的关键.
7．（2022春·江苏盐城·七年级校考期末）【概念认识】
如图①，在∠ABC中，若∠ABD=∠DBE=∠EBC，则BD，BE叫做∠ABC的三分线．其中，BD是邻AB三分线，BE是邻BC三分线．
【问题解决】
(1)如图②，在△ABC中，∠ABC和外角∠ACD的三分线交于点E、F，若∠A=60°，求∠F的度数．
(2)如图③，若∠AOB=120°，射线OC在∠AOB内部，OM是∠AOC的邻OA三分线，ON是∠BOC的邻OB三分线，若OM、ON、OA、OB中有两条直线互相垂直时，求∠AOC．
【延伸推广】
(3)在（2）的条件下，若∠AOC<∠BOC时，射线ON以每秒1°的速度顺时针转动至OB便立刻回转，射线OM以每秒3°的速度顺时针转动至OB便立刻回转，然后在∠BOC间作往返运动，当ON第一次到达OC时，与射线OM同时停止转动，转动几秒后，OM，ON中，有一条射线是OB与另一条射线所成角的邻OB三分线．（直接写出答案）
【答案】(1)40°；
(2)30°或90°；
(3)1003秒或36秒或752秒或90秒或105秒
【分析】（1）根据三角形外角的性质可得∠A=∠ACD−∠ABC=60°，然后根据三分线的定义结合三角形外角的性质求解即可；
（2）由题意可知，共有三种情况：①当OA⊥ON时，即∠AON＝90°，②当OM⊥OB时，即∠MOB＝90°，③当OM⊥ON时，即∠MON=90°，分别根据角的和差及三分线的定义计算即可；
（3）由（2）可知，当∠AOC<∠BOC时，∠AOC＝30°，∠BON＝30°，可求得∠BOM＝110°，设运动时间为t秒，根据ON和OM转动后的位置，结合三分线的定义分情况求解即可．
【详解】（1）解：∵∠A=60°，∠ACD是△ABC的一个外角，
∴∠A=∠ACD−∠ABC=60°，
∵BF、CF是∠ABC和外角∠ACD的三分线，
∴∠FBC=23∠ABC，∠FCD=23∠ACD，
∴∠F=∠FCD−∠FBC=23∠ACD−23∠ABC=23∠ACD−∠ABC=23×60°=40°；
（2）解：由题意可知，共有两种情况：
①当OA⊥ON时，即∠AON＝90°，
∵∠AOB=120°，
∴∠BON＝∠AOB−∠AON=120°−90°=30°，
∵ON是∠BOC的邻OB三分线，
∴∠BOC＝3∠BON＝90°，
∴∠AOC＝120°－90°＝30°；
②当OM⊥OB时，即∠MOB＝90°，
∵∠AOB=120°，
∴∠AOM＝∠AOB−∠MOB=120°−90°=30°，
∵OM是∠AOC的邻OA三分线，
∴∠AOC＝3∠AOM＝90°，
当OM⊥ON时，即∠MON=90°，
∵∠AOB=120°，
∴∠AOM+∠BON=120°-90°=30°，
∵OM是∠AOC 的邻OA三分线，ON是∠BOC 的邻OB三分线，
∴∠AOC=3∠AOM，∠BOC=3∠BON，
∴∠AOB=∠AOC+∠BOC=3∠AOM+3∠BON=90°，
这与∠AOB=120°矛盾，∴OM⊥ON不成立，
综上，∠AOC的度数为30°或90°；
（3）解：由（2）可知，当∠AOC<∠BOC时，∠AOC＝30°，∠BON＝30°，
∵OM是∠AOC的邻OA三分线，
∴∠AOM＝13∠AOC＝10°，
∴∠BOM＝120°－10°＝110°，
设运动时间为t秒，分情况讨论：
当ON到达OB前，ON是∠BOM的邻OB三分线时，
由题意得：∠BOM＝3∠BON，即110−3t=330−t，
此方程无解，故此情况不存在；
当ON到达OB前，OM是∠BON的邻OB三分线时，
由题意得：3∠BOM＝∠BON，即3110−3t=30−t，
解得：t=752，
当t=752时，ON已经到达OB，与题意不符，故此情况不存在；
当ON到达OB返回至OC，OM到达OB前，ON是∠BOM的邻OB三分线时，
由题意得：∠BOM＝3∠BON，即110−3t=3t−30，
解得：t=1003；
当ON到达OB返回至OC，OM到达OB前，OM是∠BON的邻OB三分线时，
由题意得：3∠BOM＝∠BON，即3110−3t=t−30，
解得：t=36；
当ON到达OB返回至OC，OM到达OB返回至OC前，ON是∠BOM的邻OB三分线时，
由题意得：∠BOM＝3∠BON，即3t−110=3t−30，
此方程无解，故此情况不存在；
当ON到达OB返回至OC，OM到达OB返回至OC前，OM是∠BON的邻OB三分线时，
由题意得：3∠BOM＝∠BON，即33t−110=t−30，
解得：t=752；
当ON到达OB返回至OC，OM到达OB返回至OC再转向OB前，ON是∠BOM的邻OB三分线时，
由题意得：∠BOM＝3∠BON，即90−3t−110−90=3t−30，
解得：t=1903，
当t=1903时，OM尚未到达OC，与题意不符，故此情况不存在；
当ON到达OB返回至OC，OM到达OB返回OC再转向OB前，OM是∠BON的邻OB三分线时，
由题意得：3∠BOM＝∠BON，即390−3t−110−90=t−30，
解得：t=90；
当ON到达OB返回至OC，OM第二次转向OC时，此时只可能是OM是∠BON的邻OB三分线，
由题意得：3∠BOM＝∠BON，即33t−110−90−90=t−30，
解得：t=105，
综上，当转动1003秒或36秒或752秒或90秒或105秒后，OM，ON中，有一条射线是OB与另一条射线所成角的邻OB三分线．
【点睛】本题考查了角的和差计算，三角形外角的性质，一元一次方程的应用，正确理解三分线的定义，分情况讨论是解答本题的关键．
8．（2022春·江苏盐城·七年级统考期末）【教材呈现】苏科版义务教育数学教科书七下第42页第20题，是一道研究双内角平分线的夹角和双外角平分线夹角的数学问题，原题如下．
在△ABC中，∠A=n°．
（1）设∠B、∠C的平分线交于点O，求∠BOC的度数；
（2）设△ABC的外角∠CBD、∠BCE的平分线交于点O′，求∠BO′C的度数；
（3）∠BOC与∠BO′C有怎样的数量关系？
【问题解决】聪聪对上面的问题进行了研究，得出以下答案：
如图1，在△ABC中，∠A=n°．
(1) ∠ABC、∠ACB的平分线交于点O，则∠BOC的度数为________；
(2)△ABC的外角∠CBD、∠BCE的平分线交于点O′，则∠BO′C的度数为________；
(3)∠BOC与∠BO′C的数量关系是_________．
(4)【问题深入】
如图2，在△ABC中，∠ABC、∠ACB的角平分线交于点O，将△ABC沿MN折叠使得点A与点O重合，请直接写出∠1+∠2与∠BOC的一个等量关系式：
(5)如图3，过△ABC的外角∠CBD、∠BCE的平分线的交点O′，作直线PQ交AD于点P，交AE于点Q．当∠APQ=∠AQP时，∠CO′Q与∠ABC有怎样的数量关系？请直接写出结果．
【答案】(1)90°+12n°；
(2)90°−12n°；
(3)∠BOC+∠BO′C=180°；
(4)∠1+∠2=4∠BOC−360°；
(5)∠CO'Q=90°−12∠ABC
【分析】（1）由三角形内角和定理得到，∠ABC+∠ACB=180°−n°，再根据角平分线的定义，推出∠OBC+∠OCB=90°−12n°，即可求出∠BOC的度数；
（2）根据三角形外角的定义，推出∠CBD+∠BCE=180°+n°，再根据角平分线的定义，推出∠CBO′+∠BCO′=90°+12n°，然后利用三角形内角和定理即可求出∠BO′C的度数；
（3）根据（1）和（2）的结果即可得到答案；
（4）由折叠的性质可知，∠AMN=∠OMN，∠ANM=∠ONM，得到∠1=180°−2∠AMN，∠2=180°−2∠ONM，再根据三角形内角和定理，推出∠1+∠2=2∠A，由（1）同理可证∠BOC=90°+12∠A，据此即可得到答案；
（5）根据多边形内角和与角平分线的定义，推出∠BO′C=∠BPQ，再根据三角形外角的性质，得到∠CO′Q=∠PBO′，最后根据∠ABC=180°−2∠PBO′，即可得到答案．
【详解】（1）解：∵∠A=n°，
∴∠ABC+∠ACB=180°−n°，
∵BO平分∠ABC，CO平分∠ACB，
∴∠OBC=12∠ABC，∠OCB=12∠ACB，
∴∠OBC+∠OCB=12∠ABC+∠ACB=90°−12n°，
∴∠BOC=180°−∠OBC+∠OCB=180°−90°−12n°=90°+12n°，
故答案为：90°+12n°；
（2）解：∵∠CBD=∠A+∠ACB，∠BCE=∠A+∠ABC，
∴∠CBD+∠BCE=∠A+∠ACB+∠ABC+∠A=180°+∠A=180°+n°，
∵BO′平分∠CBD，CO′平分∠BCE，
∴∠CBO′=12∠CBD，∠BCO′=12∠BCE，
∴∠CBO′+∠BCO′=12∠CBD+∠BCE=90°+12n°，
∴∠BO′C=180°−∠CBO′+∠BCO′=180°−90°+12n°=90°−12n°，
故答案为：90°−12n°；
（3）解：由（1）和（2）可知，∠BOC=90°+12n°，∠BO′C=90°−12n°，
∴∠BOC+∠BO′C=180°，
故答案为：∠BOC+∠BO′C=180°
（4）解：∠1+∠2=4∠BOC−360°，理由如下：
由折叠的性质可知，∠AMN=∠OMN，∠ANM=∠ONM，
∴∠1=180°−∠AMN−∠OMN=180°−2∠AMN，∠2=180°−∠ANM−∠ONM=180°−2∠ONM，
∵∠AMN+∠ANM=180°−∠A，
∴∠1+∠2=180°−2∠AMN+180°−2∠ANM=360°−2∠AMN+∠ANM=2∠A，
由（1）同理可证，∠BOC=90°+12∠A，
∴2∠A=4∠BOC−360°，
∴∠1+∠2=4∠BOC−360°；
（5）解：∵四边形BCQP的内角和为360°，
∴∠CBP+∠BPQ+∠PQC+∠BCQ=360°，
∵BO′平分∠CBD，CO′平分∠BCE，
∴∠CBD=2∠CBO′，∠BCE=2∠BCO′，
∵∠APQ=∠AQP，
∴2∠CBO′+2∠BPQ+2∠BCO′=360°，
∴∠CBO′+∠BPQ+∠BCO′=180°，
∴∠CBO′+∠BCO′+∠BO′C=180°，
∴∠BO′C=∠BPQ，
∵∠BO′Q=∠BPQ+∠PBO′=∠BO′C+∠CO′Q，
∴∠CO′Q=∠PBO′，
∵∠ABC=180°−∠CBD=180°−2∠PBO′，
∴∠ABC=180°−2∠CO′Q，
∴∠CO'Q=90°−12∠ABC．
【点睛】本题考查了角平分线的定义，三角形外角的性质，三角形内角和定理，多边形内角和，根据图形找出角度之间的数量关系是解题关键．
9．（2022春·江苏苏州·七年级苏州高新区实验初级中学校考期末）已如在四边形ABCD中，∠A=∠C=90°．
（1）如图1，若∠ABC=70°，则∠NDC=________．
（2）如图2，若BF、DE分别平分∠CBM、∠CDN，判断DE与BF位置关系并证明理由．
（3）如图3，若BP、DP分别五等分∠CBM、∠CDN（即∠CBP=15∠CBM，∠CDP=15∠CDN），则∠P=_______．
【答案】（1）70°；（2）DE∥BF，证明见解析；（3）54°
【分析】（1）根据四边形内角和计算即可；
（2）根据平角的定义和等量代换可得∠MBC+∠CDN=180°，再根据角平分线的定义得到∠CBF+∠CDE=90°，从而推出∠EDB+∠FBD=180°，可得结论；
（3）根据五等分得到∠CDP+∠CBP=36°，连接PC并延长，证明∠DCB=∠DPB+∠CBP+∠CDP，即可计算．
【详解】解：（1）∵∠A=∠C=90°，∠ABC=70°，
∴∠ADC=360°-90°-90°-70°=110°，
∴∠NDC=180°-110°=70°；
（2）DE∥BF，如图，连接BD，
∵∠ABC+∠ADC=180°，
且∠MBC+∠ABC=180°，∠CDN+∠ADC=180°，
∴∠MBC+∠CDN=180°，
∵∠CBF=12∠MBC，∠CDE=12∠CDN，
∴∠CBF+∠CDE=90°，
∵∠C=90°，
∴∠CBD+∠CDB=90°，
∴∠EDB+∠FBD=∠CBF+∠CDE+∠CBD+∠CDB=180°，
∴DE∥BF；
（3）∵∠MBC+∠CDN=180°，
∴∠CDP+∠CBP=15（∠MBC+∠CDN）=36°，
连接PC并延长，
∵∠DCE=∠CDP+∠CPD，∠BCE=∠CPB+∠CBP，
∴∠DCB=∠DCE+∠BCE=∠DPB+∠CBP+∠CDP，
∴∠DPB=90°-36°=54°．
【点睛】本题考查多边形内角和与外角，三角形内角和定理，平行线的判定等知识，解题的关键是学会添加常用辅助线，属于中考常考题型．
10．（2022春·江苏盐城·七年级统考期末）在一个各内角都相等的多边形中，每一个内角都比相邻外角的3倍还大20°．
（1）求这个多边形的边数；
（2）若将这个多边形剪去一个角，剩下多边形的内角和是多少？
【答案】（1）9；（2）1080º或1260º或1440º．
【分析】（1）设多边形的一个外角为x，则与其相邻的内角等于3x+20°，根据内角与其相邻的外角的和是 180°列出方程，求出x的值，再由多边形的外角和为360°，求出此多边形的边数为360°x；
（2）剪掉一个角以后，多边形的边数可能增加了1条，也可能减少了1条，或者不变，根据多边形的内角和定理即可求出答案．
【详解】解：（1）设每一个外角为x，则与其相邻的内角等于3x+20°，
∴180°−x=3x+20°，
∴x=40°，即多边形的每个外角为40°，
∵多边形的外角和为360°，
∴多边形的外角个数为：360°40°=9，
∴这个多边形的边数为9；
（2）因为剪掉一个角以后，多边形的边数可能增加了1条，也可能减少了1条，或者不变，
①若剪去一角后边数减少1条，即变成8边形，
∴内角和为8−2×180°=1080°，
②若剪去一角后边数不变，即变成9边形，
∴内角和为9−2×180°=1260°，
③若剪去一角后边数增加1，即变成10边形，
∴内角和为10−2×180°=1440°，
∴将这个多边形剪去一个角后，剩下多边形的内角和为1080°或1260°或 1440°．
【点睛】本题考查了多边形的内角和定理，外角和定理，多边形内角与外角的关系，熟练掌握相关知识点是解题的关键．
考点2
幂的运算解答期末真题压轴题
1．（2022春·江苏·七年级期末）阅读材料：31的末尾数字是3，32的末尾数字是9，33的末尾数字是7，34的末尾数字是1，35的末尾数字是3，，观察规律，34n+1=(34)n×3，∵34的末尾数字是1，∴(34)n的末尾数字是1，∴(34)n×3的末尾数字是3，同理可知，34n+2的末尾数字是9，34n+3的末尾数字是7．解答下列问题：
(1)32021的末尾数字是 ，142022的末尾数字是 ；
(2)求22022的末尾数字；
(3)求证：122024+372018能被5整除．
【答案】(1)3，6；
(2)4；
(3)证明见解析．
【分析】（1）根据阅读材料中的结论可知32021的末尾数字；根据阅读材料中提供的方法，可得142n+1的末尾数字是4，142n的末尾数字是6，于是得解；
（2）先将22022化成(24)505×4，再利用(24)505=16505的末尾数字是6，从而得出结论；
（3）分别证明122024的末尾数字为6和372018的末尾数字9，则命题即可得证．
【详解】（1）解：∵ 32021=34×505+1，
∴32021的末尾数字为3；
∵141的末尾数字是4，142的末尾数字是6，143的末尾数字是4，…
∴142n+1的末尾数字是4，142n的末尾数字是6，
∴ 142022的末尾数字是6；
故答案为：3，6；
（2）解：22022=(24)505×22=(24)505×4，
∵(24)505的末尾数字是6，
∴22022的末尾数字是4；
（3）证明：∵121的末尾数字是2，122的末尾数字是4，123的末尾数字是8，124的末尾数字是6，125的末尾数字是2，…
∴ 124n+1的末尾数字是2，124n+2的末尾数字是4，124n+3的末尾数字是8，124n的末尾数字是6，
∴122024=124×506的末尾数字为6；
同理可得：
374n+1的末尾数字7，374n+2的末尾数字9，374n+3的末尾数字3，374n的末尾数字1；
∴ 372018=374×504+2的末尾数字9，
∴122024+372018的末尾数字是5，
∴122024+372018能被5整除．
【点睛】此题是一道阅读理解题，主要考查了幂的运算、数的整除，熟练掌握同底数幂的乘法、幂的乘方与积的乘方法则是解答此题的关键．
2．（2022春·江苏·七年级期末）如果10b=n，那么b为n的“劳格数”，记为b=d（n）．由定义可知：10b=n与b=d（n）表示b、n两个量之间的同一关系．
(1)根据“劳格数”的定义，填空：d（10）=____ ，d（10-2）=______；
(2)“劳格数”有如下运算性质：
若m、n为正数，则d（mn）=d（m）+d（n），d（mn）=d（m）-d（n）；根据运算性质，填空：d(a3)d(a)=________．（a为正数）
(3)若d（2）=0.3010，分别计算d（4）；d（5）．
【答案】(1)1，﹣2
(2)3
(3)0.6020，0.699．
【分析】（1）由“劳格数”的定义运算转化为同底数幂解答即可；
（2）根据幂的乘方公式转化求解即可；
（3）根据积的乘方公式、幂的乘方转化求解即可.
【详解】（1）解：∵10b＝10，
∴b＝1，
∴d（10）＝1；
10b＝10﹣2，∴b＝﹣2，
∴d（10﹣2）＝﹣2；
故答案为1，﹣2；
（2）解：∵d（mn）=d（m）+d（n），d（mn）=d（m）-d（n）
∴d(a3)d(a)=3d(a)d(a)=3
故答案为3；
（3）解：∵d（2）＝0.3010，
∴d（4）＝2d（2）＝0.6020，
d（5）＝d（102）＝d（10）﹣d（2）＝1﹣0.3010＝0.699．
【点睛】本题考查新定义，有理数的运算；理解题意，将新定义转化为同底数幂的乘除法、幂的乘方与积的乘方运算是解题的关键.
3．（2022春·江苏·七年级期末）阅读下列材料：小明为了计算1+2+22+⋅⋅⋅+22020+22021的值，采用以下方法：
设S=1+2+22+⋅⋅⋅+22020+22021①
则2S=2+22+⋅⋅⋅+22021+22022②
②−①得，2S−S=S=22022−1．
请仿照小明的方法解决以下问题：
（1）2+22+⋅⋅⋅+220=______；
（2）求1+12+122+⋅⋅⋅++1250=______；
（3）求−2+−22+⋅⋅⋅+−2100的和；（请写出计算过程）
（4）求a+2a2+3a3+⋅⋅⋅+nan的和（其中a≠0且a≠1）．（请写出计算过程）
【答案】（1）221−2；（2）2-1250；（3）2101−23；（4）a−an+1a−12+nan+1a−1
【分析】（1）根据阅读材料可得：设s＝2+22+⋅⋅⋅+220①，则2s＝22＋23＋…＋220＋221②，②−①即可得结果；
（2）设s＝1+12+122+⋅⋅⋅+1250①，12s＝12+122+⋅⋅⋅+1250+1251②，②−①即可得结果；
（3）设s＝−2+−22+⋅⋅⋅+−2100①，-2s＝−22+−23+⋅⋅⋅+−2101②，②−①即可得结果；
（4）设s＝a+2a2+3a3+⋅⋅⋅+nan①，as＝a2+2a3+3a4+⋅⋅⋅+nan+1②，②−①得as-s=-a-a2−a3−a4+⋅⋅⋅−an+nan+1，同理：求得-a2−a3−a4+⋅⋅⋅−an+1，进而即可求解．
【详解】解：根据阅读材料可知：
（1）设s＝2+22+⋅⋅⋅+220①，
2s＝22＋23＋…＋220＋221②，
②−①得，2s−s＝s＝221−2；
故答案为：221−2；
（2）设s＝1+12+122+⋅⋅⋅+1250①，
12s＝12+122+⋅⋅⋅+1250+1251②，
②−①得，12s−s＝-12s＝1251-1，
∴s＝2-1250，
故答案为：2-1250；
（3）设s＝−2+−22+⋅⋅⋅+−2100①
-2s＝−22+−23+⋅⋅⋅+−2101②
②−①得，-2s−s＝-3s＝−2101+2
∴s＝2101−23；
（4）设s＝a+2a2+3a3+⋅⋅⋅+nan①，
as＝a2+2a3+3a4+⋅⋅⋅+nan+1②，
②-①得：as-s=-a-a2−a3−a4+⋅⋅⋅−an+nan+1，
设m=-a-a2−a3−a4+⋅⋅⋅−an③，
am=-a2−a3−a4+⋅⋅⋅−an+1④，
④-③得：am-m=a-an+1，
∴m=a−an+1a−1，
∴as-s=a−an+1a−1+nan+1，
∴s=a−an+1a−12+nan+1a−1．
【点睛】本题考查了规律型−实数的运算，解决本题的关键是理解阅读材料进行计算．
4．（2022秋·江苏扬州·七年级扬州市竹西中学校考期末）(1)你发现了吗？(23)2=23×23，(23)−2=1(23)2=123×123=32×32，由上述计算，我们发现(23)2___(32)−2；
(2)请你通过计算，判断(54)3与(45)−3之间的关系；
(3)我们可以发现：(ba)−m____(ab)m (ab≠0)
(4)利用以上的发现计算：(715)−3×(75)4.
【答案】（1）=；（2）=；（3）=；（4）1895.
【分析】（1）类比题干中乘方的运算即可得；
（2）类比题干中分数的乘方计算方法计算后即可得；
（3）根据（1）、（2）的规律即可得；
（4）逆用积的乘方将原式变形为(715)-3×(75)4=(157)3×(75)4，再利用同底数幂进行计算可得．
【详解】（1）我们发现(23)2 = (32)−2
（2）计算得(54)3=12564， (45)-3=12564
∴(54)3=(45)-3
（3）我们可以发现：(ba)−m = (ab)m（ab≠0）.
（4）利用以上的发现计算：(715)-3×(75)4=(157)3×(75)4= (157)3×(75)3×(75)=1895
5．（2022春·江苏泰州·七年级校考期末）利用图形来表示数量或数量关系，也可以利用数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合．你能利用数形结合的思想解决下列问题吗?
(1)如图①，一个边长为1的正方形，依次取正方形面积的12，14，18，…，12n，根据图示我们可以知道：12+14+18+116+⋯+164=_____________；那么12+14+18+116+⋯+12n=____________；
(2)如图②，一个边长为1的正方形，依次取剩余部分的23，根据图示：计算：23+29+227+⋯+23n=___________；
(3)如图③是一个边长为1的正方形，根据图示：计算：13+29+427+881+⋯+2n−13n=_________．（用含n的式子表示）
【答案】(1)6364，1−12n
(2)1−13n
(3)1−2n3n
【分析】（1）根据题意找出规律进行计算即可；
（2）根据题干给出图形，依次取正方形面积的23,29,227，…，找出规律即可；
（3）根据题干给出图形，依次取正方形面积的13,29,427，…，找出规律即可．
【详解】（1）解：∵第1次截取后剩余12，
第2次截取后剩余12×12=122，
第3次截取后剩余12×12×12=123，
…，
第n次截取后剩余12×12×...×12n个=12n，
∴12+14+18+116+⋯+164=1−126=6364，12+14+18+116+12n=1−12n．
故答案为：6364，1−12n．
（2）解：∵第1次截取后剩余13，
第2次截取后剩余13×13=132，
第3次截取后剩余13×13×13=133，
…，
第n次截取后剩余13×13×...×13n个=13n，
∴23+29+227+23n=1−13n．
故答案为：1−13n．
（3）解：∵第1次截取后剩余23，
第2次截取后剩余23×23=2232，
第3次截取后剩余23×23×23=2333，
…，
第n次截取后剩余23×23×...×23n个=2n3n，
∴13+29+427+881+2n−13n=1−2n3n．
故答案为：1−2n3n．
【点睛】本题考查的图形的变化类，根据题干给出的图形，利用数形结合求解是解答此题的关键．
6．（2022春·江苏盐城·七年级统考期末）乐于思考的小宏在学习《幂的运算》时发现：若am=an（a>0，且a≠1，m、n都是正整数），则m=n，例如：若5m=54，则m=4，小宏将这个发现与老师分享，并得到老师确认是正确的，请用小宏发现的这个正确结论解决下面的问题：
(1)如果2×4x×32x=812，求x的值；
(2)如果5x+2+5x+1=750，求x的值.
【答案】(1)x=5；
(2)x=2
【分析】（1）利用幂的乘方的法则及同底数幂的乘法的法则对式子进行整理，从而可求解；
（2）利用同底数幂的乘法的法则及幂的乘方的法则对式子进行整理，即可求解．
【详解】（1）解：∵2×4x×32x=812，
∴2×22x×25x=236，
即21+7x=236，
∴1+7x=36，
解得：x=5；
（2）∵5x+2+5x+1=750，
∴5×5x+1+5x+1=6×125，6×5x+1=6×53，
即5x+1=53，
∴x+1=3，
解得：x=2．
【点睛】本题考查幂的乘方，同底数幂的乘法，解答的关键是对相应的运算法则的掌握与运用．
7．（2022春·江苏扬州·七年级校联考期末）求值：
(1)已知2x+5y+3=0，求4x⋅32y的值；
(2)已知3x+1−3x=54，求x的值．
【答案】(1)18
(2)x=3
【分析】（1）先求出2x+5y=−3，再根据4x⋅32y=22x+5y进行求解即可；
（2）由3x+1−3x=54可得3⋅3x−3x=54，进而得到3x=27=33，则x=3．
【详解】（1）解：∵2x+5y+3=0，
∴2x+5y=−3，
∴4x⋅32y
=22x⋅25y
=22x⋅25y
=22x+5y
=2−3
=18；
（2）解：∵3x+1−3x=54，
∴3⋅3x−3x=54，
∴2⋅3x=54，
∴3x=27，
∴x=3．
【点睛】本题主要考查了同底数幂乘法和同底数幂乘法的逆运算，幂的乘方和幂的乘方的逆运算，负整数指数幂，熟知相关计算法则是解题的关键．
8．（2022春·江苏·七年级统考期末）规定两数a，b之间的一种运算，记作(a，b)；如果ac=b，那么(?，?)=?． 例如：因为23=8，所以2，8=3
(1)根据上述规定，填空：
(3，9)=___________，(___________，16)=2，(−2，−8)=___________；
(2)有同学在研究这种运算时发现一个现象；(3n,4n)=(3,4),，他给出了如下的证明：
设(3n,4n)=x,
∴(3n)x=4n
即(3x)n=4n
∵3x>0
∴3x=4
即(3,4)=x,
∴(3n,4n)=(3,4)
①若(4,5)=a,(4,6)=b,(4,30)=c，请你尝试运用上述这种方法证明a+b=c．
②猜想(x−1)n,(y+1)n+(x−1)n,(y−2)n=(___________，___________)(结果化成最简形式)
【答案】(1)2；±4；3
(2)①见解析；②(x−1)，(y2−y−2)
【分析】（1）根据规定的两数之间的运算法则解答；
（2）①根据同底数幂的乘法法则，结合定义证明；
②根据例题和①中证明的式子作为公式进行变形即可．
【详解】（1）解：∵32=9，∴(3，9)=2；
∵(±4)2=16，∴(±4，16)=2
∵−23=−8，∴(−2，−8)=3,
故答案为：2；±4；3．
（2）①证明
∵(4,5)=a,(4,6)=b,(4,30)=c
∴4a=5,4b=6,4c=30
∴4a×4b=30=4c
即4a+b=4c
∴a+b=c．
②∵(3n,4n)=(3,4)
∴(x−1)n,(y+1)n+(x−1)n,(y−2)n
=x−1,y+1+x−1,y−2
=x−1,y+1y−2
=(x−1),(y2−y−2)；
故答案为：(x−1),(y2−y−2)．
【点睛】本题考查的是新定义的理解和掌握，还考查了同底数幂的乘法以及整式的混合运算，弄清题中的新运算是解本题的关键．
9．（2022春·江苏·七年级期末）阅读：已知正整数a、b、c，显然，当同底数时，指数大的幂也大，若对于同指数，不同底数的两个幂ab和cb，当a>c时，则有ab>cb，根据上述材料，回答下列问题．
(1)比较大小：520 420（填写＞、＜或＝）．
(2)比较233与322的大小（写出具体过程）．
(3)已知2a=3，8b=6，求28+2b3的值．
【答案】(1)>
(2)233<322
(3)603979776
【分析】（1）根据同指数，不同底数的两个幂ab和cb，当a>c时，则有ab>cb，即可进行解答；
（2）将根据幂的乘方的逆运算，将233与322转化为同指数的幂，再比较大小即可；
（3）根据同底数幂乘法的逆运算，将28+2b3转化为28×22b3，再根据积的乘方的逆运算，整理为含有28和8b的形式，进行计算即可．
【详解】（1）解：∵5>4，
∴520>420，
故答案为：>．
（2）∵233=2311=811，
322=3211=911，
∵8<9，
∴233<322．
（3）∵8b=6，
∴23b=6，
∴28+2b3
=28•22b3
=224•26b
=224•23b2
=224×62
=603979776．
【点睛】本题主要考查了幂的乘方与积的乘方的运算法则和逆运算，解题的关键是熟练掌握幂的乘方和积的乘方的运算法则及其逆运算法则．
10．（2022春·江苏·七年级期末）阅读以下材料：
指数与对数之间有密切的联系，它们之间可以互化．
对数的定义：一般地，若ax=N (a>0且a≠1)，那么x叫做以a为底N的对数，记作x=lgaN，比如指数式24=16可以转化为对数式4=lg216，对数式2=lg525，可以转化为指数式52=25．
我们根据对数的定义可得到对数的一个性质：
lga(M⋅N)=lgaM+lgaN (a>0，a≠1，M>0，N>0)，理由如下：
设lgaM=m，lgaN=n，则M=am，N=an，
∴M⋅N=am⋅an=am+n，由对数的定义得m+n=lga(M⋅N)
又∵m+n=lgaM+lgaN，
∴lga(M⋅N)=lgaM+lgaN．
请解决以下问题：
(1)将指数式34=81转化为对数式_______；
(2)求证：lga MN= lgaM−lgaN(a>0，a≠1，M>0，N>0)；
(3)拓展运用：计算lg69+lg68−lg62=______．
【答案】(1)4=lg381
(2)证明见解析
(3)2
【分析】（1）根据指数与对数的关系求解．
（2）根据指数与对数的关系求证．
（3）利用（1）、（2）中的对数运算法则求解．
【详解】（1）解：根据指数与对数关系得：4=lg381．
故答案为：4=lg381．
（2）解：设lgaM=m，lgaN= n，则M=am，N=an，
∴MN= am÷an=am−n．
∴lga MN= lgaam−n=m−n=lgaM−lgaN．
∴lga MN= lgaM−lgaN．
（3）解：原式=lg69×8÷2
=lg636
=2．
故答案为：2．
【点睛】本题考查了新定义的知识解题，理解新定义，找到指数和对数的关系是求解本题的关键．
考点3
整式乘法与因式分解解答期末真题压轴题
1．（2022春·江苏·七年级期末）【阅读材料】配方法是数学中重要的一种思想方法．它是指将一个式子的某一部分通过恒等变形化为完全平方式或几个完全平方式的和的方法．这种方法常被用到代数式的变形中，并结合非负数的意义来解决一些问题．
我们定义：一个整数能表示成a2+b2（a、b是整数）的形式，则称这个数为“完美数”．例如，5是“完美数”．理由：因为5=22+12，所以5是“完美数”．
【解决问题】
（1）数53______“完美数”（填“是”或“不是”）；
【探究问题】
（2）已知x2+y2−4x+2y+5=0，则x+y=______；
（3）已知S=2x2+y2+2xy+12x+k（x、y是整数，k是常数），要使S为“完美数”，试求出符合条件的k值，并说明理由．
【拓展结论】
（4）已知实数x、y满足−x2+72x+y−3=0，求x−2y的最大值．
【答案】（1）是；（2）1；（3）k=36，理由见解析；（4）x−2y的最大值为2．
【分析】（1）把59分为两个整数的平方即可；
（2）已知等式利用完全平方公式配方后，根据非负数的性质求出x与y的值，即可求出x+y的值；
（3）根据S为“完美数”，利用完全平方公式配方，确定出k的值即可；
（4）由已知等式表示出y，代入x−2y中，配方后再利用非负数的性质求出最大值即可．
【详解】解：（1）根据题意得：53=22+72．
故答案为：是；
（2）已知等式变形得：x2−4x+4+y2+2y+1=0，
即x−22+y+12=0，
∵x−22≥0，y+12≥0，
∴x−2=0，y+1=0，
解得：x=2，y=−1，
则：x+y=2−1=1．
故答案为：1；
（3）当k=36时，S为“完美数”，理由如下：
S=2x2+y2+2xy+12x+k
=x2+12x+k+y2+2xy+x2
=x2+12x+k+y+x2，
∵S是完美数，
∴x2+12x+k是完全平方式，
∴k=36；
（4）∵−x2+72x+y−3=0，
∴−y=−x2+72x−3，即−2y=−2x2+7x−6，
∴x−2y=x−2x2+7x−6
=−2x2+8x−6
=−2x2−4x+4+2
=−2x−22+2，
当x=2时，x−2y最大，最大值为2．
【点睛】本题考查了配方法的应用，熟练掌握完全平方公式是解本题的关键．
2．（2022春·江苏镇江·七年级统考期末）如图1是一个长为4a、宽为b的长方形，沿图1中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形（如图2）．
(1)观察图2，请你写出a+b2、a−b2、ab之间的等量关系是________；
(2)利用（1）中的结论，若x+y=5，xy=94，求x−y2的值；
(3)如图3，点C是线段AB上的一点，分别以AC、BC为边在AB的同侧作正方形ACDE和正方形CBFG，连接EG、BG、BE，当BC=1时，△BEG的面积记为S1，当BC=2时，△BEG的面积记为S2,⋯，以此类推，当BC=n时，△BEG的面积记为Sn，计算S50−S49+S48−S47+⋯+S2−S1的值．
【答案】(1)4ab=a+b2−a−b2
(2)16
(3)12752
【分析】（1）通过观察图形可以发现，大正方形是由四个矩形与中间的小正方形组成，据此进一步分析求解即可；
（2）根据（1）中的结论进一步代入计算即可；
（3）连接EC，证明出EC∥BG，再利用△BEG的面积与△BGC的面积相等得出Sn=n22，从而得到Sn−Sn−1=n−12据此进一步计算即可．
【详解】（1）由图1和图2中矩形的面积为等量得：
4ab=a+b2−a−b2
故答案为：4ab=a+b2−a−b2；
（2）由（1）中公式可得：
a−b2=a+b2−4ab．
同理可得：
x−y2=x+y2−4xy
=52−4×94
=16；
（3）连接EC，
在正方形ACDE和正方形BCGF中，∠ECD=∠CGB=45°，
∴EC∥BG，
∴△BGE和△BGC的边BG上的高相等，
∴S△BGE=S△BGC．
当BC=1时，S1=12×1×1=122，
当BC=2时，S2=12×2×2=222，
……
当BC=n时，Sn=n22，
∴Sn−Sn−1=n+n−1n−n+12=n+n−12
∴S50−S49+S48−S47+...+S2−S1
=S50−S49+S48−S47+...+S2−S1
=50+492+48+472+...+2+12
=50+49+48+47+...+2+12
=1+50×252
=12752．
【点睛】本题主要考查了完全平方公式的几何背景，观察图形，找出相应的规律是解题关键．
3．（2022春·江苏南京·七年级统考期末）知识生成：我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式．例如图1可以得到(a+b)2=a2+2ab+b2，基于此，请解答下列问题：
(1)直接应用：若xy=7,x+y=5，直接写出x2+y2的值______；
(2)类比应用：填空：①若x3−x=4，则x2+(x−3)2=______；
②若x−2019x−2023=2，则(x−2019)2+(x−2023)2=_______；
(3)知识迁移，两块完全相同的特制直角三角板（∠AOB=∠COD=90°）如图2所示放置，其中A，O，D在一直线上，连接AC，BD，若AD=16,S△AOC+S△BOD=60，求一块三角板的面积．
【答案】(1)11
(2)1，20
(3)一块直角三角板的面积为34．
【分析】（1）根据完全平方公式的变形可得答案；
（2）①设x=m，3−x=n，则mn=4，m+n=3，由x2+(x−3)2=m2+n2=(m+n)2−2mn进行计算即可；
②设x−2019=a，x−2023=b，则ab=(x−2019)(x−2023)=2，a−b=4，由(x−2019)2+(x−2023)2=a2+b2=(a−b)2+2ab进行计算即可；
（3）设AO=p，DO=q，由题意可得，p+q=16，p2+q2=120，由2pq=(p+q)2−(p2+q2)求出12pq的值即可．
【详解】（1）解：∵xy=7,x+y=5，
∴x2+y2=(x+y)2−2xy=52−2×7=11，
故答案为：11；
（2）解：①设x=m，3−x=n，则mn=4，m+n=3，
∴x2+(x−3)2=m2+n2
=(m+n)2−2mn
=9−8
=1，
故答案为：1；
②设x−2019=a，x−2023=b，则ab=2，a−b=4，
∴(x−2019)2+(x−2023)2=a2+b2=(a−b)2+2ab
=42+4
=20，
故答案为：20；
（3）解：设AO=p，DO=q，
∵AD=16，S△AOC+S△BOD=60，
∴p+q=16，12p2+12q2=60，
即p+q=16，p2+q2=120，
∴2pq=(p+q)2−(p2+q2)
=162−120，
即pq=68，
∴S直角三角板=12pq=34，
答：一块直角三角板的面积为34．
【点睛】本题考查完全平方公式的几何背景，多项式乘多项式，掌握完全平方公式的结构特征是正确解答的前提，掌握完全平方公式的变形是正确解答的关键．
4．（2022春·江苏苏州·七年级统考期末）阅读：在计算x−1xn+xn−1+xn−2+⋯+x+1的过程中，我们可以先从简单的、特殊的情形入手，再到复杂的、一般的问题，通过观察、归纳、总结，形成解决一类问题的一般方法，数学中把这样的过程叫做特殊到一般．如下所示：
【观察】①(x−1)(x+1)=x2−1；
②(x−1)x2+x+1=x3−1；
③(x−1)x3+x2+x+1=x4−1；
……
(1)【归纳】由此可得：x−1xn+xn−1+xn−2+⋯+x+1= ________；
(2)【应用】请运用上面的结论，解决下列问题：计算：22023+22022+22021+⋯+22+2+1=_______；
(3)计算：220−219+218−217+⋯−23+22−2+1=______；
(4)若x5+x4+x3+x2+x+1=0，求x2022的值．
【答案】(1)xn+1−1
(2)22024−1
(3)13×221−13
(4)x2022=1．
【分析】（1）利用已知得出式子变化规律，进而得出答案；
（2）利用（2）中变化规律进而得出答案；
（3）将220−219+218−217+⋯−23+22−2+1转化为−220+−219+−218+−217+⋯+−23+−22+−2+1，再利用（2）中变化规律进而得出答案；
（4）利用（2）中变化规律得出x的值，进而得出答案．
【详解】（1）解：①(x−1)(x+1)=x2−1；
②(x−1)x2+x+1=x3−1；
③(x−1)x3+x2+x+1=x4−1；
……；
∴x−1xn+xn−1+xn−2+⋯+x+1=xn+1−1，
故答案为：xn+1−1；
（2）解：22023+22022+22021+⋯+22+2+1
=2−122023+22022+22021+⋯+22+2+1
=22024−1；
（3）解：220−219+218−217+⋯−23+22−2+1
=−220+−219+−218+−217+⋯+−23+−22+−2+1
=−13×−2−1−220+−219+−218+−217+⋯+−23+−22+−2+1
=−13×−221−1
=13×221−13；
故答案为：13×221−13；
（4）解：∵x−1x5+x4+x3+x2+x+1=x5−1=0，
∴x=±1，
∵x5+x4+x3+x2+x+1=0，
∴x≠1，x=−1，
∴x2022=−12022=1．
【点睛】此题主要考查了平方差公式以及数字变化规律，正确得出式子之间的变化规律是解题关键．
5．（2022春·江苏苏州·七年级统考期末）填空：
a−ba+b=a2−b2；
a−ba2+ab+b2=a3−b3；
a−ba3+a2b+ab2+b3=a4−b4；
…
(1)a−ba2022+a2021b+⋯+ab2021+b2022=______；
(2)猜想：
a−ban−1+an−2b+⋯+abn−2+bn−1______；（其中n为正整数，且n≥2）
(3)利用（2）中的猜想的结论计算：
①1+2+22+⋯+22021+22022+22023
②310−39+38−37⋯+34−33+32−3．
【答案】(1)a2023−b2023
(2)an−bn
(3)①22024−1，②44286
【分析】（1）根据题中条件总结归纳即可求解；
（2）根据题中条件总结归纳即可求解；
（3）①根据题中条件可得a=2,b=1，即可求出答案；②由题意可得：a=3,b=−1，从而求得答案．
【详解】（1）解：根据上式总结归纳得：a−ba2022+a2021b+⋯+ab2021+b2022=a2023−b2023，
故答案为：a2023−b2023；
（2）解：根据上式猜想得：a−ban−1+an−2b+⋯+abn−2+bn−1=an−bn，
故答案为：an−bn；
（3）解：①1+2+22+⋯+22021+22022+22023
=22023+22022×1+22021×12++22×12021+2×12022+12023
∴a=2,b=1，
∴原式=22024−1；
②由题意可得：a=3,b=−1，
∴310−39+38−37⋯+34−33+32−3
=3−−1×310+39×−11+38×−12++33×−17+32×−18−31×−19+−110=311−−111=177148
∴310−39+38−37⋯+34−33+32−3=14×311+1−1=44286．
【点睛】本题考查了新定义下的运算，灵活运用题中条件是解题关键．
6．（2022春·江苏泰州·七年级校考期末）若x满足5−xx−2=2，
求x−52+2−x2的值．
解：设5−x=a，x−2=b，
则5−xx−2=ab=2，a+b=5−x+x−2=3，
所以x−52+2−x2=5−x2+x−22=a2+b2=a+b2−2ab=32−2×2=5．
请运用上面的方法求解下面的问题：
(1)若x满足若2023−xx−2021=−2022，则2023−x2+x−20212的值为_____．
(2)已知正方形ABCD的边长为x，E、F分别是AD、DC上的点，且AE=1，CF=3，长方形EMFD的面积是35，则长方形EMFD的周长为_____．
【答案】(1)4048；
(2)24．
【分析】（1）设2023−x=a，x−2021=b，则ab=−2022，a+b=2，依据a2+b2=a+b2−2ab即可求解；
（2）依题意得ED=x−1，DF=x−3，则x−1x−3=35，设x−1=a，x−3=b，则ab=35，a−b=2，依据a2+b2=a−b2+2ab求出a2+b2，再依据a+b2=a2+b2+2ab求出a+b2即a+b，即可求解．
【详解】（1）解：设2023−x=a，x−2021=b，
则2023−xx−2021=ab=−2022，2023−x+x−2021=a+b=2，
2023−x2+x−20212=a2+b2
=a+b2−2ab
=22−2×−2022
=4048，
故答案为：4048；
（2）依题意得：ED=x−1，DF=x−3，
则x−1x−3=35，
设x−1=a，x−3=b，
则x−1x−3=ab=35，x−1−x−3=a−b=2，
∴a2+b2=a−b2+2ab =22−2×35 =74，
∴a+b2=a2+b2+2ab =74+2×35 =144，
∴a+b=144=12，
∴ED+DF=a+b=12
则长方形EMFD的周长为：2a+b=24，
故答案为：24．
【点睛】本题考查了完全平方公式的综合应用；解题的关键是熟练掌握完全平方公式．
7．（2022春·江苏·七年级期末）【知识生成】
我们知道，图形是一种重要的数学语言，我国著名的数学家华罗庚先生曾经说：“数缺形时少直观，形缺数时难入微”．在学习整式的乘法时可以发现：用两种不同的方法表示同一个图形的面积，可以得到一个等式，进而可以利用得到的等式解决问题．
(1)根据图1，可以得到等式：a+b2=a2+2ab+b2，从而验证了完全平方公式．这体现的数学思想是______（填选项）：
A．分类讨论 B．转化 C．由特殊到一般 D．数形结合
(2)根据图2，可以得到等式：______；
(3)①图3是由几个小正方形和小长方形拼成的一个边长为a+b+c的大正方形，用不同的方法表示这个大正方形的面积，可以得到等式______；
②已知a+b+c=9，ab+bc+ac=26．利用①中所得到的等式，直接写出代数式a2+b2+c2的值为______；
(4)画出一个几何图形，使它的面积能表示2a+ba+2b=2a2+5ab+2b2．
【知识迁移】
(5)①类似地，利用立体图形体积的等量关系也可以得到某些数学公式．如图4，是用2个小正方体和6个小长方体拼成的一个棱长为a+b的大正方体．用不同的方法表示这个大正方体的体积，可以得到的等式为______；
②已知a+b=5，ab=6，利用①中所得的等式，直接写出代数式a3+b3的值为______．
(6)图5表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体，请你根据图中图形的变化关系，写出一个代数恒等式：______．
【答案】(1)D
(2)a−b2=a2−2ab+b2
(3)①a+b+c2=a2+b2+c2+2ab+2bc+2ac；②29
(4)见解析
(5)①a+b3=a3+3a2b+3ab2+b3；②35
(6)x3−x=xx−1x+1
【分析】（1）体现的数学思想是数形结合；
（2）根据图形的面积的两种不同计算方法得到完全平方公式；
（3）①先用正方形的面积公式表示出面积，再用几个小正方形和小长方形的面积的和表示大正方形的面积，由两个结果相等即可得出结论；
②利用①中的等式直接代入求得答案即可；
（4）根据长方形的长和宽即可画出图形，将2a+ba+2b展开即可；
（5）①如图3，由图形体积的两种不同表示方法可得等式；
②由等式利用代入法即可求解；
（6）根据两个图形体积相等即可列出恒等式．
【详解】（1）解：这体现的数学思想是数形结合；
故选：D；
（2）解：由题意得阴影部分的面积a−b2=a2−2ab+b2．
故答案为：a−b2=a2−2ab+b2；
（3）解：①∵正方形面积为a+b+c2，
小块四边形面积总和为a2+b2+c2+2ab+2bc+2ac，
∴由面积相等可得：a+b+c2=a2+b2+c2+2ab+2bc+2ac；
故答案为：a+b+c2=a2+b2+c2+2ab+2bc+2ac；
②由①可知a2+b2+c2=a+b+c2−2ab+2bc+2ac，
∵a+b+c=9，ab+bc+ac=26，
∴a2+b2+c2=a+b+c2−2ab+2bc+2ac=81−2×26=29，
故答案为：29；
（4）解：面积为2a+ba+2b的长方形如图所示：
∴2a+ba+2b=2a2+5ab+2b2；
（5）解：①用不同的方法表示这个大正方体的体积，
得到的等式为a+b3=a3+3a2b+3ab2+b3；
②∵a+b=5，ab=6，
∴a3+b3=a+b3−3a2b−3ab2
=a+b3−3aba+b
=125−3×6×5
=125−90
=35．
故答案为：a+b3=a3+3a2b+3ab2+b3；35；
（6）解：左边体积=大正方体的体积−小长方体的体积=x3−x；
右边体积=长方体的体积=xx−1x+1；
∴x3−x=xx−1x+1，
故答案为：x3−x=xx−1x+1．
【点睛】本题考查了多项式乘以多项式，完全平方式的几何背景，掌握完全平方公式的几个特征是正确判断的前提，用代数式表示图形的面积、体积是解决问题的关键．注意应用数形结合思想．
8．（2022春·江苏扬州·七年级统考期末）已知一个各个数位上的数字均不为0的四位正整数M=abcda>c，以它的百位数字作为十位，个位数字作为个位，组成一个新的两位数s，若s等于M的千位数字与十位数字的平方差，则称这个数M为“平方差数”，将它的百位数字和千位数字组成两位数ba，个位数字和十位数字组成两位数dc，并记TM=ba+dc．
例如：6237是“平方差数”，因为62−32=27，所以6237是“平方差数”；
此时T6237=26+73=99．
又如：5135不是“平方差数”，因为52−32=16≠15，所以5135不是“平方差数”．
(1)判断7425是否是“平方差数”？并说明理由；
(2)若M=abcd是“平方差数”，且TM比M的个位数字的9倍大30，求所有满足条件的“平方差数”M．
【答案】(1)是，理由如下
(2)M=8175或5214
【分析】（1）根据“平方差数”的定义计算即可；
（2）由M=abcd是“平方差数”，得a2−c2=10b+d，由TM比M的个位数字的9倍大30，得a+c+10b+d＝30，进而得a+ca−c+1=30，结合分解分数的方法分解并分情况讨论即可．
【详解】（1）解： 7254是“平方差数”．理由如下：
∵72−52=24，
∴7254是“平方差数”．
（2）∵M=abcd是“平方差数”，
∴a2−c2=10b+d，T（M）=10b+a+10d+c，
∵T（M）比M的个位数字的9倍大30，
∴10b+a+10d+c=9d+30，即a+c+10b+d=30，
∴a+c+a2−c2=30，
即a+ca−c+1=30．
∵a+c＞0，a−c+1>1且均为30的正因数，
∴将30分解为2×15或3×10或5×6．
①a+ca−c+1=2×15，
解得a=8c=7，
∵82−72=15，
∴M=8175；
②a+ca−c+1=3×10，
解得a=6c=4，
∵62−42=20，
∴M=6240（舍）；
③a+ca−c+1=5×6，
解得a=5c=0或a=5c=1，
∵52−02=25，52−12=24，
∴M=5205（舍）或5214．
∴M=8175或5214．
【点睛】本题主要考查因式分解的应用，解答的关键是理解“平方差数”，明确条件与所求的关系．
9．（2022秋·江苏南京·七年级校联考期末） 数学中的许多规律不仅可以通过数的运算发现，也可以通过图形的面积发现．
(1)填表：【数的角度】
(2)【形的角度】如图①，在边长为a的正方形纸片上剪去一个边长为b（b＜a）的小正方形，怎样计算图中阴影部分的面积？小明和小红分别用不同的方法计算图中阴影部分的面积．小明的方法：若阴影部分看成大正方形与小正方形的面积差，则阴影部分的面积用代数式表示为 ；小红的方法：若沿图①中的虚线将阴影部分剪开拼成新的长方形（图②），则阴影部分的面积用代数式表示为 ．
(3)【发现规律】猜想：a＋b、 a－b 、a2－b2这三个代数式之间的等量关系是 ．
(4)【运用规律】运用上述规律计算：502－492＋482－472＋462－452…＋22－1．
【答案】(1)5，16
(2)a2−b2,(a+b)(a−b)
(3)a2−b2=(a+b)(a−b)
(4)1275
【分析】(1)a=3，b=-2时，a2−b2=32−(−2)2=5;
a=12,b=13时，a-b=12-13=16．
(2)小空1 大正方形面积为a2，小正方形的面积为b2，作差即可．
小空2 把长方形的长和宽分别用含有a、b的代数式表示出来，再按照长方形面积公式计算即可．
(3)根据第(2)小题发现的规律写出等量关系即可．
(4)每两个数为一组按照根据第（3）小题写出的规律进行变形，问题即可解决．
【详解】（1）
（2）小明的方法:大正方形面积为a2，小正方形的面积为b2，，
∴阴影部分的面积为a2-b2；
小红的方法：长方形的长为a+b，宽为a-b，
∴阴影部分的面积为(a+b)(a-b)．
故答案为：a2−b2,(a+b)(a−b)
（3）a＋b、 a－b 、a2－b2这三个代数式之间的等量关系是a2−b2=(a+b)(a−b)．
（4）502－492＋482－472＋462－452…＋22－1
=(502－492)＋(482－472)＋(462－452 )…＋(22－1)
=(50+49) ×(50-49)+(48+47) ×（48-47）+(46+45) ×(46-45) …+(2+1) ×(2-1)
=50+49+48+47+46+45+…+2+1
=50×（50+1）2
=1275
【点睛】本题是一道综合性题目，通过代数计算填表和面积法两种方式发现规律：平方差公式．然后再运用规律进行计算，提高了学生应用数学的能力，解题的关键是发现规律．
10．（2022春·江苏·七年级期末）配方法是数学中重要的一种思想方法，这种方法是根据完全平方公式的特征进行代数式的变形，并结合非负数的意义来解决一些问题．我们规定：一个整数能表示成a²+b²（a,b是整数）的形式，则称这个数为“完美数”．例如，10是“完美数”、理由：因为10=32+12，所以10是“完美数”．
解决问题：
（1）下列各数中，“完美数”有________（填序号）．
①29； ②48： ③13： ④28．
探究问题：
（2）若a²−4a+8可配方成a−m2+n2（m,n为常数），则mn的值________；
（3）已知S=a2+4ab+5b2−8b+k（a,b是整数，k是常数），要使S为“完美数”，试求出符合条件的一个k值，并说明理由．
拓展应用：
（4）已知实数a,b满足−a2+5a+b−3=0，求a+b的最小值．
【答案】（1）①③；（2）±4；（3）当k=16时，S是完美数，理由见详解；（4）a+b的最小值为−1．
【分析】（1）根据“完美数”的定义分别进行判断即可；
（2）利用配方法进行转化，然后求得对应系数的值；
（3）利用完全平方公式把原式变形，根据“完美数”的定义证明结论；
（4）利用配方法和非负数的性质求得a+b的最小值．
【详解】解：（1）根据题意，
∵29=25+4=52+22，13=9+4=32+22，48和28不能拆解为两数的平方和，
∴“完美数”有29和13；
故答案为：①③；
（2）∵a²−4a+8=a2−4a+4+4=(a−2)2+4，
又∵a²−4a+8=a−m2+n2，
∴m=2，n=±2，
∴mn=±4；
故答案为：±4；
（3）当k=16时，S是完美数；
理由如下：
S=a2+4ab+5b2−8b+16
=a2+4ab+4b2+b2−8b+16
=(a+2b)2+(b−4)2；
∵a,b是整数，
∴a+2b和b−4也是整数，
∴当k=16时，S是完美数；
（4）根据题意，
∵−a2+5a+b−3=0，
∴a+b=a2−4a+3，
∴a+b=a2−4a+4−1，
∴a+b=(a−2)2−1，
∵(a−2)2≥0，
∴(a−2)2−1≥−1，
∴a+b的最小值为−1．
【点睛】本题考查了新定义的运算法则，因式分解的应用，配方法的应用，完全平方公式，解题的关键是仔细阅读材料理解分组分解的方法，难度不大．
考点4
二元一次方程组解答期末真题压轴题
1．（2022春·江苏·七年级期末）阅读下列材料：
小明同学在学习二元一次方程组时遇到了这样一个问题：解方程组2x+3y4+2x−3y3=72x+3y3+2x−3y2=8．小明发现，如果用代入消元法或加减消元法求解，运算量比较大，容易出错．如果把方程组中的2x+3y看成一个整体，把2x−3y看成一个整体，通过换元，可以解决问题．以下是他的解题过程：令m=2x−3y，n=2x−3y．原方程组化为m4+n3=7m3+n2=8，解得m=60n=−24，把m=60n=−24代入m=2x−3y，n=2x−3y，得2x+3y=602x−3y=−24，解得x=9y=14，∴原方程组的解为 x=9y=14．
(1)学以致用
运用上述方法解下列方程组：2(x+1)+3(y−2)=1(x+1)−2(y−2)=4．
(2)拓展提升
已知关于x，y的方程组a1x+b2y=c1a2x+b2y=c2的解为x=3y=4，请直接写出关于m、n的方程组a1(m+2)−b2n=c1a2(m+2)−b2n=2的解是 ___________．
【答案】(1)x=1y=1；
(2)m=1n=−4．
【分析】（1）结合题意，利用整体代入法求解，令m=x+1，n=y−2得2m+3n=1m−2n=4，解得m=2n=−1即x+1=2y−2=−1即可求解；
（2）结合题意，利用整体代入法求解，令x=m+2，y=−n则a1(m+2)−b2n=c1a2(m+2)−b2n=2可化为a1x+b2y=c1a2x+b2y=c2，且解为x=3y=4则有m+2=3−n=4，求解即可．
【详解】（1）解：令m=x+1，n=y−2，
原方程组化为2m+3n=1m−2n=4，
解得m=2n=−1，
∴x+1=2y−2=−1，
解得：x=1y=1，
∴原方程组的解为 x=1y=1；
（2）在a1(m+2)−b2n=c1a2(m+2)−b2n=2中，
令x=m+2，y=−n，
则a1(m+2)−b2n=c1a2(m+2)−b2n=2可化为a1x+b2y=c1a2x+b2y=c2，
且a1x+b2y=c1a2x+b2y=c2解为x=3y=4，
则有m+2=3−n=4，
∴m=1n=−4，
故答案为： m=1n=−4．
【点睛】本题考查了解二元一次方程组，整体代入法求解；解题的关键是结合题意理解整体代入法，并正确求解方程组．
2．（2022春·江苏·七年级期末）我们知道，数轴上表示数a的点A和表示数b的点B之间的距离AB可以用a−b来表示．例如：5-1表示5和1在数轴上对应的两点之间的距离．
(1)在数轴上，A、B两点表示的数分别为a、b，且a、b满足a+1+(4−b)2=0，则a=________，b=________，A、B两点之间的距离为________．
(2)点M在数轴上，且表示的数为m，且m+1+4−m=7，求m的值．
(3)若点M、N在数轴上，且分别表示数m和n，且满足m−2022−n=2023，n+2024+m=2025，求M、N两点的距离．
【答案】(1)-1，4，5
(2)m=−2或m=5
(3)4045
【分析】（1）根据绝对值以及偶次方的非负性得出a,b值，运用数轴上两点之间的距离公式进行计算即可；
（2）根据题意可知在数轴上m+1+4−m=7的几何意义是：表示有理数m的点到−1及到4的距离之和为7；然后分m＜−1时、−1≤m≤4时、m>4时分别化简绝对值，解方程即可；
（3）根据题意可得2023+n=±(m−2022)，2025−m=±(n+2024)，然后分情况讨论即可得出答案．
【详解】（1）解：∵ a+1+(4−b)2=0，
∴a+1=0,4−b=0，
解得：a=−1,b=4，
∴A、B两点之间的距离为−1−4=5，
故答案为：-1，4，5；
（2）在数轴上m+1+4−m=7的几何意义是：
表示有理数m的点到−1及到4的距离之和为7，
当m＜−1时，m+1+4−m=−m−1+4−m=7，
解得：m=−2；
当−1≤m≤4时，m+1+4−m=m+1+4−m=7，
无解，故此种情况不存在；
当m>4时，m+1+4−m=m+1+m−4=7，
解得：m=5；
综上所述：m=−2或m=5；
（3）∵m−2022−n=2023，n+2024+m=2025，
∴m−2022=2023+n，n+2024=2025−m，
∴2023+n=±(m−2022)，2025−m=±(n+2024)，
若2023+n=m−20222025−m=n+2024，解得m=2023n=−2022，
此时M、N两点的距离为2023−(−2022)=4045；
若2023+n=−m+20222025−m=n+2024，此方程无解；
若2023+n=m−20222025−m=−n−2024，此方程无解；
若2023+n=−m+20222025−m=−n−2024，解得m=2024n=−2025，
此时m−2022=2023+n=−2＜0，不符合题意；
综上所述：M、N两点的距离为4045．
【点睛】本题考查了绝对值的性质以及数轴上两点之间的距离，根据绝对值的性质得出相应的方程是解本题的关键．
3．（2022春·江苏扬州·七年级统考期末）阅读感悟：有些关于方程组的问题，欲求的结果不是每一个未知数的值，而是关于未知数的一个代数式的值．如以下问题：已知实数x、y满足3x−y=5，2x+3y=7，求x−4y和7x+5y的值．本题常规思路是将3x−y=5①，2x+3y=7②联立组成方程组，解得x、y的值再代入欲求值的代数式得到答案．常规思路计算量比较大，其实本题还可以仔细观察两个方程未知数系数之间的关系，通过适当变形整体求得代数式的值，如由①－②可得x−4y=−2，由①＋②×2可得7x+5y=19．这样的解题思想就是通常所说的“整体思想”．
解决问题：
(1)已知二元一次方程组2x+y=4x+2y=5，则x−y=______，x+y=______；
(2)试说明在关于x、y的方程组x+3y=4−ax−5y=3a中，不论a取什么实数，x+y的值始终不变；
(3)某班级组织活动购买小奖品，买3支铅笔、5块橡皮、1本笔记本共需21元，买4支铅笔、7块橡皮、1本笔记本共需28元，则购买10支铅笔、10块橡皮、10本笔记本共需多少元？
【答案】(1)－1；3
(2)见解析
(3)购买10支铅笔、10块橡皮、10本笔记本共需70元
【分析】（1）①－②可求出x−y，①+②÷3可求出x+y；
（2）证明x+y为定值即可；
（3）设铅笔、橡皮、笔记本的单价分别为x，y，z元，根据题意列方程组，利用整体思想求出x+y+z即可．
【详解】（1）解：2x+y=4①x+2y=5②
①－②得：x−y=−1，
①+②得：3x+3y=9，
等式两边同时除以3得：x+y=3，
故答案为：－1；3．
（2）证明：x+3y=4−a①x−5y=3a②
①+②得：2x−2y=4+2a，
等式两边同时除以2得：x−y=2+a③，
①+③得：2x+2y=6，
等式两边同时除以2得：x+y=3，
因此不论a取什么实数，x+y的值始终不变．
（3）解：设铅笔、橡皮、笔记本的单价分别为x，y，z元，
由题意得，3x+5y+z=21①4x+7y+z=28②
②−①得：x+2y=7，
等式两边同时乘以2得：2x+4y=14③，
①−③得：x+y+z=7，
故10x+10y+10z=70，
即购买10支铅笔、10块橡皮、10本笔记本共需70元．
【点睛】本题考查利用整体思想解方程组，读懂题意，熟练掌握并灵活运用整体思想是解题的关键．
4．（2022春·江苏泰州·七年级泰州市第二中学附属初中校考期末）已知二元一次方程ax+2y−b=0（a，b均为常数，且a≠0）．
(1)当a＝3，b＝﹣4时，用x的代数式表示y；
(2)若x=a−2by=12b2+b是该二元一次方程的一个解，
①探索a与b关系，并说明理由；
②无论a、b取何值，该方程有一组固定解，请求出这组解．
【答案】(1)y=−3x−42
(2)①a=b；②x=1y=0
【分析】（1）直接将a=3，b=−4代入二元一次方程中解关于y的方程即可；
（2）①将方程的解x，y代入原方程中整理可得a−b=0；
②把b=a代入，由取值无关可得a的系数为0，由此即可解题．
【详解】（1）解：当a=3，b=−4时，原方程为：3x+2y+4=0，
∴y=−3x−42；
（2）①a与b关系是a =b，理由：
把x=a−2by=12b2+b代入二元一次方程ax+2y−b=0得
aa−2b+b2+b−b=0，
a2−2ab+b2=0，
a−b2=0，
a−b=0，
∴a=b；
②由①知道a=b，
∴原方程可化为：ax+2y−a=0，
∴ax−1+2y=0
∵该方程组的解与a与b的取值无关，.
∴x=1y=0．
【点睛】本题主要考查了二元一次方程的解的定义、完全平方公式的应用，“有解必代”是解题的关键．
5．（2022春·江苏·七年级期末）某汽配厂接到一批外贸订单急需大量工人生产某配件，工厂人力资源部门计划招聘一批工人．若3名普工和1名高级技工日生产量共500个，2名普工日生产量与1名高级技工的一样多．
（1）求普工和高级技工日生产量分别是多少个？
（2）调查发现，人才市场资源丰富，增加了熟练工人供工厂选择，且其日生产量是普工的1.5倍，他们的工资如下表所示．为了最大限度提高产量，公司决定拨款9万元（全部用完）聘请三类工人（每类工人至少1人）共18人．人力资源部门应招聘三类工人各多少人，使得日生产最大？求出此时的日生产量．
【答案】（1）100个，200个；（2）人力资源部门应招聘普工6人，熟练工3人，高级技工9人，使得日生产最大，此时的日生产量为2850个．
【分析】（1）设普工和高级技工日生产量分别为x个，y个，根据题意列二元一次方程组解决问题；
（2）设招聘普工a人，熟练工b人，则高级技工（18−a−b）人，根据题意列出二元一次方程，由a,b,18−a−b都是正整数，求得整数解，再根据题意求得最值．
【详解】（1）设普工和高级技工日生产量分别为x个，y个，依题意，得：
3x+y=5002x=y，
解得：x=100y=200，
答：普工和高级技工日生产量分别100个，200个．
（2）设招聘普工a人，熟练工b人，则高级技工（18−a−b）人，由题意得：
3500a+5000b+6000(18−a−b)=90000，
整理得：36=5a+2b，
∵a,b,18−a−b都是正整数，
∴a=2b=13,a=4b=8,a=6b=3
工厂日生产量为：100a+150b+200(18−a−b)=3600+100a+150b−200(a+b)
∴当a+b最小时，工厂日生产量最大，
∴a=6b=3时，工厂日生产量为：
∴高级技工18−a−b=9（人），
3600+100a+150b−200(a+b)
=3600−100a−50b
=3600−600−150
=2850（个）．
答：人力资源部门应招聘普工6人，熟练工3人，高级技工9人，使得日生产最大，此时的日生产量为2850个．
【点睛】本题考查了二元一次方程组的应用，二元一次方程的特殊解，根据题意找到等量关系建立方程（组）是解题的关键．
6．（2022秋·江苏扬州·七年级校考期末）结合数轴与绝对值的知识回答下列问题：
（1）数轴上表示5和1的两点之间的距离是_________，一般地，数轴上表示数m和数n的两点之间的距离等于|m−n|．如果表示数a和-2的两点之间的距离是3，那么a=_________．
（2）若数轴上表示数a的点位于-2与5之间，则|a+2|+|a−5|的值为_________．
（3）若x表示一个有理数，且|x−1|+|x+3|>4，则有理数x的取值范围__________．
（4）若将数轴折叠，使得1表示的点与-3表示的点重合，此时M、N两点也互相重合，若数轴上M、N两点之间的距离为2020（M在N的左侧），则M、N两点表示的数分别是M：_______；N：_______．
【答案】（1）4，1或−5；（2）7；（3）x<−3或x>1；（4）1009，−1011
【分析】（1）用5减去1得到距离，然后根据题意列绝对值方程求出a的值；
（2）根据数轴上点与点之间的距离理解|a+2|+|a−5|，得到它的值；
（3）根据数轴上点与点之间的距离理解x−1+x+3，得到当表示数x的点在1和-3两点之外时，能够满足|x−1|+|x+3|>4；
（4）根据题意列式m+n2=−1m−n=2020，解方程组得到结果．
【详解】解：（1）5−1=4，
a−−2=3，解得a=1或−5，
故答案是：4，1或−5；
（2）|a+2|+|a−5|表示数轴上表示数a的点到数轴上表示-2的点和到表示5的点的距离之和，
∵数轴上表示数a的点位于-2与5之间，
∴距离和就是-2和5之间的距离7，
故答案是：7；
（3）x−1+x+3表示数轴上表示数x的点到数轴上表示-3的点和到表示1的点的距离之和，
-3和1之间的距离刚好是4，所以要使距离之和大于4，那么表示数x的点要么在-3的左侧要么在1的右侧，
∴x<−3或x>1，
故答案是：x<−3或x>1；
（4）数轴折叠，1表示的点与-3表示的点重合，则1和-3的中点-1是折叠点，
设点M表示的数是m，点N表示的数是n，
列式m+n2=−1m−n=2020，解得m=1009n=−1011，
故答案是：1009，−1011．
【点睛】本题考查数轴上点与点之间的距离，解题的关键是理解数轴上点与点之间的距离的求解公式并且掌握列方程组求解的方法．
7．（2022春·江苏苏州·七年级期末）已知关于x，y的方程组x+2y−6=0x−2y+mx+5=0
(1)请直接写出方程x＋2y－6＝0的所有正整数解；
(2)若方程组的解满足x＋y＝0，求m的值；
(3)无论实数m取何值时，方程x－2y＋mx＋5＝0总有一个固定的解，求出这个解．
(4)若方程组的解中x恰为整数，m也为整数，求m的值．
【答案】（1）x=2y=2， x=4y=1（2）m=−136（3）x=0y=2.5（4）m=−1或-3
【分析】（1）先对方程变形为x=6-2y，然后可带入数值求解；
（2）把已知的x+y=0和方程x+2y-6=0组合成方程组，求解方程组的解，然后代入方程x-2y+mx+5=0即可求m的值；
（3）方程整理后，根据无论m如何变化，二元一次方程组总有一个固定的解，列出方程组，解方程组即可；
（4）先把m当做已知求出x、y的值，然后再根据整数解进行判断即可.
【详解】（1）x=2y=2 x=4y=1
（2）x+y=0x+2y−6=0 解得x=−6y=6
把x=−6y=6代入x−2y+mx+5=0，解得m=−136
（3）x=0y=2.5
（4）x+2y−6=0①x−2y+mx+5=0②
①+②得：2+mx=1
解得x=12+m，
∵x恰为整数，m也为整数，
∴2+m=1或2+m=-1,
解得m=−1或-3
8．（2022春·江苏·七年级期末）阅读以下内容：
已知有理数m，n满足m+n＝3，且3m+2n=7k−42m+3n=−2求k的值．
三位同学分别提出了以下三种不同的解题思路：
甲同学：先解关于m，n的方程组3m+2n=7k−42m+3n=−2，再求k的值；
乙同学：将原方程组中的两个方程相加，再求k的值；
丙同学：先解方程组m+n=32m+3n=−2，再求k的值．
（1）试选择其中一名同学的思路，解答此题；
（2）在解关于x，y的方程组a+1x−by=18①b+2x+ay=1②时，可以用①×7﹣②×3消去未知数x，也可以用①×2+②×5消去未知数y．求a和b的值．
【答案】（1）见解析；（2）a和b的值分别为2，5．
【分析】（1）分别选择甲、乙、丙，按照提示的方法求出k的值即可；
（2）根据加减消元法的过程确定出a与b的值即可．
【详解】解：（1）选择甲，3m+2n=7k−4①2m+3n=−2②，
①×3﹣②×2得：5m＝21k﹣8，
解得：m＝21k−85，
②×3﹣①×2得：5n＝2﹣14k，
解得：n＝2−14k5，
代入m+n＝3得：21k−85+2−14k5＝3，
去分母得：21k﹣8+2﹣14k＝15，
移项合并得：7k＝21，
解得：k＝3；
选择乙，
3m+2n=7k−4①2m+3n=−2②，
①+②得：5m+5n＝7k﹣6，
解得：m+n＝7k-65，
代入m+n＝3得：7k-65＝3，
去分母得：7k﹣6＝15，
解得：k＝3；
选择丙，
联立得：m+n=3①2m+3n=−2②，
①×3﹣②得：m＝11，
把m＝11代入①得：n＝﹣8，
代入3m+2n＝7k﹣4得：33﹣16＝7k﹣4，
解得：k＝3；
（2）根据题意得：a+1=3b+2=7，
解得：b=5a=2，
检验符合题意，
则a和b的值分别为2，5．
【点睛】此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．
9．（2022春·江苏盐城·七年级校考期末）[阅读材料]
善于思考的小明在解方程组2x+5y=3(1)4x+11y=5(2)时，采用了一种“整体代换”的解法：
解：将方程(2)变形：4x+10y+y=5，
即22x+5y+y=5(3)，
把方程(1)代入(3)得：2×3+y=5，
所以y=−1，
将y=−1代入(1)得x=4，
所以原方程组的解为x=4y=−1．
[解决问题]
（1）模仿小明的“整体代换”法解方程组3x−2y=59x−4y=19，
（2）已知x，y满足方程组3x2−2xy+12y2=50x2+xy+4y2=25，求x2+4y2的值．
【答案】（1）原方程组的解为x=3y=2；（2）x2+4y2=20
【分析】（1）根据题意，利用整体的思想进行解方程组，即可得到答案；
（2）根据题意，利用整体的思想进行解方程组，即可得到答案．
【详解】解：1 3x−2y=5①9x−4y=19②
将方程②变形得:33x−2y+2y=19③
把方程①代入③得:3×5+2y=19，
所以y=2,
将y=2代入①得x=3，
所以原方程组的解为x=3y=2；
2 3x2−2xy+12y2=50①x2+xy+4y2=25②，
把方程①变形，得到3(x2+xy+4y2)−5xy=50 ③，
然后把②代入③，得3×25−5xy=50，
∴xy=5，
∴x2+4y2=25−5=20；
【点睛】本题考查了方程组的“整体代入”的解法．整体代入法，就是变形组中的一个方程，使该方程左边变形为另一个方程的左边的倍数加一个未知数的形式，整体代入，求出一个未知数，再代入求出另一个未知数．
10．（2022春·江苏泰州·七年级校联考期末）用若干块如左图所示的正方形或长方形纸片拼成图（1）和图（2）
（1）如图（1），若AD＝7，AB＝8，求a与b的值；
（2）如图（1），若长方形ABCD的面积为35，其中阴影部分的面积为20，求长方形ABCD的周长；
（3）如图（2），若AD的长度为5，AB的长度为n．
①当m＝________，n＝_________时，a，b的值有无数组；
②当m________，n_________时，a，b的值不存在．
【答案】（1） a＝3，b＝2；（2） C＝24；（3）① m＝4，n＝10；② m＝4，n≠10
【分析】（1）根据图（1）长方形ABCD的边长组成列方程即可解答；
（2）由图（1）中空白部分面积＝大长方形面积－阴影部分面积＝5个小长方形面积，可得ab＝3，再结合完全平方公式可得（a＋b）2＝16，即可得a＋b＝4，而长方形ABCD的周长＝2（3a＋3b），由此即可解答；
（3）由长方形的长和宽可列出关于a、b的方程组，解关于a、b即可解答．
【详解】解：（1）由图得a+2b=72a+b=8，
解得：a=3b=2；
（2）由图可得：5个小长方形面积＝长方形ABCD的面积－阴影部分的面积，
∴5ab=35−20，
∴ab＝3，
∵阴影部分的面积为20，
∴2a2+b2=20，
∴a+b2=16，
∴a＋b＝4，
方形ABCD的周长＝2[（2a＋b）＋（2b＋a）]＝6（a＋b）＝6×4＝24；
（3）由图（2）得：
a+2b=5，①2a+mb=n，②，
由①得a＝5－2b，③
将③代入②得2（5－2b）＋mb＝n，
∴（m－4）b＝n－10，
∴当m−4=0n−10=0 时，a，b的解有无数组；
即m＝4，n＝10时，a，b的值有无数组；
当m−4=0n−10≠0时，方程组无解，
即m＝4，n≠10时，a，b的值不存在
故答案为：①m＝4，n＝10；②m＝4，n≠10．
【点睛】此题主要考查了二元一次方程组的应用，解题关键是弄清题意，找到合适的等量关系，列出方程组．解决本题需仔细观察图形，发现大长方形的边长与a、b之间的关系是关键．讨论方程组的解情况是本题的难点．
考点5
一元一次不等式解答期末真题压轴题
1．（2022春·江苏南通·七年级校考期末）新定义：若一元一次方程的解在一元一次不等式组解集范围内，则称该一元一次方程为该不等式组的“相依方程”，例如：方程x−1=3的解为x=4，而不等式组x−1>1x−2<3的解集为21x−2<3的“相依方程”．
(1)在方程①6(x+2)−(x+4)=23；②9x−3=0；③2x−3=0中，不等式组{2x−1>x+13(x−2)−x≤4的“相依方程”是________；（填序号）
(2)若关于x的方程3x−k=6是不等式组3x+12>xx−12≥2x+13−1的“相依方程”，求k的取值范围；
(3)若关于x的方程x−3m2=−2是关于x的不等式组{x+1>mx−m≤2m+1的“相依方程”，且此时不等式组有5个整数解，试求m的取值范围．
【答案】(1)①
(2)−9(3)32【分析】（1）分别解三个一元一次方程与不等式组，再根据新定义作判断即可；
（2）分别解不等式组与方程，再根据新定义列不等式组−1（3）先解不等式组可得m−132, 从而可得答案．
【详解】（1）解：①6(x+2)−(x+4)=23，
整理得：5x=15, 解得：x=3,
②9x−3=0，
解得：x=13,
③2x−3=0，
解得：x=32.
{2x−1>x+13(x−2)−x≤4
解不等式2x−1>x+1可得：x>2,
解不等式3(x−2)−x≤4可得：x≤5,
所以不等式组的解集为：2根据新定义可得：方程①是不等式组的“相依方程”．
故答案为：①
（2）解：{3x+12>x①x−12≥2x+13−1②
由①得：x>−1,
由②得：x≤1,
所以不等式组的解集为：−1∵ 3x−k=6，
∴x=k+63
根据“相依方程”的含义可得：
−1∴−3解得：−9（3）解：{x+1>m①x−m≤2m+1②
由①得：x>m−1,
由②得：x≤3m+1,
∴不等式组的解集为：m−1此时不等式组有5个整数解，
令整数的值为：n,n+1,n+2,n+3,n+4,
∴{n−1≤m−1∴{n≤m则{n解得：0∴{1≤m<243≤m<53,
∴43≤m<53,
因为x−3m2=−2，
解得：x=3m−4,
根据“相依方程”的含义可得：{m−1<3m−43m−4≤3m+1,
解m−1<3m−4可得：m>32,
而3m−4≤3m+1恒成立，
所以不等式组的解集为：m>32,
综上：32【点睛】本题考查了解一元一次不等式组，一元一次方程的解，理解材料中的不等式组的“相依方程”是解题的关键．
2．（2022春·江苏·七年级期末）【发现问题】已知{3x+2y=4①2x−y=6②，求4x+5y的值．
方法一：先解方程组，得出x，y的值，再代入，求出4x+5y的值．
方法二：将①×2−②，求出4x+5y的值．
【提出问题】怎样才能得到方法二呢？
【分析问题】
为了得到方法二，可以将①×m+②×n，可得(3m+2n)x+(2m−n)y=4m+6n．
令等式左边(3m+2n)x+(2m−n)y=4x+5y，比较系数可得{3m+2n=42m−n=5，求得{m=2n=−1．
【解决问题】
（1）请你选择一种方法，求4x+5y的值；
（2）对于方程组{3x+2y=42x−y=6利用方法二的思路，求7x−7y的值；
【迁移应用】
（3）已知{1≤2x+y≤24≤3x+2y≤7，求x−3y的范围．
【答案】（1）2；（2）26；（3）−38≤x−3y≤−6
【分析】（1）利用方法二来求4x+5y的值；由题意可知4x+5y=2×4−1×6=2；
（2）先根据方法二的基本步骤求出{m=−1n=5，即可得7x−7y=−(3x+2y)+5(2x−y)；
（3）通过方法二得出x−3y=11(2x+y)−7(3x+2y)，再利用不等式的性质进行求解．
【详解】解：（1）利用方法二来求4x+5y的值；
由题意可知：2(3x+2y)−(2x−y)=6x+4y−2x+y=4x+5y，
即4x+5y=2×4−1×6=2；
（2）对于方程组{3x+2y=4①2x−y=6②，
由①×m+②×n可得：(3m+2n)x+(2m−n)y=7x−7y，
则{3m+2n=7③2m−n=−7④，
由③+2×④可得：7m=−7，
∴m=−1，
将m=−1代入④可得n=5，
∴{m=−1n=5，
则7x−7y=−(3x+2y)+5(2x−y)=−1×4+5×6=26；
（3）已知{1≤2x+y≤24≤3x+2y≤7，
通过方法二计算得：
x−3y=11(2x+y)−7(3x+2y)，
又∵11≤11(2x+y)≤22,−49≤−7(3x+2y)≤−28，
∴−38≤x−3y≤−6．
【点睛】本题考查了二元一次方程的求解、代数式的求值、不等式的性质，解题的关键是理解材料中的方法二中的基本操作步骤．
3．（2022春·江苏·七年级期末）若关于x的方程ax+b＝0（a≠0）的解与关于y的方程cy+d＝0（c≠0）的解满足﹣1≤x﹣y≤1，则称方程ax+b＝0（a≠0）与方程cy+d＝0（c≠0）是“友好方程”．例如：方程2x﹣1＝0的解是x＝0.5，方程y﹣1＝0的解是y＝1，因为﹣1≤x﹣y≤1，方程2x﹣1＝0与方程y﹣1＝0是“友好方程”．
（1）请通过计算判断方程2x﹣9＝5x﹣2与方程5（y﹣1）﹣2（1﹣y）＝﹣34﹣2y是不是“友好方程”．
（2）若关于x的方程3x﹣3+4（x﹣1）＝0与关于y的方程3y+k2+y＝2k+1是“友好方程”，请你求出k的最大值和最小值．
【答案】（1）是；（2）k的最小值为﹣23，最大值为83
【分析】（1）分别解出两个方程，得到x﹣y的值，即可确定两个方程是“友好方程”；
（2）分别解两个方程为x＝1，y=3k+25，再由已知可得﹣1≤1−3k+25≤1，求出k的取值范围为即可求解．
【详解】解：（1）由2x﹣9＝5x﹣2，解得x＝−73，
由5（y﹣1）﹣2（1﹣y）＝﹣34﹣2y，解得y＝﹣3，
∴x﹣y＝23，
∴﹣1≤x﹣y≤1，
∴方程2x﹣9＝5x﹣2与方程5（y﹣1）﹣2（1﹣y）＝﹣34﹣2y是“友好方程”；
（2）由3x﹣3+4（x﹣1）＝0，解得x＝1，
由3y+k2+y=2k+1，解得y=3k+25，
∵两个方程是“友好方程”，
∴﹣1≤x﹣y≤1，
∴﹣1≤1−3k+25≤1，
∴−23≤k≤83
∴k的最小值为﹣23，最大值为83．
【点睛】本题主要考查了解一元一次方程和解一元一次不等式组，解题的关键在于能够熟练掌握相关知识进行求解.
4．（2022春·江苏·七年级期末）对于三个数a，b，c，Ma , b , c表示a，b，c这三个数的平均数，mina , b , c表示a，b，c这三个数中最小的数，如：
M−1 , 2 , 3=−1+2+33=43，min−1 ,2 , 3=−1；
M−1 , 2 , a=−1+2+a3=a+13，min−1 , 2 ,a=a a≤−1−1 a>−1．
解决下列问题：
（1）填空：min−22 , 2−2, 20130=______；
（2）若min2 , 2x+2 ,4−2x=2，求x的取值范围；
（3）①若M2 , x+1 , 2x=min2 ,x+1 , 2x，那么x=______；
②根据①，你发现结论“若Ma , b , c=mina ,b , c，那么______”（填a，b，c大小关系）；
③运用②解决问题：若M2x+y+2 , x+2y , 2x−y=min2x+y+2 , x+2y , 2x−y，求x+y的值．
【答案】（1）−4；（2）0≤x≤1；（3）①1，②a=b=c，③−4
【分析】（1）先求出−22,2−2,20130这些数的值，再根据运算规则即可得出答案；
（2）先根据运算规则列出不等式组，再进行求解即可得出答案；
（3）根据题中规定的Ma , b , c表示a，b，c这三个数的平均数，mina , b , c表示a，b，c这三个数中最小的数，列出方程组即可求解．
【详解】（1）∵−22=−4,2−2=14,20130=1，
∴min−22,2−2,20130=−4，
故答案为：-4；
（2）由题意得： 2x+2≥24−2x≥2，
解得：0≤x≤1，
则x的取值范围是：0≤x≤1；
（3）M2 , x+1 , 2x=2+x+1+2x3=x+1=min2 ,x+1 , 2x，
∴x+1≤2x+1≤2x，
∴x≤1x≥1，
∴x=1；
若Ma , b , c=mina ,b , c，则a=b=c；
根据得：
2x+y+2=x+2y=2x−y，
解得：x=−3,y=−1，
则x+y=−4，
故答案为：1，a=b=c．
【点睛】本题考查了一元一次不等式组的应用，解题关键是读懂题意，根据题意结合方程和不等式去求解，考查综合应用能力．
5．（2022春·江苏·七年级期末）我们把关于x的一个一元一次方程和一个一元一次不等式组合成一种特殊组合，且当一元一次方程的解正好也是一元一次不等式的解时，我们把这种组合叫做“有缘组合”；当一元一次方程的解不是一元一次不等式的解时，我们把这种组合叫做“无缘组合”．
（1）请判断下列组合是“有缘组合”还是“无缘组合”，并说明理由；
①2x−4=05x−2＜3；
②x−53=2−3−x2x+32−1＜3−x4．
（2）若关于x的组合5x+15=03x−a2＞a是“有缘组合”，求a的取值范围；
（3）若关于x的组合5a−x2−3=2x−3ax−a2+1≤x+a是“无缘组合”；求a的取值范围．
【答案】（1）①组合是“无缘组合”，②组合是“有缘组合”；（2）a＜-3；（3）a<813
【分析】（1）先求方程的解，再解不等式，根据“有缘组合”和“无缘组合“的定义，判断即可；
（2）先解方程和不等式，然后根据“有缘组合”的定义求a的取值范围；
（3）先解方程和不等式，然后根据“无缘组合”的定义求a的取值范围．
【详解】解：（1）①∵2x-4＝0，
∴x=2，
∵5x-2＜3，
∴x＜1，
∵2不在x＜1范围内，
∴①组合是“无缘组合”；
②x−53=2−3−x2，
去分母，得：2（x-5）＝12-3（3-x），
去括号，得：2x-10＝12-9+3x，
移项，合并同类项，得：x＝-13．
解不等式x+32−1<3−x4，
去分母，得：2（x+3）-4＜3-x，
去括号，得：2x+6-4＜3-x，
移项，合并同类项，得：3x＜1，
化系数为1，得：x＜13．
∵-13在x＜13范围内，
∴②组合是“有缘组合”；
（2）解方程5x+15＝0得，
x＝-3，
解不等式3x−a2>a，得：
x＞a，
∵关于x的组合5x+15=03x−a2>a是“有缘组合”，
∴-3在x＞a范围内，
∴a＜-3；
（3）解方程5a−x2−3=2x−3a，
去分母，得5a-x-6＝4x-6a，
移项，合并同类项，得：5x＝11a-6，
化系数为1得：x＝11a−65，
解不等式x−a2+1≤x+a，
去分母，得：x-a+2≤2x+2a，
移项，合并同类项，得：x≥-3a+2，
∵关于x的组合5a−x2−3=2x−3ax−a2+1≤x+a是“无缘组合，
∴11a−65<-3a+2，
解得：a<813．
【点睛】本题考查一元一次不等式组和新定义，关键是对“有缘组合”与“无缘组合”的理解．
6．（2022春·江苏·七年级期末）对x、y定义了一种新运算T，规定Tx,y=ax+by2x+y（其中a，b均为非零常数），这里等式右边是通常的四则运算，例如：T0,1=a×0+b×12×0+1，
已知T1,−1=−2，T4,2=1．
（1）求a，b的值；
（2）求T−2,2．
（3）若关于m的不等式组T2m,5−4m≤4Tm,3−2m>p恰好有4个整数解，求p的取值范围．
【答案】（1）a=1，b=3；（2）−2；（3）−113≤p<−2．
【分析】（1）根据题中的新定义列出关于a与b的方程组，求出方程组的解即可得到a与b的值；
（2）利用题中的新定义将x=−2，y=2代入计算即可；
（3）利用题中的新定义化简已知不等式组，表示出解集，由不等式组恰好有4个整数解，确定出p的范围，再解不等式组即可．
【详解】解：（1）根据题意得：
a−b=−2①4a+2b2×4+2=1②，
解得：a=1b=3；
（2）由（1）得：Tx,y=x+3y2x+y
∴T−2,2=−2+3×22×(−2)+2=−2；
（3）根据题意得：2m+35−4m4m+5−4m⩽4①m+33−2m2m+3−2m>p②，
由①得：m⩾−12；由②得：m<9−3p5，
∴不等式组的解集为−12⩽m<9−3p5，
∵不等式组恰好有4个整数解，即m=0，1，2，3，
∴3<9−3p5⩽4，
解得：−113≤p<−2．
【点睛】此题考查了解二元一次方程组以及一元一次不等式组的整数解，熟练掌握运算法则、理解新定义的意义是解本题的关键．
7．（2022春·江苏盐城·七年级统考期末）对x，y定义一种新运算T，规定：T（x，y）=ax+2by﹣1（其中a、b均为非零常数），这里等式右边是通常的四则运算，例如：T（0，1）=a•0+2b•1﹣1=2b﹣1．
（1）已知T（1，﹣1）=﹣2，T（4，2）=3．
①求a，b的值；
②若关于m的不等式组{T(2m,5−4m)≤4T(m，3−2m)>p恰好有2个整数解，求实数p的取值范围；
（2）若T（x，y）=T（y，x）对任意实数x，y都成立（这里T（x，y）和T（y，x）均有意义），则a，b应满足怎样的关系式？
【答案】（1）①a=1，b=3；②-2≤p＜-13；（2）a=2b．
【分析】（1）①按题意的运算可得方程组{a−2b−1=−24a+4b−1=3，即可求得a、b的值；
②按题意的运算可得不等式组，即可求得p的取值范围；
（2）由题意可得ax+2by-1= ay+2bx-1，从而可得a="2b" ；
【详解】（1）①由题意可得{a−2b−1=−24a+4b−1=3 ，解得；
②由题意得，解得 ，因为原不等式组有2个整数解，所以， 所以 ；
（2）T（x，y）="ax+2by-1," T（y，x）="ay+2bx-1" ，
所以ax+2by-1= ay+2bx-1,
所以（a-2ba）x-（a-2b）y=0,（a-2b）（x-y）=0,
所以a=2b
8．（2022春·江苏扬州·七年级校考期末）对x，y定义一种新运算T，规定：Tx,y=ax+2by−1（其中a,b均为非零常数），这里等式右边是通常的四则运算，例如：T0,1=a·0+2b·1−1=2b−1．
（1）已知T（1，1）=4，T（4，-2）=7．
①求a、b的值；
②若关于m的不等式组T2m,5−4m<5Tm,3−2m≥p恰好有4个整数解，求实数p的取值范围；
（2）若Tx,y=Ty,x对任意实数x、y都成立（这里Tx,y和Ty,x均有意义），则a、b应满足怎样的关系式？
【答案】（1）①a=3b=1；②−2【分析】（1）①根据规定Tx,y=ax+2by−1将T（1，1）=4，T（4，-2）=7代入求算即可；
②根据①的结果得到关于m的不等式组，再根据恰好有4个整数解得出关于p的不等式组，从而求解；
（2）根据①中结果将Tx,y=Ty,x建立相应的等量关系，从而求解．
【详解】解：（1）①∵Tx,y=ax+2by−1，T（1，1）=4，T（4，-2）=7代入得：
a+2b−1=44a−4b−1=7 解得：a=3b=1
②由①得：Tx,y=3x+2y−1
∴T2m,5−4m<5Tm,3−2m≥p代入得：6m+25−4m−1<53m+23−2m−1≥p
解得：2∵不等式组恰好有4个整数解
∴6≤5−p<7
∴−2（2）∵Tx,y=ax+2by−1
∴Ty,x=ay+2bx−1
又∵Tx,y=Ty,x对任意实数x、y都成立
∴ax+2by−1=ay+2bx−1即：a−2bx=a−2by
∴a=2b．
【点睛】本题考查定义新运算与参数不等式、二元一次方程组等结合，正确理解定义以及参数不等式的求算解题关键．
9．（2022春·江苏无锡·七年级校考期末）对非负实数x“四舍五入”到个位的值记作，即：当n为非负整数时，若n－12≤x＜n＋12，则=n．如：<0>=<0.48>=0，<0.64>=<1.493>=1，<2>=2，<3.5>=<4.12>=4，….
（1）填空：
①<π>=_____；
②如果<2x－1>=3，则实数x的取值范围为_______；
（2）举例说明＝＋不恒成立；
（3）求满足=43x的所有非负实数x的值．
【答案】（1）3；74≤x<94；（2）见解析；（3）0、34、32．
【分析】（1）①π的十分位为1，应该舍去，所以精确到个位是3；
②如果精确数是3，那么这个数应在2.5和3.5之间，包括2.5，不包括3.5，让2.5≤2x-1＜3.5，解不等式即可；
（2）举出反例说明即可，譬如稍微超过0.5的两个数相加；
（3）43x为整数，设这个整数为k，易得这个整数应在应在k-12和k+12之间，包括k-12，不包括k+12，求得整数k的值即可求得x的非负实数的值；
【详解】解：（1）①∵π≈3.14，
∴<π>=3；
②由题意得：2.5≤2x-1＜3.5，解得：
74≤x＜94；
（2）举反例：＜0.6＞+＜0.7＞=1+1=2，而＜0.6+0.7＞=＜1.3＞=1，
∴＜0.6＞+＜0.7＞≠＜0.6+0.7＞，
∴＜x+y＞=＜x＞+＜y＞不一定成立；
（3）∵x≥0，43x为整数，设43x=k，k为整数，
则x＝34k，
∴＜34k＞＝k，
∴k−12≤34k＜k+12，k≥0，
∵0≤k≤2，
∴k=0，1，2，
∴x=0，34，32．
【点睛】考查了一元一次不等式组的应用，解决本题的关键是理解：对非负实数x“四舍五入”到个位的值记为＜x＞，即：当n为非负整数时，如果n-12≤x＜n+12，则＜x＞=n．
a
b
a＋b
a－b
a2－b2
2
1
3
1
3
3
－2
1
5

12
13
56

536
a
b
a＋b
a－b
a2－b2
2
1
3
1
3
3
－2
1
5
5
12
13
56
16
536
工人
普工
熟练工
高级技工
工资（元/人）
3500
5000
6000