初中数学北师大版八年级下册1 等腰三角形试讲课备课课件ppt

这是一份初中数学北师大版八年级下册1 等腰三角形试讲课备课课件ppt，文件包含精选备课北师大版数学八年级下册11等腰三角形2课件pptx、精选备课北师大版数学八年级下册11等腰三角形2教案doc、精选备课北师大版数学八年级下册11等腰三角形2练习doc、精选备课北师大版数学八年级下册11等腰三角形2学案doc等4份课件配套教学资源，其中PPT共22页， 欢迎下载使用。

1.等腰三角形的两腰相等；2.等腰三角形的两底角相等（等边对等角）；3.等腰三角形顶角的平分线，底边上的中线及底边上的高线互相重合；4.等腰三角形是轴对称图形。
想一想：等腰三角形都有哪些性质呢？
1、等腰三角形的两底角相等.（等边对等角）
2、等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合(三线合一).
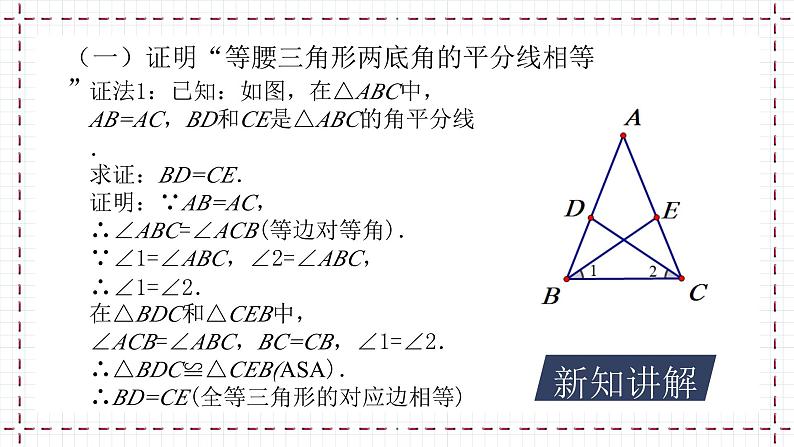
（一）证明“等腰三角形两底角的平分线相等”
证法1：已知：如图，在△ABC中，AB=AC，BD和CE是△ABC的角平分线．求证：BD=CE．证明：∵AB=AC，∴∠ABC=∠ACB(等边对等角)．∵∠1=∠ABC，∠2=∠ABC，∴∠1=∠2．在△BDC和△CEB中，∠ACB=∠ABC，BC=CB，∠1=∠2．∴△BDC≌△CEB(ASA)．∴BD=CE(全等三角形的对应边相等)
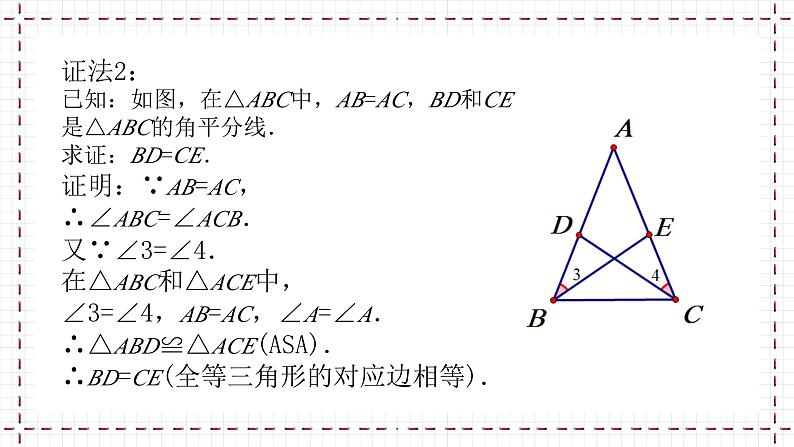
证法2：已知：如图，在△ABC中，AB=AC，BD和CE是△ABC的角平分线．求证：BD=CE．证明：∵AB=AC，∴∠ABC=∠ACB．又∵∠3=∠4．在△ABC和△ACE中，∠3=∠4，AB=AC，∠A=∠A．∴△ABD≌△ACE(ASA)．∴BD=CE(全等三角形的对应边相等)．
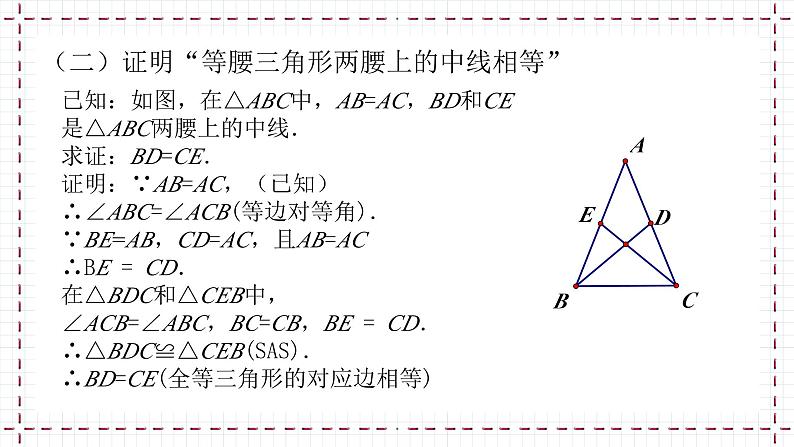
（二）证明“等腰三角形两腰上的中线相等”
已知：如图，在△ABC中，AB=AC，BD和CE是△ABC两腰上的中线．求证：BD=CE．证明：∵AB=AC，（已知）∴∠ABC=∠ACB(等边对等角)．∵BE=AB，CD=AC，且AB=AC∴BE = CD．在△BDC和△CEB中，∠ACB=∠ABC，BC=CB，BE = CD．∴△BDC≌△CEB(SAS)．∴BD=CE(全等三角形的对应边相等)
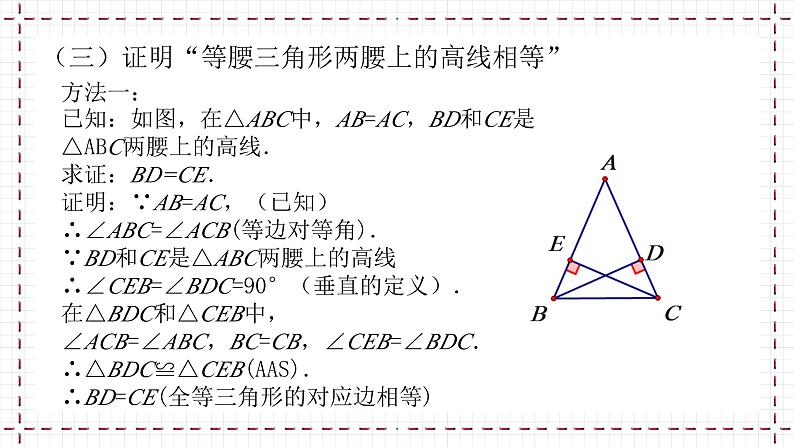
（三）证明“等腰三角形两腰上的高线相等”
方法一：已知：如图，在△ABC中，AB=AC，BD和CE是△ABC两腰上的高线．求证：BD=CE．证明：∵AB=AC，（已知）∴∠ABC=∠ACB(等边对等角)．∵BD和CE是△ABC两腰上的高线∴∠CEB=∠BDC=90°（垂直的定义）．在△BDC和△CEB中，∠ACB=∠ABC，BC=CB，∠CEB=∠BDC．∴△BDC≌△CEB(AAS)．∴BD=CE(全等三角形的对应边相等)
方法二：已知：如图，在△ABC中，AB=AC，BD和CE是△ABC两腰上的高线．求证：BD=CE．证明：∵BD和CE是△ABC两腰上的高线∴∠AEC=∠ADB=90°（垂直的定义）．在△AEC和△ADB中，∠A=∠A，AB=AC，∠AEC=∠ADB．∴△AEC≌△ADB (AAS)．∴BD=CE(全等三角形的对应边相等)
议一议：如图, 在△ABC中, AB=AC, 点D、E分别在边AC和AB上.
(1)如果∠ABD = ∠ABC，∠ACE = ∠ACB，那么BD=CE吗?如果∠ABD = ∠ABC，∠ACE = ∠ACB呢? 由此，你能得到一个什么结论?
在△ABC中，如果AB=AC，∠ABD= ∠ABC，∠ACE= ∠ACB，那么BD=CE.
(2)如果AD= AC，AE= AB，那么BD=CE吗? 如果AD= AC，AE= AB呢? 由此，你能得到一个什么结论?
在△ABC中，如果AB=AC，AD= AC，AE= AB，那么BD=CE.
想一想：等边三角形是特殊的等腰三角形，那么等边三角形的内角有什么特征？
等边三角形的三个内角都相等，并且每个角都等于60°
例2：已知：如图，在△ABC中，AB=AC=BC.求证：∠A=∠B=∠C=60°.证明：∵AB=AC， ∴∠B=∠C(等边对等角). 又∵AC=BC， ∴∠A=∠B(等边对等角). ∴∠A=∠B=∠C. 在△ABC中， ∵∠A+∠B+∠C＝180°， ∴∠A=∠B=∠C＝60°.
等边三角形的性质：等边三角形的三个内角都相等，并且每个角都等于60°
∵△ABC是等边三角形（或AB=AC=BC），∴∠A=∠B=∠C=60°.
练习3：如图，已知△ABC是等边三角形，D，E，F分别是三边AB，AC，BC上的点，且DE⊥AC，EF⊥BC，DF⊥AB，计算△DEF各个内角的度数．
解：∵△ABC 是等边三角形，∴∠A＝∠B＝∠C＝60°.∵DE⊥AC，EF⊥BC，DF⊥AB，∴∠AED＝∠EFC＝∠FDB＝90°.∴∠ADE＝90°－∠A＝90°－60°＝30°.∴∠EDF＝180°－30°－90°＝60°.同理可得∠DEF＝∠EFD＝60°.即△DEF 各个内角的度数都是60°.
如图,已知△ABC和△BDE都是等边三角形,求证:AE=CD
∵ △ABC和△BDE都是等边三角形
∴AB=BC,∠ABC=∠DBE=60°,BE=BD
∴ △ABE≌△CBD
1.求等边三角形两条中线相交所成锐角的度数。2.如图，在△ABC中，D，E是BC的三等分点，且△ADE是等边三角形，求∠BAC的度数。
如图，已知△ABC为等边三角形，延长BC到D，延长BA到E，并且使AE＝BD，连接CE，DE，求证：EC＝ED．
证明：∵△ABC 为等边三角形，∴∠B＝60°，AB＝BC.如图以BE 为边，∠B 为内角作等边三角形BEF.∴BE＝BF＝EF，∠F＝60°.∵AE＝BD，∴BE－AE＝BF－BD，
即AB＝DF.∴BC＝DF.在△ECB和△EDF中，BE＝FE，∠B＝∠F＝60°，BC＝FD，∴△ECB≌△EDF(SAS)．∴EC＝ED.
1、说一说等腰三角形的特殊性质？
（1）等腰三角形两底角的平分线相等；（2）等腰三角形两腰上的中线相等；（3）等腰三角形两腰上的高相等.
2、说一说等边三角形的性质？
（1）等边三角形的三边都相等；（2）等边三角形的三个内角都相等，并且每个角都等于60°.
各边上的高、中线、对应的角平分线重合，且长度相等．
基础作业教材第7页习题1.2第1、3题能力作业教材第7页习题1.2第4题