江西省赣州市经开区2023-2024学年九年级上学期期中数学试题（原卷+解析）

这是一份江西省赣州市经开区2023-2024学年九年级上学期期中数学试题（原卷+解析），文件包含精品解析江西省赣州市经开区2023-2024学年九年级上学期期中数学试题原卷版docx、精品解析江西省赣州市经开区2023-2024学年九年级上学期期中数学试题解析版docx等2份试卷配套教学资源，其中试卷共27页， 欢迎下载使用。
一、选择题（本大题有6小题，每小题3分，共计18分，每小题只有一个正确答案）
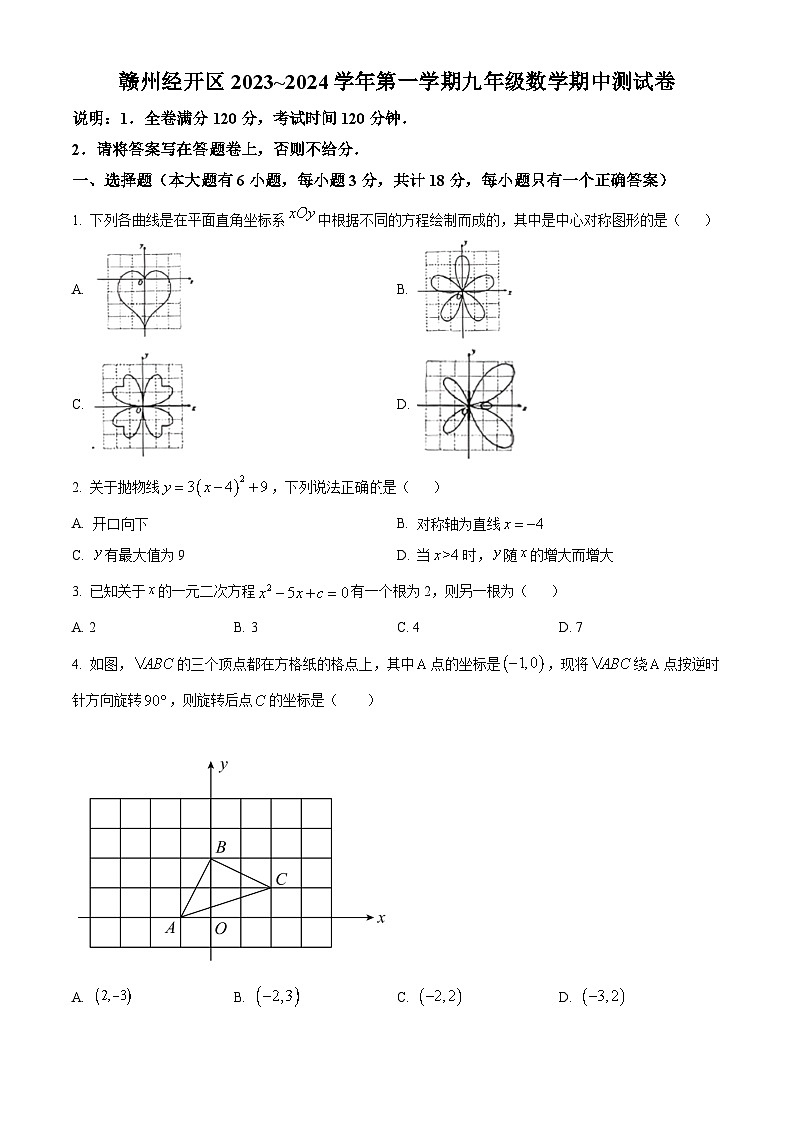
1. 下列各曲线是在平面直角坐标系中根据不同的方程绘制而成的，其中是中心对称图形的是（ ）
A. B.
C. D.
【答案】C
【解析】
【分析】此题主要考查了中心对称图形的概念．在同一平面内，如果把一个图形绕某一点旋转180度，旋转后的图形能和原图形完全重合，那么这个图形就叫做中心对称图形．这个旋转点，就叫做中心对称点．
中心对称图形是要寻找对称中心，旋转180度后与原图重合．根据中心对称图形的概念求解．
【详解】解： A、是轴对称图形不是中心对称图形，故此选项不符合题意；
B、是轴对称图形不是中心对称图形，故此选项不符合题意；
C、是轴对称图形也是中心对称图形，故此选项符合题意；
D、是轴对称图形不是中心对称图形，故此选项不符合题意；
故选：C．
2. 关于抛物线，下列说法正确的是（ ）
A. 开口向下B. 对称轴为直线
C. 有最大值为9D. 当时，随的增大而增大
【答案】D
【解析】
【分析】本题主要考查了二次函数的图象和性质，根据二次函数的图象和性质，逐项判断即可求解．
【详解】解：A、，则抛物线开口向上，故本选项错误，不符合题意；
B、抛物线的对称轴为直线，故本选项错误，不符合题意；
C、函数有最大小值为9，故本选项错误，不符合题意；
D、当时，随的增大而增大，故本选项正确，符合题意；
故选：D
3. 已知关于的一元二次方程有一个根为2，则另一根为（ ）
A. 2B. 3C. 4D. 7
【答案】B
【解析】
【分析】设方程的另一根为，利用一元二次方程的根与系数的关系得到，然后解一元一次方程即可．
【详解】解：设方程的另一根为，
∴，
∴．
故选：B．
【点睛】本题考查了一元二次方程的根与系数的关系：如果一元二次方程的两根分别为，，则，．
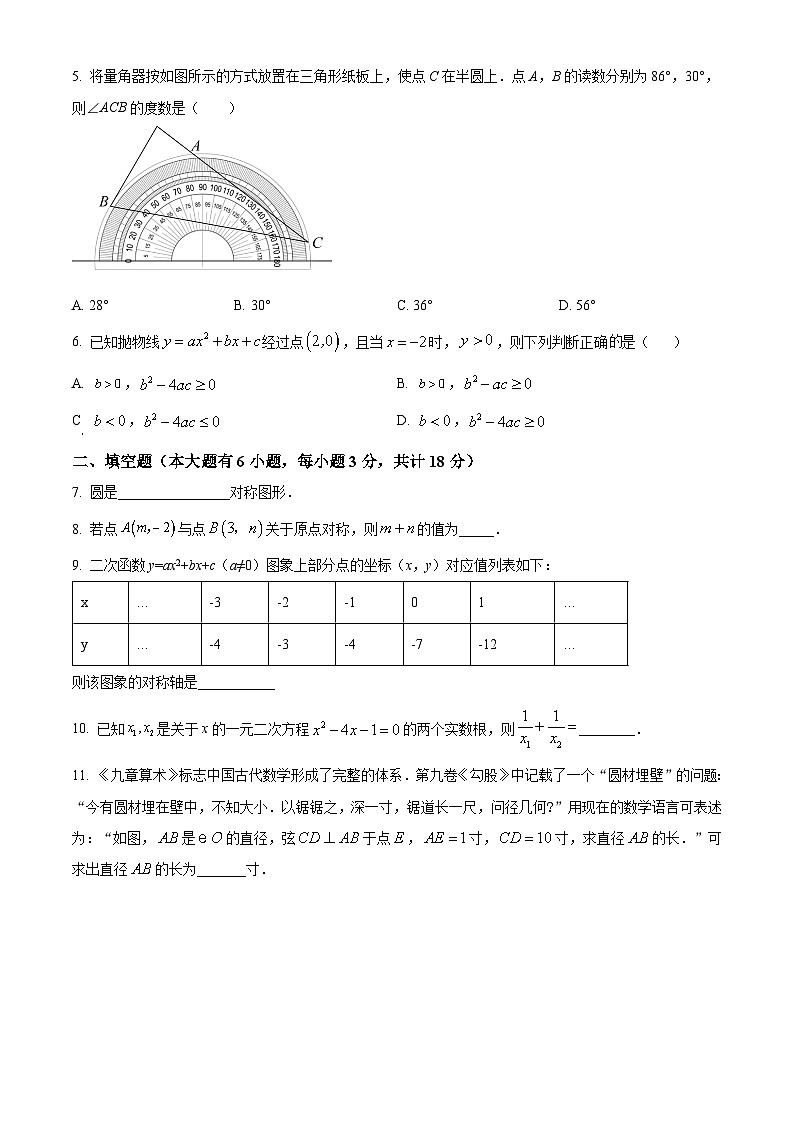
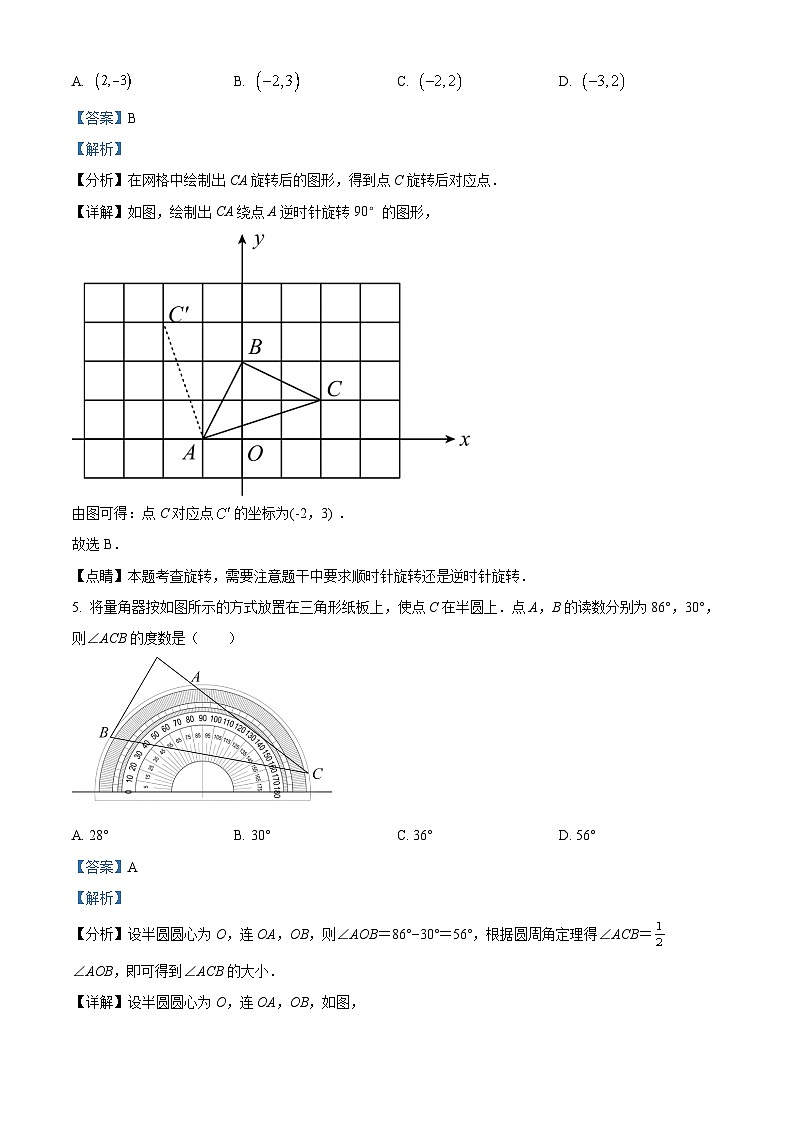
4. 如图，的三个顶点都在方格纸的格点上，其中点的坐标是，现将绕点按逆时针方向旋转，则旋转后点的坐标是（ ）
A. B. C. D.
【答案】B
【解析】
【分析】在网格中绘制出CA旋转后的图形，得到点C旋转后对应点．
【详解】如图，绘制出CA绕点A逆时针旋转90°的图形，
由图可得：点C对应点的坐标为(-2，3) ．
故选B．
【点睛】本题考查旋转，需要注意题干中要求顺时针旋转还逆时针旋转．
5. 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A，B的读数分别为86°，30°，则∠ACB的度数是（ ）
A. 28°B. 30°C. 36°D. 56°
【答案】A
【解析】
【分析】设半圆圆心为O，连OA，OB，则∠AOB＝86°−30°＝56°，根据圆周角定理得∠ACB＝∠AOB，即可得到∠ACB的大小．
【详解】设半圆圆心为O，连OA，OB，如图，
∵∠AOB＝86°−30°＝56°，
∴∠ACB＝∠AOB＝×56°＝28°．
故选A．
【点睛】本题主要考查了圆周角定理．在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
6. 已知抛物线经过点，且当时，，则下列判断正确的是（ ）
A. ，B. ，
C. ，D. ，
【答案】D
【解析】
【分析】由抛物线经过点且当时，，代入解析式即可求解b的范围；根据题意可得抛物线与x轴与两个交点，由二次函数与一元二次方程的关系可得．
【详解】抛物线经过点
当时，
由题意得，抛物线与x轴与两个交点
故选：D．
【点睛】本题考查了二次函数点的坐标的特征、二次函数与一元二次方程的关系，熟练掌握知识点是解题的关键．
二、填空题（本大题有6小题，每小题3分，共计18分）
7. 圆是________________对称图形．
【答案】轴或中心
【解析】
【分析】本题考查了圆的性质，中心对称图形与轴对称图形，根据轴对称图形和中心对称图形的定义判断即可，如果一个平面图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形就叫做轴对称图形；把一个图形绕着某一个点旋转，如果旋转后的图形能够与原来的图形重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．
【详解】圆是轴对称图形，也是中心对称图形．
故答案为：轴或中心．
8. 若点与点关于原点对称，则的值为_____．
【答案】
【解析】
【分析】直接利用两个点关于原点对称时，它们的坐标符号相反，即点关于原点的对称点是，即可得出答案．
【详解】解：点与点关于原点对称，
，
，
故答案为：．
【点睛】本题主要考查了关于原点对称点的性质，正确记忆横纵坐标符号是解题的关键．
9. 二次函数y=ax2+bx+c（a≠0）图象上部分点的坐标（x，y）对应值列表如下：
则该图象的对称轴是___________
【答案】
【解析】
【分析】根据二次函数的图象具有对称性和表格中的数据，可以计算出该函数图象的对称轴．
详解】解：由表格可得，当x取-3和-1时，y值相等，
该函数图象的对称轴为直线，
故答案为：．
【点睛】本题考查二次函数的性质、二次函数图象上点的坐标特征，解题的关键是明确题意，利用二次函数的对称性解答．
10. 已知是关于x的一元二次方程的两个实数根，则________．
【答案】
【解析】
【分析】利用根与系数的关系求出x1+x2与x1x2，原式通分并利用同分母分式的加法法则计算，将各自的值代入计算即可求出值．
【详解】解：∵x1，x2是关于x的一元二次方程x2－4x－1＝0的两个实数根，
∴x1+x2＝4，x1•x2＝－1，
则原式4．
故答案为：－4．
【点睛】本题考查了一元二次方程根与系数的关系，熟练掌握根与系数的关系是解题的关键．
11. 《九章算术》标志中国古代数学形成了完整的体系．第九卷《勾股》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小．以锯锯之，深一寸，锯道长一尺，问径几何?”用现在的数学语言可表述为：“如图，是的直径，弦于点，寸，寸，求直径的长．”可求出直径的长为_______寸．
【答案】26
【解析】
【分析】本题考查了垂径定理、勾股定理，熟练掌握垂径定理是解题关键．连接，设寸，则寸，寸，先根据垂径定理求出寸，再在中，利用勾股定理求解即可得．
【详解】解：如图，连接，
则，
设寸，则寸，寸，
∵是的直径，弦于点，寸，
寸，
在中，，即，
解得，
则寸，
故答案为：26．
12. 在△ABC中，∠C＝90°，∠A＝25°，点O是AB的中点，将OB绕点O向三角形外部旋转角时（0°＜＜180°），得到OP，当△ACP恰为轴对称图形时， 的值为________．
【答案】50°或65°或80°
【解析】
【分析】分三种情形讨论①如图1中，当AC=AP时，②如图2中，当PC=PA时，③如图3中，当CA=CP时，分别利用全等三角形的性质计算即可．
【详解】解：在中，∵∠ACB=90°，AO=OB，
∴OC=OA=OB，
∴∠OAC=∠ACO=25°，∠COB=50°，∠AOC=130°
①如图1中，
当AC=AP时，
在△AOC和△AOP中，
，
∴△AOC≌△AOP，
∴∠AOC=∠AOP=130°，
∴α=∠POB=50°．
②如图2中，当PC=PA时，同理可证△OPA≌△OPC
∴
∴α=∠POB=∠POC-∠COB=65°．
③如图3中，当CA=CP时，
同理可证△COA≌△COB，
∴∠COP=∠AOC=130°，
∴α=∠POB=∠POC-∠COB=80°
故答案为：50°或65°或80°．
【点睛】本题考查旋转变换、全等三角形的判定和性质、直角三角形的性质等知识，解题的关键是学会分类讨论的思想思考问题．
三、解答题（本大题有5小题，每题6分，共计30分）
13. 解方程：
（1）
（2）
【答案】（1），
（2），
【解析】
【分析】本题考查解一元二次方程，正确分解因式是解题的关键．
（1）用因式分解发法求解即可；
（2）先将方程化简整理成一元二次方程的一般式，再用因式分解发法求解即可．
【小问1详解】
解：
或，
∴，．
【小问2详解】
解：，
化简整理，得，
，
或，
∴，．
14. 如图，在边长为3的正方形中，E为边上的一点，连接，将绕点D逆时针方向旋转得到．
（1）旋转角为_____度；
（2）连接，若，求的长．
【答案】（1）
（2）
【解析】
【分析】本题考查旋转的性质，正方形的性质，勾股定理．
（1）由正方形的性质得，再由旋转的性质得，即可得出．
（2）先由勾股定理求得，再证明是等腰直角三角形，然后利用勾股定理求解即可．
【小问1详解】
解：四边形是正方形，
，
∵将绕点D逆时针方向旋转得到．
∴，
∴，
即旋转角为90度；
【小问2详解】
解：四边形是正方形，
，
在中，，
旋转得到，
，
在中，．
15. 已知一次函数的图象与二次函数的图象相交于点，．
（1）求二次函数的表达式；
（2）结合图象，直接写出当时x的取值范围．
【答案】（1）
（2）或
【解析】
【分析】本题主要考查二次函数和一次函数的图象及性质．
（1）先把代入，得出点B的坐标，然后用待定系数法即可求出二次函数的表达式．
（2）另，，要使，即，的函数图像在的函数图像上方，结合函数图像即可解题．
【小问1详解】
把代入，
得，
，
把分别代入，
得，解得，
二次函数解析式为；
【小问2详解】
由（1）可得出，
另，
要使，
即，的函数图像在的函数图像上方，
结合函数图像可知，当或时可满足．
16. 如图，点A、B、C在⨀O上，∠ACB＝125°．请仅用无刻变的直尺分别按下列要求作图．
（1）在图（1）中，作一个度数为55°的圆周角；
（2）在图（2）中，作一个度数为35°的圆周角．
【答案】（1）见解析；（2）见解析
【解析】
【分析】（1）在优弧上任意取一点D，连接DA，DB即可；
（2）作圆的直径BF，连接CF即可．
【详解】（1）如图(1)，在优弧上任意取一点D，
连接DA，DB，
则∠BDA即为所求；
（2）如图(2)，作圆的直径BE，
连接CE，
则∠ECA即为所求．
【点睛】本题考查了圆中的基本作图，熟练掌握圆的内接四边形性质，直径所对的圆周角是直角是解题的关键．
17. 有一种传染性疾病，蔓延速度极快，据统计，在人群密集的城市里，通常情况下，每天一人能传染给若干人，现有一个人患了这种疾病，经过两轮传染后共有个人患有这种疾病．
（1）设这种疾病每轮传染中平均一个人传染了x个人，则第一轮后共有_______个人患病；第二轮传染中，这些人中的每个人又传染了x个人，第二轮后共有_______个人患病．（用含x的式子表示）
（2）求x的值．
【答案】17. ，
18.
【解析】
【分析】本题考查了一元二次方程的应用，正确理解题意是解题关键．
（1）根据这种疾病每轮传染中平均一个人传染了x个人即可求解；
（2）根据题意可列方程求解．
【小问1详解】
解：∵这种疾病每轮传染中平均一个人传染了x个人，
∴一个人可致使x个人患这种疾病，
∴第一轮后共有个人患病，
同理：第二轮后共有个人患病，
故答案为：，；
小问2详解】
解：列方程，
解方程，得（不合题意，舍去），
故的值为．
四、解答题（本题有3小题，每题8分，共计24分）
18. 已知关于的一元二次方程，其中，，为的三边．
（1）若是方程的根，判断的形状，并说明理由；
（2）若方程有两个相等的实数根，判断的形状，并说明理由．
【答案】（1）等腰三角形，理由见解析
（2）直角三角形，理由见解析
【解析】
【分析】（1）根据方程的解把x=1代入方程得到c﹣b=0，即c=b，于是由等腰三角形的判定即可得到ABC是等腰三角形；
（2）根据根的判别式得出a，b，c的关系，即可根据勾股定理的逆定理判断△ABC的形状．
【小问1详解】
解：把x=1代入方程得，
，
化简得，
则该三角形的形状为等腰三角形．
【小问2详解】
解：由题意可得方程有两个相等的实数根
则的判别式：
化简可得
则该三角形的形状为直角三角形．
【点睛】本题考查了根的判别式以及一元二次方程、等腰三角形的判定、直角三角形的判定，掌握一元二次方程根的判别式是解题的关键．
19. 小磊进行铅球训练，他尝试用数学模型来研究铅球的运动情况．小磊某次试投时，铅球的运动路径可以看作抛物线，铅球从距地面处的点处出手，在距出手点水平距离处达到最高点，最高点距地面的距离为．小磊以地面为轴，出手点所在的铅垂线为轴建立平面直角坐标系如图所示．
（1）求铅球运动路径所在抛物线的函数解析式；
（2）若铅球投掷距离（铅球落地点与出手点的水平距离的长度）不小于，成绩记为优秀，请通过计算，判断小磊此次成绩是否能达到优秀．
【答案】（1）
（2）达到优秀
【解析】
【分析】（1）点坐标为，点坐标为，设该抛物线的表达式为，由此即可求解；
（2）在轴正半轴，令，求出点的坐标，由此即可求解．
【小问1详解】
解：由题意得，点坐标为，点坐标为
设该抛物线的表达式为，将点代入，
，解得，
∴该抛物线的表达式为．
【小问2详解】
解：令，得，
解得，（在轴正半轴，故舍去）
∴点的坐标为，
∵，
∴小磊此次试投的成绩达到优秀．
【点睛】本题主要考查二次函数与实际问题的综合，理解并掌握待定系数法求二次函数解析式，二次函数图形的性质是解题的关键．
20. 如图，A、P、B、C是上的四个点，，且平分．
（1）判断的形状，并证明你的结论；
（2）若的半径为2，求的面积．
【答案】（1）等边三角形，理由见解析
（2）
【解析】
【分析】（1）由角平分线的意义得，再根据在同圆或等圆中，相同的圆周角所对的弧相等，相等的弧所对的圆周角相等得出，最后根据有两个角是60度的三角形是等边三角形证明即可；
（2）连接，并延长，交于点，由等边三角形的性质，进而得出，再根据垂直平分线的性质求出的长度，利用勾股定理求出长，进而求解即可．
【小问1详解】
为等边三角形，理由如下：
平分，，
，
，
为等边三角形；
【小问2详解】
连接，并延长，交于点．
为等边三角形，
，
，
，
，
∵点在的垂直平分线上，
垂直平分，
，
，
，
．
【点睛】本题考查了角平分线的意义，圆周角定理的推论，圆周角定理，等边三角形的判定和性质，勾股定理，垂直平分线的判定和性质，熟练掌握知识点是解题的关键．
五、解答题（本题有2小题，每题9分，共计18分）
21. 观察下列两个数的乘积，说明其中哪个积最大．
．
【观察发现】（1）发现所列各组式子中两个因数的和都为_____________．
【问题解决】（2）若设其中一个因数为（，且为正整数），所列两个数的积为y，请说明哪个积最大，最大值是多少．
【拓展应用】（3）若大于0的a、b满足，求的最小值．
【答案】（1）；（2）取50或51时，最大为2250；（3）8
【解析】
【分析】（1）两因数相加即可；
（2）可将题目中的算式设为的形式，利用二次函数的最值求得结果；
（3）由题意可知，，再次利用二次函数的最值求得结果即可.
【详解】（1），
故答案为：101；
（2）由题意可知，另一个因数为,
则（，且为正整数），
对称轴为，因x是正整数，且，
所以x取50或51时，y最大为2250．
（3）∵,∴，
∴，
当时，有最小值为8．
【点睛】本题主要考查了根据已知归纳规律和二次函数的最值问题，发现规律，运用二次函数的最值证明是解答此题的关键.
22. 取一副三角板按图1拼接，固定三角板ADC(∠ACD＝30°)，将三角板ABC(∠ACB＝45°)绕点A依顺时针方向旋转一定的角度得到三角形ABC′，请问：
（1）如图2，当∠CAC′＝15°时，请你判断AB与CD的位置关系，并说明理由；
（2）如图3，当∠CAC′为多少度时，能使CDBC′？
【答案】（1）；理由见解析
（2）当时，能使．
【解析】
【分析】（1）求出，得出∠BAC=∠C=30，利用内错角相等两直线平行求解；
（2）连接，在中利用三角形内角和定理进行解答即可．
【小问1详解】
解：如图1，
∵，
∴，
∴；
【小问2详解】
解：当时，能使．
理由如下：
延长BA交CD于点E，如图2．
∵，
∴．
∵，
∴．
∵，
∴，
∴ ．
【点睛】本题考查了平行线的判定与性质、三角形内角和定理；熟练掌握平行线的判定和三角形内角和定理，并能进行推理计算是解决问题的关键．
六、解答题（本题12分）
23. 二次函数y＝a（x﹣h）2+k（a≠0）的图象是抛物线，定义一种变换，先作这条抛物线关于原点对称的抛物线y′，再将得到的对称抛物线y′向上平移m（m＞0）个单位，得到新的抛物线ym，我们称ym叫做二次函数y＝a（x﹣h）2+k（a≠0）的m阶变换．
（1）已知：二次函数y＝2（x+2）2+1，它的顶点关于原点的对称点为 ，这个抛物线的2阶变换的表达式为 ．
（2）若二次函数M的6阶变换的关系式为y6′＝（x﹣1）2+5．
①二次函数M的函数表达式为 ．
②若二次函数M的顶点为点A，与x轴相交的两个交点中左侧交点为点B，在抛物线y6′＝（x﹣1）2+5上是否存在点P，使点P与直线AB的距离最短，若存在，求出此时点P的坐标．
（3）抛物线y＝﹣3x2﹣6x+1的顶点为点A，与y轴交于点B，该抛物线的m阶变换的顶点为点C．若△ABC是以AB为腰的等腰三角形,请直按写出m的值．
【答案】（1）（2，﹣1），y＝﹣2（x﹣2）2﹣1；（2）存在，点P（，），（3）8+或8﹣或8或2．
【解析】
【分析】（1）原二次函数的顶点为（-2，1），则顶点关于原点的对称点为（2，-1），即可求解；（2）①6阶变换的关系式对应的函数顶点为：（1，-1），则函数M的顶点为：（-1，1），即可求解；②DP =PH=（x2-2x+6-x-2）=（x2-3x+4），即可求解；
（3）点A（-1，4）、点B（0，1），抛物线的m阶变换的函数表达式为：y=3（x-1）2-4+m，故点C（1，m-4），即可求解．
【详解】解：（1）原二次函数的顶点为（﹣2，1），则顶点关于原点的对称点为（2，﹣1），
则这个抛物线2阶变换的表达式：y＝﹣2（x﹣2）2﹣1，
故答案为（2，﹣1），y＝﹣2（x﹣2）2﹣1；
（2）①6阶变换的关系式对应的函数顶点为：（1，﹣1），则函数M的顶点为：（﹣1，1），
则其表达式为：y＝﹣（x+1）2+1，
故答案为y＝﹣（x+1）2+1；
②存在，理由：
y＝﹣（x+1）2+1，令y＝0，则x＝﹣2或0，
故点B（﹣2，0），而点A（﹣1，1），
将点A、B的坐标代入一次函数表达式：y＝kx+b得：，解得：，
故直线AB的函数表达式为：y＝x+2，
y6′＝（x﹣1）2+5＝x2﹣2x+6，
如下图，过点P作PD⊥AB交于点D，故点P作y轴平行线交AB于点H，
∵直线AB的倾斜角为45°，则DP＝PH，
设点P（x，x2﹣2x+6），则点H（x，x+2），
DP＝PH＝（x2﹣2x+6﹣x﹣2）＝（x2﹣3x+4），
∵＞0，故DP有最小值，此时x＝，
故点P（，）；
（3）抛物线y＝﹣3x2﹣6x+1的顶点为点A，与y轴交于点B，
则点A（﹣1，4）、点B（0，1），
抛物线的m阶变换的函数表达式为：y＝3（x﹣1）2﹣4+m，
故点C（1，m﹣4），
则AB2＝10，AC2＝4+（m﹣8）2，BC2＝1+（m﹣5）2，
当AB＝AC时，10＝4+（m﹣8）2，解得：m＝8；
当AB＝BC时，同理可得：m＝8或2，
故m的值为：8+或8﹣或8或2．
【点睛】本题考查的是二次函数综合运用，涉及到一次函数、勾股定理的运用等，解决本题的关键是要熟练掌握二次函数、一次函数、勾股定理.
x
…
-3
-2
-1
0
1
…
y
…
-4
-3
-4
-7
-12
…