





沪科版八年级下册18.1 勾股定理教课ppt课件
展开18 .1 勾 股 定 理
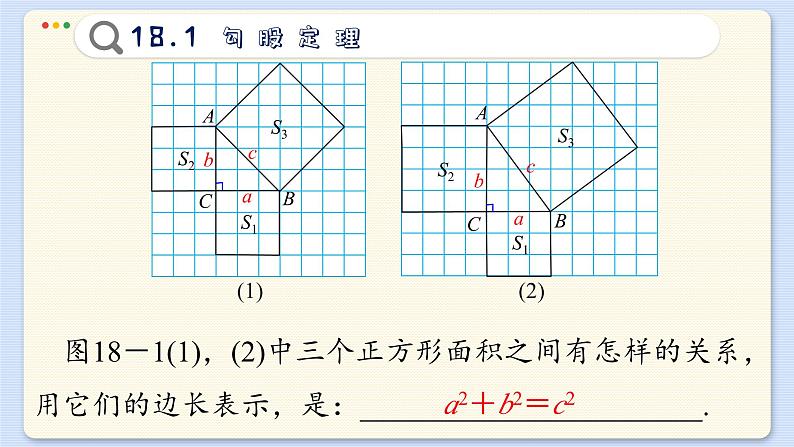
在行距、列距都是1的方格网中,任意作出几个以格点为顶点的直角三角形,分别以三角形的各边为正方形的一边,向形外作正方形,如图18-1.并以S1,S2与S3;分别表示几个正方形的面积.
观察图 18-1(1),并填写:
S1=__________个单位面积;S2=__________个单位面积;S3=__________个单位面积.
观察图 18-1(2),并填写:
图18-1(1),(2)中三个正方形面积之间有怎样的关系,用它们的边长表示,是:_______________________.
通过上面的探究,你能发现直角三角形三边的长之间有怎样的关系吗?
直角三角形两条直角边的平方和,等于斜边的平方.
我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦. 因此,我们称上述定理为勾股定理国外称为毕达哥拉斯定理.
如果直角三角形的两直角边用 a,b表示,斜边用 c 表示,那么勾股定理可表示为
a2 + b2 = c2 .
已知:如图18-2(1),在 Rt△ABC 中∠C =90°,AB =c,BC =a,AC = b.
求证:a2 + b2 = c2.
下面,用面积计算来证明这个定理.
证明 取4个与 Rt△ABC 全等的直角三角形,把它们拼成如图 18-2(2)所示的边长为 a+b的正方形 EFGH .
从图中可见,A1B1= B1C1 =C1D1=A1D1=c.因为∠B1A1E + ∠A1B1E =90°,而 ∠A1B1E = ∠D1A1H,因此∠B1A1E + ∠D1A1H = 90°, ∠D1A1B1 = 90°.
同理: ∠A1B1C1 = ∠B1C1D1= ∠C1D1A1 = 90°, 所以四边形A1B1C1D1,是边长为 c的正方形.
正方形 EFGH 和正方形 A1B1C1D1的面积分别记作 S正方形EFGH和 S正方形A1B1C1D1则
S正方形EFGH- 4S△ABC = S正方形A1B1C1D1
a2 + b2 = c2.
例1 现有一楼房发生火灾,消防队员决定用消防车上的云梯救人,如图 .已知云梯最多只能伸长到10m,消防车高 3 m. 救人时云梯伸至最长,在完成从9 m 高处救人后,还要从 12 m 高处救人,这时消防车要从原处再向着火的楼房靠近多少米?(精确到 0.1 m)
分析:如图,设A是云梯的下端点,AB 是伸长后的云梯,B 是第一次救人的地点,D 是第二次救人的地点,过点A的水平线与楼房 ED 的交点为O.则OB =9-3=6(m),OD =12-3=9(m).
AO2=AB2-OB2=102-62=64.
设 AC =x,则 OC =8-x,于是根据勾股定理,得
OC2 + OD2 = CD2,
即 (8-x)2 + 92 = 102,
请根据上述分析写出解题过程.
例2 已知:如图18 - 4,在 Rt△ABC 中两直角边AC = 5,BC = 12. 求斜边上的高 CD 的长.
解 在 Rt△ABC 中,
AB2 = AC2 + BC2 = 52 + 122 = 169,
又∵ Rt△ABC 的面积
1. 在△ABC中,∠C=90°,AB=c,BC=a,AC=b. (1) a = 6,b = 8,求c;
1. 在△ABC中,∠C=90°,AB=c,BC=a,AC=b. (2) a = 8,c = 17,求b.
2. 如图,楼梯的高度为 2 m,楼梯坡面的长度为 4 m,要在楼梯的表面铺上地毯,那么地毯的长度至少需要多少米?(精确到0.1 m)
由题意知:∠C = 90°,AB = 4m,AC = 2m
3.(1) 如图,长3 m的梯子斜靠着墙,梯子 底端离墙底 0.6 m,问梯子顶端离地 面多少米? (精确到 0.1m)
(2) 题(1)中,若梯子的顶端自墙面下滑了 0.9 m,那么梯子的底端沿地面向外滑 动的距离是否也为 0.9 m? 说明理由.
设水池的深度为x尺,由题意得:x2+52= (x+1)2,解得: x=12,则x+1=13.答:水深12尺,芦苇长13尺
长度为正整数的算术平方根的线段,可以用尺规作图的方法作出来.下面介绍一种有趣的方法,你能说出其中的道理吗?
如上继续下去,可以作出长度为任一正整数的算术平方根的线段.
1.在△ABC中,∠C =90°,填空:
(1) 如果AB=10, BC∶AC=3∶4,那么 BC =_______, AC = ______;
(2) 如果 AC =1, ∠B = 30°,那么 AB =_______, BC = _______;
2. 已知:在△ABC中,AB = AC = 17,BC = 16. 求 △ABC的高AD的长.
如图所示∵AB = AC = 17∴△ABC是等腰三角形∵AD是△ABC的高,BC = 16.
3. 已知直角三角形的三边长是三个连续自然数,求三 边长.
设三边长分别为 x-1,x ,x+1由勾股定理可得(x-1)2+x2= (x+1)2解得 x1=0 (舍去) ,x2=4,∴ 三边长分别为 3,4,5.
4. 求边长为 a 的等边三角形的面积.
5. 如图,从电线杆上离地面 h = 8 m 的点 A 处,向地面 拉一条长 l = 12 m 的缆绳,这条缆绳拉直后在地面上 点 B 处固定,点 B 离电线杆底部点C 的距离是多少米? (精确到 0.1 m)
6. 如图,要修一个塑料蔬菜大棚,棚宽 b =3 m,高 h =1.5 m,长l=10 m.求覆盖在顶上的长方形塑料薄膜 需要多少平方米?(精确到 0.1 m2)
7. 如图,在甲村到乙村的公路旁有一块山地正在开发,现有A处需要爆破.已知点 A 与公路上的停靠站 B,C 的距离分别为400 m和300 m,且AC⊥AB. 为了安全起见,如果爆破点A 周围半径 250 m 的区域内不能有车辆和行人,问在进行爆破时,公路 BC 段是否需要暂时封闭?为什么?
数学八年级下册18.1 勾股定理图片ppt课件: 这是一份数学八年级下册18.1 勾股定理图片ppt课件,共15页。PPT课件主要包含了SA+SBSC,千古第一定理,数与形的第一定理,导致第一次数学危机,数学由计算转变为证明,是第一个不定方程,毕达哥拉斯定理,勾股商高定理,有趣的总统证法,想一想等内容,欢迎下载使用。
初中数学沪科版八年级下册第18章 勾股定理18.1 勾股定理备课课件ppt: 这是一份初中数学沪科版八年级下册第18章 勾股定理18.1 勾股定理备课课件ppt,共10页。PPT课件主要包含了SA+SBSC,a2+b2c2,sA+sBsC,求AB的长等内容,欢迎下载使用。
沪科版八年级下册18.1 勾股定理图文课件ppt: 这是一份沪科版八年级下册18.1 勾股定理图文课件ppt,共12页。PPT课件主要包含了探索勾股定理,拼一拼试一试等内容,欢迎下载使用。













