沪科数学8年级下册 第19章 小结与复习 PPT课件

这是一份沪科数学8年级下册 第19章 小结与复习 PPT课件，共60页。

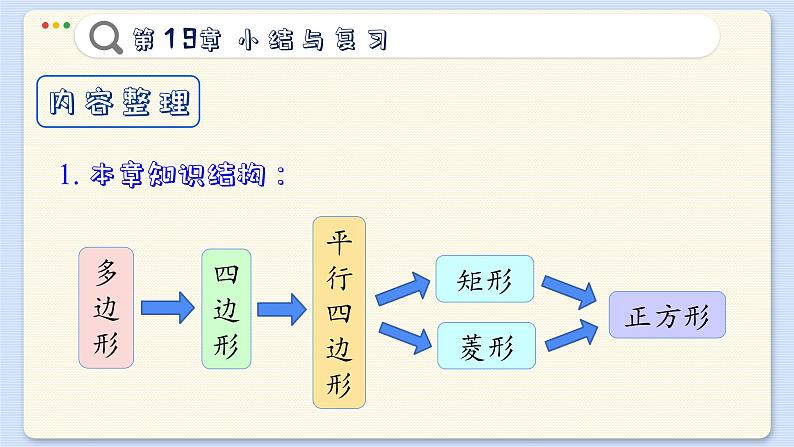
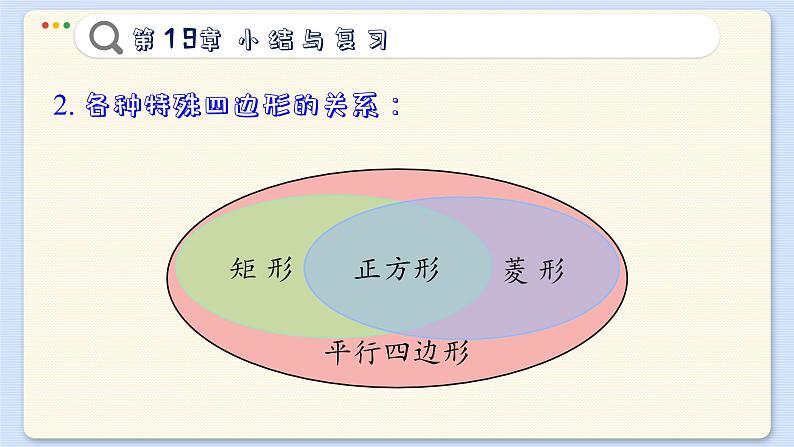
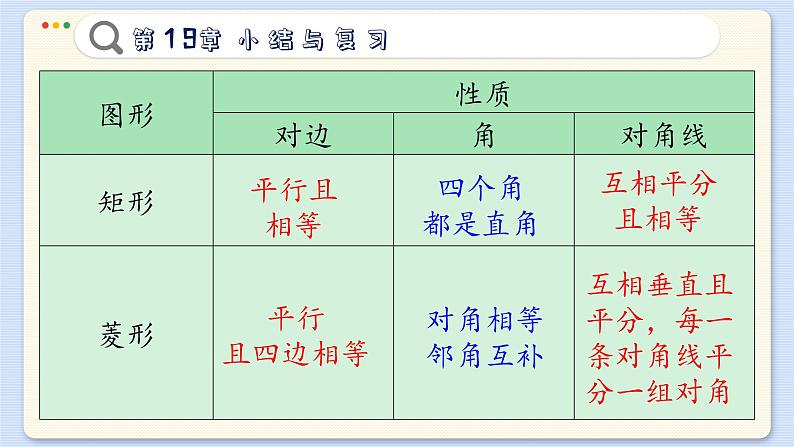
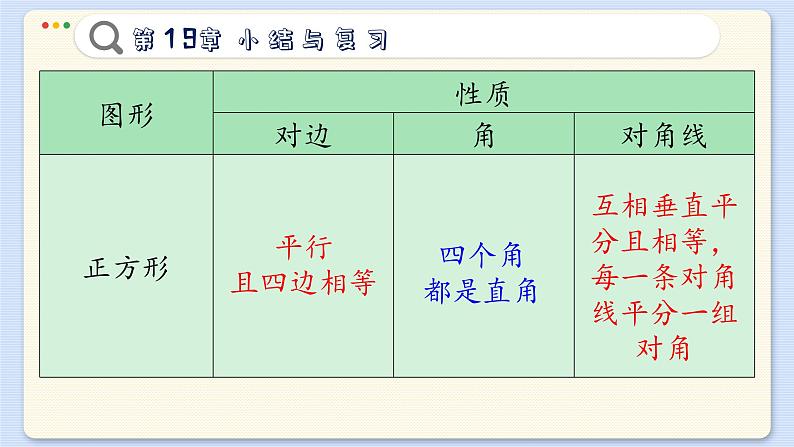
第19章 四边形义务教育沪科版数学八年级下册小结与复习内容整理多边形四边形平行四边形矩形菱形正方形1. 本章知识结构：2. 各种特殊四边形的关系：平行四边形矩 形菱 形正方形主要知识回顾一. 各种特殊四边形的性质.平行且相等对角相等邻角互补互相平分平行且相等四个角都是直角互相平分且相等平行且四边相等对角相等邻角互补互相垂直且平分，每一条对角线平分一组对角平行且四边相等四个角都是直角互相垂直平分且相等，每一条对角线平分一组对角二、如何判定一个四边形是平行四边形、矩形、菱形、 正方形?1. 平行四边形的判定：两组对边相等一组对边平行且相等对角线互相平分两组对边分别平行(定义)2. 矩形的判定：①定义：有一个角是直角的平行四边形.②定理1：对角线相等的平行四边形.③定理2：三个角是直角的四边形.3. 菱形的判定：①定义：一组邻边相等的平行四边形.②定理1：四条边都相等的四边形.③定理2：对角线互相垂直的平行四边形.4. 正方形的判定： ①定义：有一个角是直角且一组邻边相等的平行四边形. ②有一组邻边相等的矩形. ③有一个角是直角的菱形.三、多边形的内角和与外角和多边形的内角和等于 (n - 2)×180°多边形的外角和等于 360°正多边形每个内角的度数是正多边形每个外角的度数是四、三角形的中位线 1. 三角形中位线的定义：连接三角形两边中点的线段叫做三角形的中位线. 2. 三角形中位线定理：三角形两边中点连线平行于第三边，并且等于第三边的一半. 用符号语言表示：∵ DE 是△ABC 的中位线，∴ DE∥BC，复习题 A组 9490°2. 四边形的内角可能都是锐角吗?可能都是直角吗?可能 都是钝角吗? 四边形的四个内角不可以都是锐角，不可以都是钝角，可以都是直角. 因为四边形的内角和为360° 如果四个内角都是锐角或都是钝角则内角和小于360°或大于360°，与四边形的内角和为360°矛盾. 所以四个内角不可以都是锐角或都是钝角. 若四个内角都是直角，则四个内角的和等于360°与内角和定理相符， 所以四个内角可以都是直角.3. 是否存在一个多边形，它的每个内角都等于相邻外角 的3倍?并简述你的理由存在. 设该多边形一个外角为x°，则相邻的内角是3x°， 根据多边形内角和相邻外角的关系(邻补角)得: x°＋3x°＝180°.∴ x＝45，∴ 该多边形边数为：360°÷45°＝8 (多边形外角和定理)，∴ 正八边形的每个内角都等于相邻外角的3倍. 综上所述：存在一个多边形，它的每个内角都等于相邻外角的3倍.证明：∵四边形ABCD是平行四边形. ∴∠A＝∠C，AD＝BC. 又∵ AE＝ CF. ∴ △AED≌△CFB. ∴ DE ＝ BF，∠ADE ＝ ∠CBF. ∵ M、N是ED、BF的中点. ∴ EM＝FN. ∵ AB∥DC. ∴ ∠AED ＝∠CDE又∵ ∠ADE ＝ ∠CBF， ∠ABC ＝ ∠ADC. ∴ ∠ABF ＝ ∠CDE. ∴ ∠AED ＝ ∠ABF. ∴ ED ∥ BF. 即 EM ∥ FN. ∴ 四边形MFNE 是平行四边形(一组对边平行且相等的四边形是平行四边形).证明：∵四边形ABCD是平行四边形. ∴AB ∥ CD. ∴∠CAB ＝ ∠ACD， ∵ O是对角线AC的中点. ∴AO ＝ CO.在△AOF和△COE中 ∠CAB ＝ ∠ACD， CO ＝ AO， ∠EOC ＝ ∠FOA.∴ △COE ≌ △AOF (ASA)，∴ EO ＝ FO.6. 将一张长40 cm宽20 cm 的矩形纸片剪成长为18 cm、 宽为12cm 的矩形纸片，问最多能剪几个?答： 最多可以剪3个. ∵ 20×40 ÷ 18×12 ≈ 3.7. ∴ 结合长和宽可知最多剪3个，如下图.四边形ABEF是菱形.理由：∵四边形ABCD是平行四边形.∴AF ∥ BE∴∠FAE ＝ ∠BEA∵ EF ∥ AB∴ 四边形ABEF是平行四边形∵∠EAF ＝ ∠EAB∴∠BEA ＝ ∠EAB∴ BA ＝ BE∴四边形ABEF是菱形.8. 某地有四个村庄 A，B，C，D，它们正好位于一个正 方形的四个顶点. 现在四个村庄计划联合架设一条电 话线路，他们设计了 4 种架设方案，如图中的实线 部分. 请你帮助计算一下，哪种架设方案最省电线.设正方形的边长为1，则有：(1) 电线长为： AD＋AB＋BC＝1＋1＋1＝3；  (4) 分别过点E，F作EM⊥AD，FN⊥BC 垂足分别为M，N，如图：MN MN    MN  ∵ 2.732 ＜ 2.82 ＜3＜ 3.41，∴第四种最省电线.9. 如图，在正方形 ABCD 中，点 E，F 是边 BC，CD 上 的点，且BE = CF. 那么，线段AE 与 BF的夹角有多大? 为什么?90°.理由如下：在正方形ABCD中，AB ＝ BC，∠ABE ＝∠BCF.∵ BE ＝CF.∴△ABE ≌△BCF∴∠AEB＝ ∠BFC， ∠EAB ＝ ∠FBC.∵∠BFC ＋∠FBC ＝∠AEB ＋∠EAB ＝90°.∴∠AEB ＋∠FBC ＝90°.∴AE ⊥BF.∴线段AE与BF的夹角是90°.复习题 B组1. 一个多边形的内角中，最多有几个锐角?为什么? 一个多边形的内角中，最多有3个锐角. 理由是：因为多边形的外角和是360度，在外角中最多有3个钝角，如果超过3个，则和一定大于360度，多边形的内角与外角互为邻补角. 所以外角中最多有3个钝角，内角中就最多有3个锐角. 证明：连结DE，过点D作DN⊥AE于点N，过点E作EM⊥AD于点M.NM NM在平行四边形中： S□ABCD ＝ AD × EM.在平行四边形中： S□ABFG ＝ AE × DN.∴S□ABCD ＝ S□AEFG.3. 已知：点 M，N分别是 ABCD 的边 AB，CD 的中点 CM交 BD 于点 E，AN 交 BD 于点 F. 求证：BE = EF = FD.证明：在平行四边形ABCD中，∴ AB∥CD，AB＝CD.∴△AFB ~ △NFD.∴DF∶ BF＝DN∶AB，∵N为DC的中点，∴DF∶BF＝DN∶AB＝1∶2， 4. 已知点O是矩形 ABCD 内任一点. 求证：OA2 ＋OC2 ＝ OB2 ＋OD2. 如果点O在矩形ABCD的外部，结论 还成立吗?证明：当O在矩形ABCD的内部时，如图，过O作OM ⊥ AD于M，延长MO交BC于N，则∠AMO ＝ ∠DMO ＝ ∠CNO ＝ ∠ BNO ＝ 90°，∵四边形ABCD是矩形，∴ ∠DAB ＝ ∠ABC ＝ ∠BCD ＝ ∠ADC ＝ 90°，∴ 四边形ABNM和四边形DCNM是矩形，MN∴ AM ＝ BN，DM ＝ CN，由勾股定理得：OA2 ＋ OC2 ＝AM2 ＋ OM2 ＋CN2＋ON2OB2 ＋ OD2 ＝ BN2 ＋ ON2 ＋DM2＋OM2 ∴ OA2＋OC2＝OB2＋OD2；MN当O在矩形ABCD的外部时，OA2＋OC2＝OB2＋OD2 还成立，OO理由是：过O作OM⊥AD于M，延长OM交BC于N，如图，则∠AMN ＝ ∠DMN ＝∠CNM ＝ ∠BNM ＝ 90°，∵四边形ABCD是矩形，∴∠DAB ＝∠ABC ＝∠BCD ＝∠ADC ＝ 90°，MN∴四边形ABNM和四边形DCNM是矩形，∴AM ＝ BN，DM ＝ CN，由勾股定理得：OA2 ＋ OC2 ＝ AM2 ＋ OM2 ＋ CN2＋ON2，OB2＋OD2 ＝ BN2＋ON2 ＋DM2＋OM2.∴OA2＋OC2 ＝ OB2＋OD2.OMN5. 在△ABC 中，BD，CE 是两条高，点P，Q 分别是BC， ED 的中点. 求证：PQ ⊥ED .证明：作出图形， 连结PE、PD. ∴DP ＝ EP.△EPD为等腰三角形.∵Q为ED的中点.∴PQ ⊥ ED. (三线合一)复习题 C组1. 设四边形 ABCD 的每一个顶点到其他 3 个顶点的距离 之和都相等. 这个四边形是什么四边形?请说明理由.四边形ABCD是矩形，理由如下：由题意得， AB＋AD＋AC＝DA＋DB＋DC＝DC＋CB＋AC＝BA＋BC＋BD.∴AB＝CD，AD＝BC，AC＝BD，∴四边形ABCD为矩形2. 证明：在 ABCD中，AC2＋BD2＝2(AB2＋BC2).如图所示：过A作AE⊥BC于E，过D作DF⊥BC，交BC延长线于F，EF ∵四边形ABCD是平行四边形， ∴ AB＝CD，∠ABE ＝∠DCF又∵∠AEB＝∠DFC ＝90° ∴△ABE≌△DCF。 ∴ AE＝DF， BE＝CF ∵AC2 ＝AE2＋CE2＋BF2， BD2＝DF2＋BF2 ∴ AC2＋BD2＝ (AE2＋CE2)＋(DF2＋BF2)＝ AE2＋(BC－BE)2＋AE2＋(BC＋CF)2＝2AE2＋BC2－2BC·BE＋BE2＋BC2 ＋2BC·BE＋BE2＝2AE2＋2BE2 ＋2BC2＝2(AE2＋BE2) ＋2BC2＝2AB2＋2BC2＝2(AB2＋BC2)故在□ABCD中，AC2＋BD2＝2(AB2 ＋ BC2).3. 已知：如图，在矩形内一些相交线把它分成 8 个部分， 其中的3个部分面积分别为 13，35，49. 求图中阴影 部分的面积.xyxy ∵(35 ＋x ＋49) ＋(13 ＋ y) ＝长方形面积的一半，又∵长方形面积的一半＝ x ＋S阴影＋ y， ∴ S阴影＝35＋49 ＋13＝97.4. (1) 如图(1)，从ABCD 的顶点 A，B，C，D，向形外的 任意直线 MN作垂线AA′，BB′，CC′，DD′，垂足是 点A′，B′，C′，D′. 求证：AA′＋ CC′ ＝ BB′ ＋ DD′ .证明： 记点O为平行四边形ABCD两条对角线的交点，作OO′ ⊥ MN，垂足为 O′.OO′∵在平行四边形ABCD中， AO ＝ OC，AA′∥OO′∥CC′，∴OO′是梯形AA′CC′的中位线.∴ OO′ ＝(AA′ ＋ CC′)，同理可证 OO′ ＝(BB′ ＋ DD′).∴ AA′ ＋ CC′ ＝ BB′ ＋ DD′ .OO′(2) 如图(2)，将直线 MN 向上平移，使得点A 在直线一 侧，点 B，C，D 三点在直线的另一侧，这时，从 点 A，B，C，D 向直线 MN作垂线， 垂足分别为点 A′，B′，C′，D′， 那么垂线段AA′，BB′，CC′， DD′之间存在什么关系?CC′＝AA′＋BB′＋DD′ OO′HOO′H (3) 如图(3)，再将直线 MN 向上平行移动，使两侧各有 两个顶点，从点 A，B，C，D向直线 MN作的垂线 段AA′，BB′，CC′，DD′，它们之间 又有什么关系? 根据图(2)、 图(3)写出你的猜想， 并加以证明.AA' ＋ DD′ ＝ BB′ ＋ CC′ OO′HG OO′HG本课结束