沪科数学8年级下册 第20章 小结与复习 PPT课件

这是一份沪科数学8年级下册 第20章 小结与复习 PPT课件，共60页。

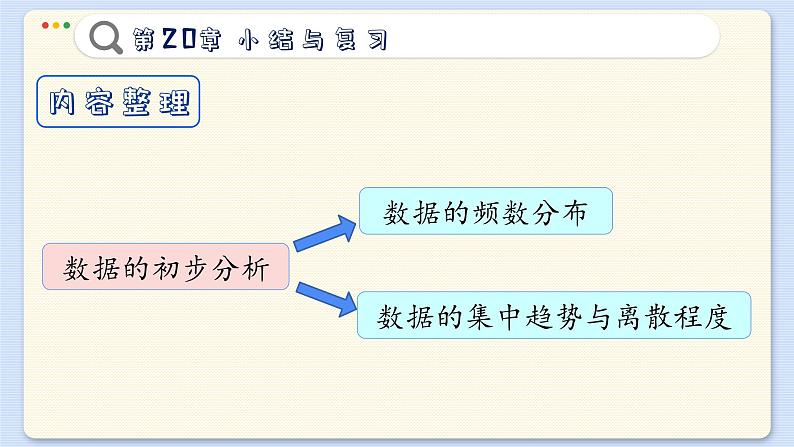
第20章 数据的初步分析义务教育沪科版数学八年级下册小结与复习内容整理数据的初步分析数据的频数分布数据的集中趋势与离散程度主要知识回顾一、数据的集中趋势中间位置的数两个数据的平均数最多二、数据的波动程度大平均数 三、用样本估计总体1．统计的基本思想：用样本的特征(平均数和方差)估 计总体的特征．2．统计的决策依据：利用数据做决策时，要全面、多 角度地去分析已有数据，从数据的变化中发现它们 的规律和变化趋势，减少人为因素的影响．复习题 A组1. 下列数据为某城市2012 年 11 月份每天最高的气温 (单位：C)：30，28，32，27，25，25，26，24，24，26，23，23，21，17，12，16，19，21，22，23，22，24，23，20，21，22，20，19，20，21.先适当分组，列出频数分布表，再绘制频数直方图.频数分布表如下：812≤t＜1616≤t＜20 1 4 20≤t＜24 1424≤t＜28 28≤t＜32232≤t＜361合计30 频数分布直方图如下：12 16 20 24 28 32 3614121086420 气温天数1414821 2. 如图是九年级 2 班学生的一次体检中每分钟心跳次数的频数直方图(次数均为整数). 已知该班只有 5 位学生的心跳每分钟 75 次，请观察图后，指出下列说法是否正确?(1) 数据 75 落在第 2小组；(2)第4 小组的频率为 0.1； 由第2组的范围是69.5~79.5知数据75落在第2小组，故此说法正确；    3. 为了了解学校开展“孝敬父母，从家务事做起”活动的实际情况，该校抽取八年级50名学生，调查他们一周(按 7 天计算)家务所用时间(单位：h)，得到一组数据，并绘制成下表，请根据该表完成下列各题：(1) 填写频数分布表中未完成的部分；频数分布表 (2) 由以上信息判断，每周做家务的时间不超过 1.5 h 的学生所占百分率是_______.58% 4. 希望中学为了解九年级男生的身高情况，抽测了 50 名男生的身高(单位：m)，数据如下： (1) 若将数据分成6组，取组距为 0.04 m，试完成相应的频数分布表：(2) 画出频数直方图；身高(m)人数(人)1.5651.6051.6451.6851.7251.7651.8052420161284024122282 (3) 根据样本数据，身高在 1.695 ~1.755 之间的男生所占的百分率为多少?如果该校九年级共有 450名男生，那么在 1.695~1.755 m之间的人数约有多少人?所占的百分率为：  (3) 根据样本数据，身高在 1.695 ~1.755 之间的男生所占的百分率为多少?如果该校九年级共有 450名男生，那么在 1.695~1.755 m之间的人数约有多少人?人数约有：450 ×44% ＝198(人) 5. 某校为推动信息技术的发展，举行了电脑设计作品比赛，各个班派学生代表参加现将所有比赛成绩(得分取整数，满分为 100 分)进行整理后分成五组，并绘制成如图所示的频数直方图，请根据统计图提供的信息，解答下列问题：(1) 参加比赛的学生代表共有多少人?4＋12＋20＋10＋6＝52(人)(2) 80.5 ~90.5 分这个分数段的频数频率分别是多少?由图示知，80.5 ～90.5分这个分数段的频数是10. (3) 根据统计图，请你提出一个问题，并回答. 问题：若80.5分以上为优秀，问这次电脑设计作品比赛的优秀率约为多少？  6. 某邮局有 A，B，C，D 四名投递员，年终时按职业道德、工作态度、工作能力及工作实绩四个方面进行考核，每一项的满分均为 100 分，得分最高者为本年度先进工作者. 如果各方面的权数及四名投递员的得分如下：问谁是本年度的先进工作者?    ∵ 78 ＜78.1 ＜80 ＜82.6，∴ D为本年度先进工作者.7. 华东地区主要城市某天的最低气温情况如图所示.求这些城市该天最低气温的平均数、中位数和众数.  共有18个城市，气温从小到大排列后处在第9、10位的两个数都是1℃，故中位数是1℃. 最低气温为1℃的城市最多为9个，因此这些城市该天最低气温的众数是1℃； 答：些城市该天最低气温的平均数为1.6℃，中位数是1℃ ，众数是1℃.8. 某班学生百米跑测试成绩如下表所示：求测试成绩的中位数、众数和平均数(精确到 0.1s). 将这些成绩按从小到大的顺序排列，处于最中间的两个成绩为16.5和16.5，所以测试成绩的中位数为 16.5s . 测试成绩中出现次数最多的成绩是16.5，所以测试成绩的众数为16.5s. 9. 甲、乙两台机床同时生产一种零件，在 10 天中，两 台机床每天出的次品数分别是：甲：0，1，0，2，2，0，3，1，2，4；乙：2，3，1，1，0，2，1，1，0，1. 分别计算两组数据的平均数和方差，并说明哪台机床在 10 天中出的次品数波动较大.甲：0，1，0，2，2，0，3，1，2，4；乙：2，3，1，1，0，2，1，1，0，1. 甲：0，1，0，2，2，0，3，1，2，4；乙：2，3，1，1，0，2，1，1，0，1. 甲：0，1，0，2，2，0，3，1，2，4；乙：2，3，1，1，0，2，1，1，0，1. ∵ S甲2 ＝ 1.65 ＞ 0.76 ＝ S乙2 ，∴说明甲机床在10天内出现次品的波动较大.10.甲、乙两台包装机同时包装质量为 200 g 的糖果，从 中分别抽出若干袋，测得其质量(单位：g)如下：甲：203，204，202，196，199，201，205，197， 202，199；乙：201，200，208，210，209，200，193，194.(1) 分别计算两组数据的平均数和方差； (1) 分别计算两组数据的平均数和方差； S甲2＝[(203－200.8)2＋(204－200.8)2＋···＋(199－200.8)2＝ 7.96， S乙2 ＝(201－201.875)2＋(200－201.875)2＋··· ＋(194 － 201.875)2 ＝ 20.42.(2) 从计算结果看，哪台包装机包装的糖果的质量比 较稳定?∵S乙2 ＞ S甲2∴甲包装机包装10袋糖果的质量比较稳定. 11. 要从甲、乙两位车工中选拔一名参加技术比赛. 现从他们加工的零件中各抽取 5 个零件进行检验，测得它们的直径(单位：m)分别为：甲：15.05，15.02，14.97，14.96，15.00；乙：15.00，15.01，15.02，14.97，15.00.问哪位车工的技术发挥较稳定?甲：15.05，15.02，14.97，14.96，15.00；乙：15.00，15.01，15.02，14.97，15.00. 甲：15.05，15.02，14.97，14.96，15.00；乙：15.00，15.01，15.02，14.97，15.00. S甲2 ＝[(15.05－15.00)2＋(15.02－15.00)2＋···＋(15.00－15.00)²]÷5 ＝ 0.00108， S乙2 ＝(15.05－15.00)²＋(15.02－15.00)2＋···＋(15.00－15.00)2÷5 ＝ 0.0014， ∵ S甲2 ＜ S乙2， ∴甲车工的技术发挥较稳定. 12. 某粮店购进东北大米 1000 袋，为了检验每袋大米的质量，从中任意抽取 10 袋大米，称得质量(单位：kg)如下：10，10.2，9.9，10，9.9，9.9，10.1，10，10.1，10.请你估计这批大米的质量.  13. 某鱼塘放养鱼苗 10 万条，根据这几年经验知道，鱼苗成活率为 95%. 一段时间后，准备将鱼打捞出售. 第一次网出 40 条，称得平均鱼重 2.5 kg；第二次网出25条，称得平均鱼重 2.2 g；第三次网出 35 条，称得平均鱼重2.8 kg，请你估计鱼塘中鱼的总质量为多少千克?由题意可得： (40×2.5＋25×2.2＋35×2.8)÷(40＋25＋35)＝2.53(千克)，故10万×95%×2.53 ＝ 240350(千克)，答：鱼塘中的鱼总质量大约是240350千克. 14. 从某灯泡厂生产的一批灯泡中随机地抽取 10 只进行寿命测试，得到数据(单位：h)如下：1 458，1 395，1 562，1 614，1 351，1 490，1 478，1 382，1 536，1 496.试估计这批灯泡的平均寿命及寿命的方差.1 458，1 395，1 562，1 614，1 351，1 490，1 478，1 382，1 536，1 496. 复习题 B组 1.无核柑橘是皖西南山区特产. 小明家有一块成龄无核柑橘园，去年采摘时，小明利用统计知识. 对柑橘的等级和产量进行了测算：他随机选择了若干棵柑橘树，从中共摘得 240个柑橘，并对这些柑橘的直径进行了测量和统计，绘制出如图(1)所示的频数直方图. 已知一级鲜柑橘的直径在 5.5~7.5 cm 之间. (1) 估计柑橘园中一级柑橘所占的比例是多少；   (2) 由于受储存季节的变化等影响，柑橘的售价会随时间的变化而变化，每千克一级柑橘的月平均售价变化情况如图(2). 若小明家去年共摘得一级柑橘4 000 kg. 现请你利用图象提供的信息，计算出小明家的一级橘在 4月份出售时，一共能卖多少钱?(不考虑其他因素对柑橘质量的影响) 小明家的一级柑橘在4月份出售时，一共能卖4000×[1.2＋ (1.6－1.2)÷4×3＝6000(元) 因此小明家的一级柑橘在4月份出售时，一共能卖6000元. 2. 某风景区对 5 个旅游景点的门票价格进行了调整. 据统计，调价前后各景点的客人数基本不变. 有关数据如下表：风景区管理部门：调价前后这 5 个景点门票的平均价格 不变. 因而，就总体而言，风景区在 门票价格调整中没有获益.游客：调整门票价格后风景区的平均日收入相对于调价 前实际增加了 9.4%因此调价对风景区有利.请你分析他们的说法谁符合实际.  3. 公交6 路汽车总站设在一个新开发的居民小区附近，这个小区居民出行主要选乘6 路车为了了解在 7∶00 至8∶00 这个高峰时段内乘该路车的人数，公交公司抽查了 10 个班次的乘车人数，结果如下：25，28，34，36，35，36，32，30，28，26.25，28，34，36，35，36，32，30，28，26.(1) 计算这 10 个班次乘该路车人数的平均数；  (2) 如果在高峰时段从总站发车 20 个班次估计在高峰时段乘该路车的人数.20 × 31 ＝ 620(人)。答：估计在高峰时段乘该路车的人数有620人。 4. 甲、乙两人在相同的条件下各射靶 10 次，每次射靶的成绩如下：甲：9，5，7，8，7，6，8，6，7，7；乙：2，4，6，8，7，7，8，9，9，10.(1) 填写下表：(2) 请从下面 4 个不同的角度对这次测试结果进行分析： ①平均数和方差相结合，分析谁的成绩稳定； 方差反映了一组数据的波动大小，方差越大，波动性越大.甲的成绩稳定；②平均数和中位数相结合，分析谁的成绩好些；平均数和中位数相结合，乙的成绩好些； ③平均数和命中9环以上的次数相结合，分析谁的成绩好些； 平均数与命中9环以上的次数相结合，乙的成绩好些； ④ 作折线统计图，从折线统计图上两人射击命中环数的走势分析，谁更有潜力. 乙有潜力，因为乙后来逐渐稳定，成绩越来越好. 5. 某市林业局于 2005 年对直接从原产地引进的绒毛白蜡树种进行育苗造林，经过3年育苗试验、6 年造林试验获得成功.苗木高、径生长量表 该林业局农艺师根据此表作出分析：“从苗木高、径生长情况看苗木逐年出现分化，且分化程度不断增加，说明播种苗有再选优的必要性和可能性.” (1) 比较同一苗龄两个苗圃苗木高、径的平均数； 由表格中的信息可知：同一苗龄乙苗圃的高，径的平均数比甲苗圃的高，径的平均数值要大. (2) 比较同一苗龄两个苗圃苗木高、径的年平均生长值； 由表格中的信息可知：同一苗龄乙苗圃的高，径年平均生长值比甲苗圃的高，径的值要大. (3)同一苗龄两个苗圃苗木高、径的平均数、方差所反映苗木的差异；由表格中的信息可知：同一苗龄乙苗圃苗木高、径的平均数比甲苗圃苗木高、径的平均数要大，2龄苗，3龄苗乙苗圃苗木高、径的方差比甲苗圃苗木高、径的方差要小. (4) 决定优选哪个苗圃的树苗.由表格中的信息可知：选乙苗圃苗木比较好.复习题 C组 某村为了对甲、乙两名村干部进行年度考核，召开了一次述职答辩及民主测评会. 乡政府派出 A，B，C，D，E 五位评委对“述职答辩”进行评价；并从村里选出 20名村民代表参加民主测评. 结果如表所示： 规定：述职答辩得分“按去掉一个最高分和一个最低分再算平均分”的方法确定： 综合得分 ＝述职答辩得分×(1－a)＋民主测评得分×a (0.5 ≤ a≤0.8). 民主测评得分 ＝ “优秀”票数×5＋“良好”票数×3＋“一般”票数×1； (1)当a ＝0.6时，甲和乙的综合得分分别是多少?  甲民主测评得分＝12 ×5 ＋6 ×3 ＋2 ×1 ＝80(分) 乙民主测评得分＝13 ×5 ＋5 ×3 ＋2 ×1 ＝82(分) 甲的综合得分＝92×(1－a)＋80×a＝92－12a (分)，当a ＝ 0.6 时，甲的综合得分＝ 92 － 12×0.6 ＝84.8 (分)；乙的综合得分＝ 89 － 7×0.6＝84.8 (分). 乙的综合得分＝89×(1－a)＋82×a＝89－7a (分)， (2)甲的综合得分高时，a 在什么范围?乙的综合得分高时，a 又在什么范围?当甲的综合得分高时，有92 － 12a ＞ 89 － 7a，解得：a＜0.6，所以，当0.5＜a＜0.6时，甲的综合得分高;当0.6 ＜a＜0.8时，乙的综合得分高.本课结束