2024年高考数学二轮复习【举一反三】系列 专题3.1 导数的概念及其几何意义与运算【八大题型】- （新高考专用）

这是一份2024年高考数学二轮复习【举一反三】系列 专题3.1 导数的概念及其几何意义与运算【八大题型】- （新高考专用），文件包含专题31导数的概念及其几何意义与运算八大题型举一反三新高考专用原卷版docx、专题31导数的概念及其几何意义与运算八大题型举一反三新高考专用解析版docx等2份试卷配套教学资源，其中试卷共26页， 欢迎下载使用。
一、注意基础知识的整合、巩固。二轮复习要注意回归课本，课本是考试内容的载体，是高考命题的依据。浓缩课本知识，进一步夯实基础，提高解题的准确性和速度
二、查漏补缺，保强攻弱。在二轮复习中，对自己的薄弱环节要加强学习，平衡发展，加强各章节知识之间的横向联系，针对“一模”考试中的问题要很好的解决，根据自己的实际情况作出合理的安排。
三、提高运算能力，规范解答过程。在高考中运算占很大比例，一定要重视运算技巧粗中有细，提高运算准确性和速度，同时，要规范解答过程及书写。
四、强化数学思维，构建知识体系。同学们在听课时注意把重点要放到理解老师对问题思路的分析以及解法的归纳总结，以便于同学们在刷题时做到思路清晰，迅速准确。
五、解题快慢结合，改错反思。审题制定解题方案要慢，不要急于解题，要适当地选择好的方案，一旦方法选定，解题动作要快要自信。
六、重视和加强选择题的训练和研究。对于选择题不但要答案正确，还要优化解题过程，提高速度。灵活运用特值法、排除法、数形结合法、估算法等。
专题3.1 导数的概念及其意义与运算【八大题型】
【新高考专用】
TOC \ "1-3" \h \u
\l "_Tc24472" 【题型1 导数的定义及其应用】 PAGEREF _Tc24472 \h 2
\l "_Tc19161" 【题型2 求（复合）函数的导数的方法】 PAGEREF _Tc19161 \h 3
\l "_Tc3673" 【题型3 求曲线切线的斜率（倾斜角）】 PAGEREF _Tc3673 \h 3
\l "_Tc27454" 【题型4 求在曲线上一点的切线方程、过一点的切线方程】 PAGEREF _Tc27454 \h 4
\l "_Tc30930" 【题型5 已知切线（斜率）求参数】 PAGEREF _Tc30930 \h 4
\l "_Tc21498" 【题型6 切线的条数问题】 PAGEREF _Tc21498 \h 5
\l "_Tc9419" 【题型7 两条切线平行、垂直、重合（公切线）问题】 PAGEREF _Tc9419 \h 5
\l "_Tc431" 【题型8 与切线有关的最值问题】 PAGEREF _Tc431 \h 6
1、导数的几何意义与运算
导数是高考数学的必考内容，是高考常考的热点内容，从近三年的高考情况来看，主要涉及导数的运算及几何意义，一般以选择题、填空题的形式考察导数的几何意义、求曲线的切线方程，导数的几何意义也可能会作为解答题中的一问进行考查，试题难度属中低档.
【知识点1 切线方程的求法】
1.求曲线“在”某点的切线方程的解题策略：
①求出函数y=f(x)在x=x0处的导数，即曲线y=f(x)在点(x0,f(x0))处切线的斜率；
②在已知切点坐标和切线斜率的条件下，求得切线方程为y=y0+f'(x0)(x-x0).
2.求曲线“过”某点的切线方程的解题通法：
①设出切点坐标T(x0,f(x0))(不出现y0)；
②利用切点坐标写出切线方程：y=f(x0)+f'(x0)(x-x0)；
③将已知条件代入②中的切线方程求解.
【知识点2 复合函数的导数】
1.复合函数的定义
一般地，对于两个函数y=f(u)和u=g(x)，如果通过变量u,y可以表示成x的函数，那么称这个函数为函
数y=f(u)和u=g(x)的复合函数，记作y=f(g(x)).
2.复合函数的求导法则
复合函数y=f(g(x))的导数和函数y=f(u),u=g(x)的导数间的关系为 =，即y对x的导数等于y
对u的导数与u对x的导数的乘积.
3.求复合函数导数的步骤
第一步：分层：选择中间变量，写出构成它的内、外层函数；
第二步：分别求导：分别求各层函数对相应变量的导数；
第三步：相乘：把上述求导的结果相乘；
第四步：变量回代：把中间变量代回.
【题型1 导数的定义及其应用】
【例1】（2023下·山东·高二校联考阶段练习）若limΔx→0f(−2+Δx)−f(−2−Δx)Δx=−2，则f′−2=（ ）
A．1B．-1C．2D．-2
【变式1-1】（2022·高二课时练习）设f(x)是可导函数，且limΔx→0f(x0−2Δx)−f(x0)Δx=2，则f′(x0)=（ ）
A．12B．-1C．0D．-2
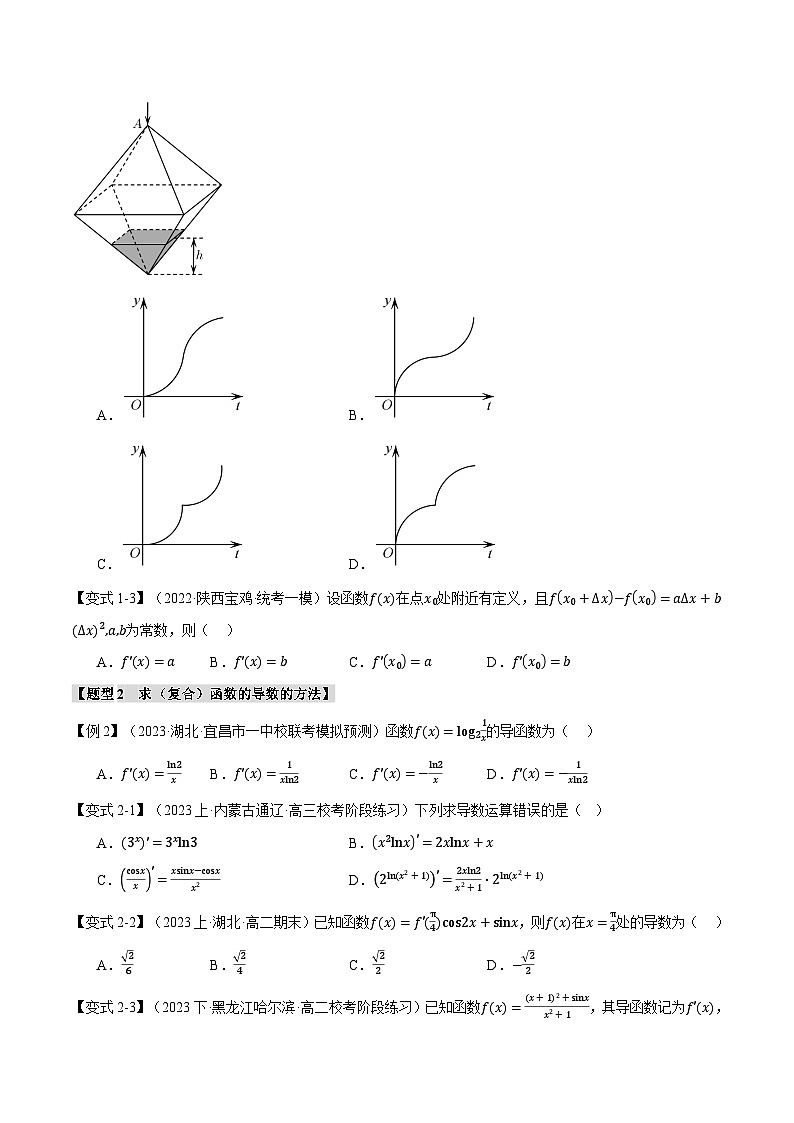
【变式1-2】（2022·安徽合肥·合肥校考模拟预测）如图所示，连接棱长为2cm的正方体各面的中心得到一个多面体容器，从顶点A处向该容器内注水，直至注满水为止.已知顶点B到水面的距离h以每秒1cm的速度匀速上升，设该容器内水的体积Vcm3与时间t(s)的函数关系是Vt，则函数y=Vt的图象大致是（ ）
A．B．
C．D．
【变式1-3】（2022·陕西宝鸡·统考一模）设函数fx在点x0处附近有定义，且fx0+Δx−fx0=aΔx+bΔx2,a,b为常数，则（ ）
A．f′x=aB．f′x=bC．f′x0=aD．f′x0=b
【题型2 求（复合）函数的导数的方法】
【例2】（2023·湖北·宜昌市一中校联考模拟预测）函数f(x)=lg21x的导函数为（ ）
A．f′(x)=ln2xB．f′(x)=1xln2C．f′(x)=−ln2xD．f′(x)=−1xln2
【变式2-1】（2023上·内蒙古通辽·高三校考阶段练习）下列求导数运算错误的是（ ）
A．(3x)′=3xln3B．x2lnx′=2xlnx+x
C．csxx′=xsinx−csxx2D．2ln(x2+1)′=2xln2x2+1⋅2ln(x2+1)
【变式2-2】（2023上·湖北·高二期末）已知函数f(x)=f′(π4)cs2x+sinx，则fx在x=π4处的导数为（ ）
A．26B．24C．22D．−22
【变式2-3】（2023下·黑龙江哈尔滨·高二校考阶段练习）已知函数fx=x+12+sinxx2+1，其导函数记为f′x，则f389+f′389+f−389−f′−389=（ ）
A．2B．−2C．3D．−3
【题型3 求曲线切线的斜率（倾斜角）】
【例3】（2023·河北唐山·模拟预测）已知曲线fx=2xcsx在x=0处的切线为l，则l的斜率为（ ）
A．ln2B．−ln2C．1D．−1
【变式3-1】（2023·新疆阿克苏·校考一模）若直线y=kx+n与曲线y=lnx+1x相切，则k的取值范围是（ ）
A．−∞,14B．4,+∞C．−4,+∞D．14,+∞
【变式3-2】（2023·内蒙古赤峰·校联考一模）函数y=fx在P1,f1处的切线如图所示，则f1+f′1=（ ）
A．0B．12C．32D．-12
【变式3-3】（2023·贵州·校联考模拟预测）设点P是函数fx=x3−12f′1x+f′2图象上的任意一点，点P处切线的倾斜角为α，则角α的取值范围是（ ）
A．0,3π4B．0,π2∪3π4,πC．π2,3π4D．0,π2∪3π4,π
【题型4 求在曲线上一点的切线方程、过一点的切线方程】
【例4】（2023·江苏连云港·校考模拟预测）曲线y=x3+1在点a,2处的切线方程为（ ）
A．y=3x+3B．y=3x−1
C．y=−3x−1D．y=−3x−3
【变式4-1】（2023下·辽宁·高二校联考阶段练习）过原点且与函数fx=ln−x图像相切的直线方程是（ ）
A．y=−xB．y=−2exC．y=−1exD．y=−ex
【变式4-2】（2023·陕西咸阳·校考模拟预测）已知函数fx=1ex−1，则曲线y=fx在点−1,f−1处的切线方程为（ ）
A．ex+y+1=0B．ex−y+1=0
C．ex+y−1=0D．ex−y−1=0
【变式4-3】（2023·全国·高三专题练习）已知函数fx=x3−x2+2x+1，则曲线y=fx过坐标原点的切线方程为（ ）
A．y=xB．y=2xC．y=3xD．y=4x
【题型5 已知切线（斜率）求参数】
【例5】（2023·重庆·统考三模）已知直线y＝ax－a与曲线y=x+ax相切，则实数a＝（ ）
A．0B．12C．45D．32
【变式5-1】（2023·河南郑州·统考二模）已知曲线y=xlnx+ae−x在点x=1处的切线方程为2x−y+b=0，则b=（ ）
A．－1B．－2C．－3D．0
【变式5-2】（2023·全国·校联考模拟预测）已知函数fx=ax2+blnx的图象在点1,f1处的切线方桯为y=3x−1.则a−b的值为（ ）
A．1B．2C．3D．4
【变式5-3】（2023·全国·高三专题练习）已知曲线y=axex+lnx在点1,ae处的切线方程为y=3x+b，则（ ）
A．a=e，b=−2B．a=e，b=2
C．a=e−1，b=−2D．a=e−1，b=2
【题型6 切线的条数问题】
【例6】（2023·全国·高三专题练习）已知函数fx=−x3+3x，则过点−3,−9可作曲线y=fx的切线的条数为（ ）
A．0B．1C．2D．3
【变式6-1】（2023·全国·模拟预测）若曲线y=1−xex有两条过点Aa,0的切线，则a的取值范围是（ ）
A．−∞,−1∪3,+∞B．−3,1
C．−∞,−3D．−∞,−3∪1,+∞
【变式6-2】（2023·全国·模拟预测）若过点P(m,0)与曲线f(x)=x+1ex相切的直线只有2条，则m的取值范围是（ ）
A．(−∞,+∞)B．(−∞,−3)∪(1,+∞)
C．(−1,3)D．(−∞,−1)∪(3,+∞)
【变式6-3】（2023上·湖北·高三鄂南高中校联考期中）函数f(x)=x3+(a−1)x2−x+b为R上的奇函数，过点P−12,1作曲线y=f(x)的切线，可作切线条数为（ ）
A．1B．2C．3D．不确定
【题型7 两条切线平行、垂直、重合（公切线）问题】
【例7】（2023·陕西渭南·统考一模）已知直线y=ax+b(a∈R,b>0)是曲线fx=ex与曲线gx=lnx+2的公切线，则a+b等于（ ）
A．e+2B．3C．e+1D．2
【变式7-1】（2023上·陕西·高三校联考阶段练习）函数fx=x−alnx在区间1,6的图象上存在两条相互垂直的切线，则a的取值范围（ ）
A．1,6B．1,3C．3,4D．4,6
【变式7-2】（2023·全国·模拟预测）已知函数fx=lnx与gx的图象关于直线y=x对称，直线l与gx,ℎx=ex+1−1的图象均相切，则l的倾斜角为（ ）
A．π6B．π4C．π3D．3π4
【变式7-3】（2023·海南·海南华侨中学校考一模）若对函数fx=2x−sinx的图象上任意一点处的切线l1，函数gx=mex+m−2x的图象上总存在一点处的切线l2，使得l1⊥l2，则m的取值范围是（ ）